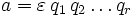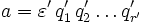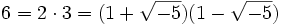Gaußscher Ring

Ein faktorieller Ring (auch ZPE-Ring oder Gaußscher Ring) ist eine algebraische Struktur, und zwar ein Integritätsring, in dem jedes Element 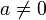$a \neq 0$ eine eindeutige Zerlegung in irreduzible Faktoren besitzt (Achtung: ein faktorieller Ring ist etwas anderes als ein Faktorring!).

Definition

Ein Integritätsring A heißt faktoriell (englisch: UFD, unique factorization domain), wenn er die folgende Eigenschaft besitzt:

• Jedes Element 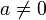$a\ne0$, das keine Einheit ist, besitzt eine im Wesentlichen eindeutige Zerlegung in irreduzible Faktoren.

Für einen Integritätsring ist die Eigenschaft, faktoriell zu sein, äquivalent zur Eigenschaft, ein ZPE-Ring (Zerlegung in Primelemente) zu sein:

• Jedes Element 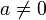$a\ne0$, das keine Einheit ist, besitzt eine Zerlegung in ein Produkt von Primelementen, ggf. multipliziert mit einer Einheit. (Darstellungen als Produkt von Primelementen sind stets im Wesentlichen eindeutig.)

Zerlegung in irreduzible Faktoren

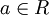$a \in R$ hat eine Zerlegung in irreduzible Faktoren, wenn a eine Darstellung

$a=\varepsilon\, q_1\, q_2 \dots q_r$

mit einer Einheit $\varepsilon$ und irreduziblen Elementen q_i hat. Diese Zerlegung ist im Wesentlichen eindeutig, wenn bei jeder weiteren solchen Darstellung

$a=\varepsilon'\, q_1'\, q_2' \dots q_{r'}'$

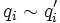gilt: r = r' und $q_i \sim q_i'$ (nach eventuellem Umnummerieren).

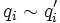$q_i \sim q_i'$ bedeutet: q_i und q_i' sind assoziiert.

Eigenschaften

• Irreduzible Elemente in faktoriellen Ringen sind prim. (Damit folgt auch die Äquivalenz der oben angegebenen Beschreibungen.)

Beispiele

• Jeder nullteilerfreie Hauptidealring ist ein faktorieller Ring. Beispiele sind der Ring 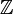$\Bbb Z$ der ganzen Zahlen sowie der Polynomring K[X] in einer Veränderlichen über einem Körper K.
• Polynomringe und Ringe formaler Potenzreihen über einem Körper
• Polynomringe über einem faktoriellen Ring sind wieder faktoriell (Satz von Gauß, siehe Inhalt (Polynom))
• reguläre lokale Ringe

Gegenbeispiele

Ein Beispiel für einen Ring, in dem es eine Zerlegung in irreduzible Elemente gibt, die nicht eindeutig ist, ist der Ring $\mathbb Z[\sqrt{-5}]$ (siehe Adjunktion): In den beiden Produktdarstellungen

$6=2\cdot 3=(1+\sqrt{-5})(1-\sqrt{-5})$

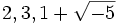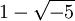sind die Faktoren jeweils irreduzibel, aber unter den vier Zahlen $2,3,1+\sqrt{-5}$ und $1-\sqrt{-5}$ sind keine zwei assoziiert. Die Einheiten in diesem Ring sind + 1 und − 1.

Ein Beispiel für einen Ring, in dem eine Zerlegung in irreduzible Elemente nicht immer existiert, diese aber eindeutig ist, wann immer sie existiert ist der Ring der holomorphen Funktionen auf einem Gebiet U in der komplexen Ebene $\mathbb{C}$ (mit punktweiser Addition und Multiplikation): Dieser Ring ist nullteilerfrei (das folgt aus dem Identitätssatz für holomorphe Funktionen. Die Einheiten sind genau die holomorphen Funktionen ohne Nullstellen (also z.B. die komplexe Exponentialfunktion). Die irreduziblen Elemente sind bis auf Einheiten genau die Funktionen der Form (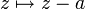$z\mapsto z-a$) für einen Punkt 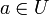$a\in U$. Daraus folgt, dass eine holomorphe Funktion genau dann ein Produkt aus irreduziblen Elementen ist, wenn sie nur endlich viele Nullstellen hat. Da es aber auf jedem Gebiet auch holomorphe Funktionen gibt mit unendlich vielen Nullstellen, ist dieser Ring kein faktorieller Ring. Falls eine holomorphe Funktion allerdings eine solche Darstellung hat, so ist diese im wesentlichen eindeutig, weil die irreduziblen Elemente alle prim sind.