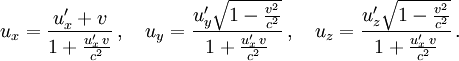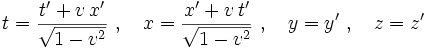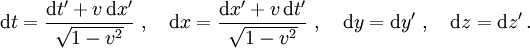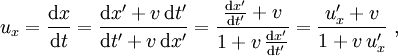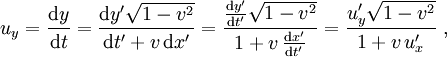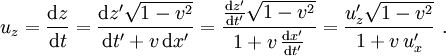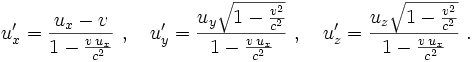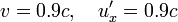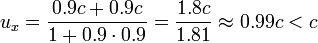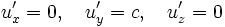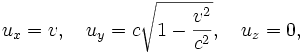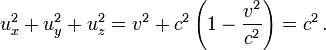Relativistische Geschwindigkeitsaddition

In der klassischen Physik werden Geschwindigkeiten vektoriell addiert. Da in der speziellen Relativitätstheorie gegeneinander bewegte Inertialsysteme durch Lorentztransformationen miteinander zusammenhängen, werden zwei Geschwindigkeiten anders zur Gesamtgeschwindigkeit zusammengesetzt:

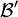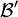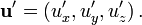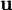Ein Beobachter $\mathcal{B}^\prime$ bewege sich gegenüber dem Beobachter $\mathcal{B}$ mit der Geschwindigkeit v in Richtung der x-Achse. Für den Beobachter $\mathcal{B}^\prime$ bewege sich ein Körper mit der Geschwindigkeit $\mathbf u^\prime=(u^\prime_x,u^\prime_y,u^\prime_z)\,.$ Dann hat dieser Körper für den Beobachter $\mathcal{B}$ die Geschwindigkeit $\mathbf u$ mit Komponenten

$u_x=\frac{u_x'+v}{1+\frac{u_x'\,v}{c^2}}\,,\quad u_y=\frac{u_y'\sqrt{1-\frac{v^2}{c^2}}}{1+\frac{u_x'\,v}{c^2}}\,,\quad u_z=\frac{u_z'\sqrt{1-\frac{v^2}{c^2}}}{1+\frac{u_x'\,v}{c^2}}\,.$

Sind die beteiligten Geschwindigkeiten sehr klein gegenüber der Lichtgeschwindigkeit, so unterscheiden sich sowohl der Nenner als auch der Term unter der Wurzel kaum von 1, und es ergibt sich in guter Näherung die übliche nichtrelativistische Geschwindigkeitsaddition. Beispielsweise ist die von einem am Bahndamm stehenden Beobachter gemessene Geschwindigkeit einer Person, die durch einen Zug mit 200 km/h in Bewegungsrichtung des Zuges mit 5 km/h relativ zum Zug läuft, gerade mal um 0,17 nm/h langsamer als die bei einfacher Addition erhaltenen 205 km/h. Zum Vergleich: Der Durchmesser eines Atoms liegt in der Größenordnung von 0.1 nm. Das heißt, der „Zugläufer“ kommt in der Stunde knapp 2 Atomdurchmesser weniger weit, als man es bei nichtrelativistischer Rechnung erwarten würde – was bei einer zurückgelegten Strecke von 205 km sicher vernachlässigbar ist.

Für Geschwindigkeiten nahe der Lichtgeschwindigkeit ergeben sich jedoch deutliche Abweichungen von der nichtrelativistischen Additionsregel.

Herleitung

Um das Formelbild einfach zu halten, verwenden wir als Längeneinheit die Strecke, die Licht in einer Sekunde zurückgelegt und nennen sie eine Lichtsekunde. Dann haben Zeit und Länge dieselbe Maßeinheit und die dimensionslose Lichtgeschwindigkeit beträgt 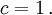$c=1\,.$ Untersuchungen in anderen Maßsystemen bringen keine tieferen Einsichten.

Aus der inversen Lorentz-Transformation (Ersatz von v durch -v)

$t = \frac{t' + v\, x'}{\sqrt{1 - v^2}}\ ,\quad x =\frac{x' + v\,t'}{\sqrt{1 - v^2}} \ ,\quad y = y'\ ,\quad z = z'$

folgt, da die Transformation linear ist, für die Differentiale

$\mathrm{d}t = \frac{\mathrm{d}t' + v\,\mathrm{d}x'}{\sqrt{1 - v^2}}\ ,\quad \mathrm{d}x = \frac{\mathrm{d}x' + v\,\mathrm{d}t'}{\sqrt{1 -v^2}}\ ,\quad \mathrm{d}y = \mathrm{d}y'\ ,\quad \mathrm{d}z = \mathrm{d}z'\,.$

Daher folgt für die Geschwindigkeiten, die der Beobachter $\mathcal{B}$ ermittelt,

$u_x=\frac{\mathrm{d}x}{\mathrm{d}t} = \frac{\mathrm{d}x' + v\,\mathrm{d}t'}{\mathrm{d}t' + v\, \mathrm{d}x'} = \frac{\frac{\mathrm{d}x'}{\mathrm{d}t'} + v} {1 + v\, \frac{\mathrm{d}x'}{\mathrm{d}t'}} = \frac{u_x' + v}{1 + v\, u_x'}\ ,$

$u_y=\frac{\mathrm{d}y}{\mathrm{d}t} = \frac{\mathrm{d}y'\sqrt{1 - v^2}}{\mathrm{d}t' + v\, \mathrm{d}x'} = \frac{\frac{\mathrm{d}y'}{\mathrm{d}t'}\sqrt{1 - v^2}} {1 + v\, \frac{\mathrm{d}x'}{\mathrm{d}t'}} = \frac{u_y'\sqrt{1 -v^2}}{1 + v\, u_x'}\ ,$

$u_z=\frac{\mathrm{d}z}{\mathrm{d}t} = \frac{\mathrm{d}z'\sqrt{1 - v^2}}{\mathrm{d}t' + v\, \mathrm{d}x'} = \frac{\frac{\mathrm{d}z'}{\mathrm{d}t'}\sqrt{1 - v^2}} {1 + v\, \frac{\mathrm{d}x'}{\mathrm{d}t'}} = \frac{u_z'\sqrt{1 -v^2}}{1 + v\, u_x'}\ .$

Umgekehrt gilt (Ersetzen von v durch -v, mit allen Faktoren c)

$u_x'= \frac{u_x - v}{1 - \frac{v\, u_x}{c^{2}}}\ , \quad u_y'= \frac{u_y\sqrt{1 - \frac{v^2}{c^2}}}{1 - \frac{v\, u_x}{c^{2}}}\ , \quad u_z'= \frac{u_z\sqrt{1 - \frac{v^2}{c^2}}}{1 - \frac{v\, u_x}{c^{2}}}\ .$

Folgerungen

Als Folge dieses Additionstheorems kann auch durch Überlagerung zweier Geschwindigkeiten die Lichtgeschwindigkeit nicht übertroffen werden.

Es sei

$v=0.9c,\quad u_x'=0.9c$

Dann ist

$u_x = \frac{0.9c+0.9c}{1+0.9\cdot 0.9} = \frac{1.8c}{1.81} \approx 0.99c < c$

und nicht etwa 1.8c.

Ist die Geschwindigkeit 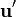$\mathbf u^\prime$ für den Beobachter 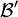$\mathcal{B}^\prime$ gleich der Lichtgeschwindigkeit, dann ist sie es auch für den Beobachter $\mathcal{B}$

Ist zum Beispiel

$u_x'=0,\quad u_y'=c,\quad u_z'=0$

dann ist

$u_x=v,\quad u_y=c\sqrt{1-\frac{v^2}{c^2}},\quad u_z=0,$

also insbesondere

$u_x^2 + u_y^2 + u_z^2 = v^2 + c^2\left(1-\frac{v^2}{c^2}\right) = c^2\,.$

Weblinks