- Ringerweiterung
-
Als Ringerweiterung werden solche chemische Reaktionen bezeichnet, die einen vorhandenen Ring um ein Glied oder mehrere Glieder erweitern. Dies geschieht meist über ein kationisches Intermediat. Die Ringerweiterung ist das Gegenstück zur Ringverengung (z. B. der Favorskii-Umlagerung).
Reaktionen
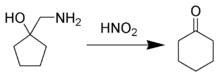
Bekannte Ringerweiterungsreaktionen sind zum Beispiel die Beckmann-Umlagerung, die Tiffeneau-Ringerweiterung und die Baeyer-Villiger-Reaktion.[1]
Die Beckmann-Umlagerung, bei der zyklische Ketone zu Lactamen umgelagert werden, ist hierbei die industriell bedeutendste. Sie wird zur Synthese von ε-Caprolactam einem Grundstoff zur Polyamid-Herstellung genutzt. Die peroxidische Baeyer-Villiger-Reaktion dient zur Lactonisierung zyklischer Ketone. Bei der Tiffeneau-Reaktion wird in zyklische Ketone formal eine Methylengruppe insertiert.
Einzelnachweise
- ↑ Römpp CD 2006, Georg Thieme Verlag 2006.
Wikimedia Foundation.