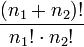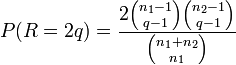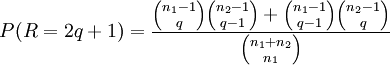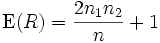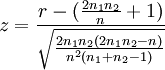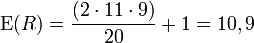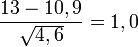- Runs-Test
-
Der Run- oder Runs-Test (auch Wald-Wolfowitz-Test, nach Abraham Wald und Jacob Wolfowitz, Iterationstest oder Geary-Test) ist ein nichtparametrischer Test auf Zufälligkeit einer Folge. Konzeptionell wird von einer dichotomen Grundgesamtheit, also einem Urnenmodell mit zwei Sorten Kugeln, ausgegangen. Es sind n viele Kugeln entnommen worden. Es soll die Hypothese geprüft werden, dass die Entnahme zufällig erfolgt ist.
Inhaltsverzeichnis
Vorgehensweise
Es wurden einer dichotomen Grundgesamtheit n Kugeln entnommen. Die Ergebnisse liegen in ihrer chronologischen Abfolge vor. Es werden nun alle benachbarten Ergebnisse gleicher Ausprägung zu einem Lauf oder Run zusammengefasst. Wenn die Folge tatsächlich zufällig ist, sollten nicht zu wenig Runs vorliegen, aber auch nicht zu viele.
Es wird die Hypothese aufgestellt: Die Entnahme erfolgte zufällig.
Für die Festlegung der Zahl der Runs, bei der die Hypothese abgelehnt wird, wird die Verteilung der Runs benötigt: Es seien n1 die Zahl der Kugeln erster Sorte und n2 = n - n1 der zweiten Sorte; es sei r die Zahl der Runs. Nach dem Symmetrieprinzip ist die Wahrscheinlichkeit für jede beliebige Folge der Kugeln bei zufälliger Entnahme gleich groß. Es gibt insgesamt
Möglichkeiten der Entnahme.
Bezüglich der Verteilung der Zahl der Runs unterscheidet man die Fälle:
1. Die Zahl der Runs r ist geradzahlig:
- Es liegen
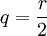 Runs der Kugeln der ersten Sorte und
Runs der Kugeln der ersten Sorte und 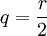 Runs der Kugeln der zweiten Sorte vor. Die Wahrscheinlichkeit, dass genau r Runs eingetreten sind, ist dann
Runs der Kugeln der zweiten Sorte vor. Die Wahrscheinlichkeit, dass genau r Runs eingetreten sind, ist dann
2. Die Zahl der Runs r ist ungeradzahlig:
- Es liegen
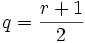 Runs der Kugeln der ersten Sorte und
Runs der Kugeln der ersten Sorte und 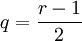 Runs der Kugeln der zweiten Sorte vor oder der umgekehrte Fall. Die Wahrscheinlichkeit, dass genau r Runs eingetreten sind, berechnet sich dann als Summe aus diesen beiden Möglichkeiten
Runs der Kugeln der zweiten Sorte vor oder der umgekehrte Fall. Die Wahrscheinlichkeit, dass genau r Runs eingetreten sind, berechnet sich dann als Summe aus diesen beiden Möglichkeiten
Ist r zu klein oder zu groß, führt das zur Ablehnung der Nullhypothese. Bei einem Signifikanzniveau von alpha wird H0 abgelehnt, wenn für die Prüfgröße r gilt:
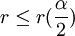 oder
oder 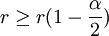
mit r(p)als Quantil der Verteilung von R an der Stelle p, wobei hier das Prinzip des konservativen Testens angewendet wird. Da die Berechnung der kritischen Werte von r für die Ablehnung der Hypothese umständlich ist, bedient man sich häufig einer Tabelle.
Einfaches Beispiel
Für eine Podiumsdiskussion mit zwei politischen Parteien wurden die Sprecher angeblich zufällig ermittelt. Es wurde ausgelost, dass von der Partei Supi 4 Vertreter und von der Partei Toll 5 Vertreter in der folgenden Reihe sprechen dürfen:
S S T S T T T S T
Ein Vertreter von Toll beschwerte sich, dass S vorgezogen würde. Es wurde ein Run-Test vorgenommen:
Es ist n1 = 4 und n2 = 5. Man erhielt r = 6 Runs.
Nach der Tabelle des Run-Testes wird H0 abgelehnt, wenn r ≤ 2 oder r ≥ 9 ist. Also liegt die Prüfgröße r = 6 im Nichtablehnungsbereich; man kann nach den Kriterien des Run-Testes davon ausgehen, dass die Reihenfolge der Sprecher zufällig ist.
Ergänzungen
Parameter der Verteilung von R
Der Erwartungswert von R ist
und die Varianz
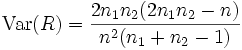 .
.
Grundgesamtheit mit mehr als zwei Ausprägungen des Merkmals
Liegt eine endliche Folge reeller Zahlen (xi) eines metrischen Merkmals vor, wird die Folge dichotomisiert: Man bestimmt zunächst den Median z der Folge. Werte xi < z werden dann als Kugeln der ersten Sorte, Werte xi > z als Kugeln der zweiten Sorte interpretiert. Die entstandene dichotome Folge kann dann wieder auf Zufälligkeit getestet werden (siehe Beispiel unten).
Liegt eine nichtnumerische Symbolsequenz mit mehr als zwei Ausprägungen vor, muss zunächst eine numerische Reihe erzeugt werden, wobei hier das Problem bestehen kann, dass die Symbole nicht geordnet werden können.
Normalapproximation
Für Stichprobenumfänge n1,n2 > 20 ist die Zahl der Runs R annähernd normalverteilt mit Erwartungswert und Varianz wie oben. Man erhält die standardisierte Prüfgröße
Die Hypothese wird abgelehnt, wenn
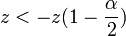 oder
oder 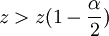
mit
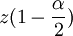 als Quantil der Standardnormalverteilung für die Wahrscheinlichkeit
als Quantil der Standardnormalverteilung für die Wahrscheinlichkeit 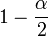 .
.Anwendungen
Der Runtest kann angewendet werden, um Stationarität bzw. Nicht-Korrelation in einer Zeitreihe oder anderen Sequenz zu überprüfen, vor allem wenn die Verteilung des Merkmals unbekannt ist. Die Nullhypothese ist hier, dass aufeinanderfolgende Werte unkorreliert sind.
Der Run-Test kann mit dem Chi-Quadrat-Test kombiniert werden, da beide Prüfgrößen asymptotisch unabhängig voneinander sind.
Beispiel für ein metrisches Merkmal
Es liegt die Folge
13 3 14 14 1 14 3 8 14 17 9 14 13 2 16 1 3 12 13 14
vor. Sie wird mit dem Median z = 13 dichotomisiert. Für die erste Ausprägung wird + gesetzt, für die zweite Ausprägung -.
0 -10 1 1 -12 1 -10 -5 1 4 -4 1 0 -11 3 -12 -10 -1 0 1
+ - + + - + - - + + - + + - + - - - + +
Man erhält bei n1 = 11 (+) und n2 = 9 (-) r = 13 Runs. R ist annähernd normalverteilt mit dem Erwartungswert
und der Varianz
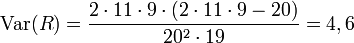 .
.
Die Prüfgröße z errechnet sich dann als
Bei einem Signifikanzniveau von 0,05 wird H0 abgelehnt, wenn |z| > 1,96. Dies ist nicht der Fall.
Entscheidung: Die Hypothese wird nicht abgelehnt. Die Elemente der Stichprobe sind vermutlich zufällig entnommen worden.
Literatur
- James V. Bradley: Distribution-Free Statistical Tests, 1968, Chapter 12, ISBN 0132162598
- Herbert Büning, Götz Trenkler: Nichtparametrische statistische Methoden, 1999, Kapitel 4.5, ISBN 3-11-016351-9
Siehe auch
Autokorrelation, Zufallszahlengenerator, Pseudozufallszahlen, Trend, Median, Varianz
Weblinks
Wikimedia Foundation.