Schauder-Basis

In der Funktionalanalysis wird eine abzählbare Menge {b_n} eines Banachraums, deren lineare Hülle dicht im ganzen Raum ist, als Schauderbasis bezeichnet, falls jeder Vektor bezüglich ihr eine eindeutige Darstellung als (unendliche) Linearkombination hat.

Benannt sind die Schauderbasen nach dem polnischen Mathematiker Juliusz Schauder (1899–1943), der sie 1927 beschrieb.

Definition

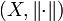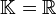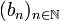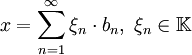Sei $(X, \left\|\cdot\right\|)$ ein Banachraum über dem Grundkörper $\mathbb{K} = \mathbb{R}$ oder $\mathbb{C}$. Eine Folge $(b_n)_{n\in\mathbb{N}}$ in X heißt Schauderbasis, falls jedes $x \in X$ eindeutig als konvergente Reihe $x = \sum_{n=1}^{\infty} \xi_n \cdot b_n, \; \xi_n \in \mathbb{K}$, dargestellt werden kann.

Beispiele

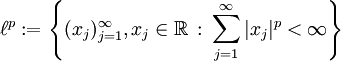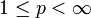• Im Folgenraum $\ell^p := \left\{ (x_j)_{j=1}^\infty, x_j \in \mathbb{R} \,:\, \sum_{j=1}^\infty |x_j|^p < \infty \right\}$ mit der Norm $\left\| x \right\| = \sqrt[p]{\sum_{j=1}^\infty |x_j|^p}$ bilden für $1 \leq p < \infty$ die Einheitsvektoren 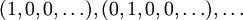$(1, 0, 0, \dots), (0,1,0,0, \dots), \dots$ eine Schauderbasis.

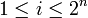• Setze h₁(x) = 1 für alle $x\in [0,1]$, und für $1\le i\le 2^n$ definiere $h_{2^n+i}:[0,1]\rightarrow \R$ durch

$h_{2^n+i}(x)=\begin{cases}1,&(2i-2)/2^{n+1} \le x < (2i-1)/2^{n+1},\\-1,&(2i-1)/2^{n+1} \le x < 2i/2^{n+1},\\0&\mbox{sonst}.\end{cases}$

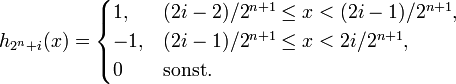
Bis auf einen konstanten Faktor ist jedes h_k eine auf [0,1) eingeschränkte Haar-Wavelet-Funktion. Man kann zeigen, dass die Folge 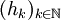$(h_k)_{k\in\mathbb{N}}$, die man nach Alfréd Haar auch das Haar-System nennt, eine Schauderbasis für L^p([0,1]) ist, $1\le p < \infty$.

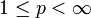Eigenschaften

Allgemeine Eigenschaften

• Ein Banachraum, der eine Schauderbasis besitzt, ist separabel.
• Umgekehrt besitzt nicht jeder separable Banachraum eine Schauderbasis.^[1]
• Banachräume mit Schauderbasis haben die Approximationseigenschaft.
• In unendlichdimensionalen Banachräumen ist eine Schauderbasis nie Hamelbasis des Vektorraums, da eine solche in unendlichdimensionalen Banachräumen stets überabzählbar sein muss (siehe Satz von Baire).
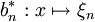• Die Darstellung eines Elements $x \in X$ bezüglich einer Schauderbasis ist nach Definition eindeutig. Die Zuordnungen $b_n^\ast : x \mapsto \xi_n$ werden als Koeffizientenfunktionale bezeichnet; sie sind linear und stetig und daher Elemente des Dualraums von X.

Eigenschaften der Basis

Schauderbasen können weitergehende Eigenschaften haben. Die Existenz von Schauderbasen mit solchen Eigenschaften hat dann weitere Konsequenzen für den Banachraum.

Ist 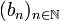$(b_n)_{n\in\mathbb{N}}$ eine Schauderbasis des Banachraums X, so gibt es eine Konstante K > 0, so dass für p < q und jede Wahl von Skalaren 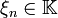$\xi_n\in {\mathbb K}$ die Ungleichung 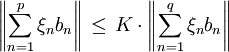$\left\|\sum_{n=1}^p \xi_nb_n\right\| \, \le \, K\cdot \left\|\sum_{n=1}^q \xi_nb_n\right\|$ gilt. Das Infimum über die K > 0, die zu vorgegebener Basis diese Ungleichung erfüllen, nennt man die Basiskonstante. Man spricht von einer monotonen Basis, wenn die Basiskonstante gleich 1 ist.

Man nennt eine Basis 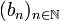$(b_n)_{n\in\mathbb{N}}$ beschränkt vollständig (englisch: boundedly complete), wenn es zu jeder Folge 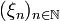$(\xi_n)_{n\in\mathbb{N}}$ von Skalaren mit 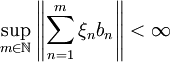$\sup_{m \in \N}\left\| \sum_{n=1}^m \xi_nb_n\right\|&amp;lt;\infty$ ein $x\in X$ gibt mit $x = \sum_{n=1}^\infty \xi_nb_n$.

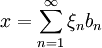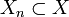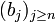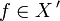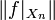Weiter sei $X_n\subset X$ der von $(b_j)_{j\ge n}$ erzeugte abgeschlossene Unterraum, und für $f\in X\,'$ sei $\|f|_{X_n}\|$ die Norm des eingeschränkten Funktionals 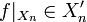$f|_{X_n} \in X_n'$. Die Basis heißt schrumpfend (englisch: shrinking), wenn 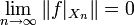$\lim_{n\to\infty}\|f|_{X_n}\| = 0$ für alle $f\in X\,'$.

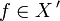Schließlich spricht man von einer unbedingten Basis (englisch: unconditional), wenn alle Reihen 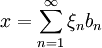$x=\sum_{n=1}^\infty \xi_nb_n$ in den Entwicklungen bezüglich der Basis unbedingt konvergieren. Man kann zeigen, dass das Haar-System in L^p([0,1]) für 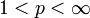$1&amp;lt;p&amp;lt;\infty$ eine unbedingte Basis ist, nicht aber für p = 1. Der Raum L¹([0,1]) besitzt keine unbedingte Basis.

Zwei Sätze von R. C. James

Die folgenden beiden Sätze von Robert Clarke James zeigen die Bedeutung der Basisbegriffe.

• R. C. James: Sei X ein Banachraum mit Schauderbasis. X ist genau dann reflexiv, wenn die Basis beschränkt vollständig und schrumpfend ist.

Für unbedingte Schauderbasen kann man das Vorhandensein gewisser Unterräume charakterisieren. Sei X ein Banachraum mit unbedingter Schauderbasis. Dann gilt:

• X enthält keinen zu c₀ isomorphen Unterraum. 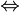$\Leftrightarrow$ Die Basis ist beschränkt vollständig.
• X enthält keinen zu 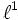$\ell^1$ isomorphen Unterraum. 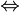$\Leftrightarrow$ Die Basis ist schrumpfend.

Als Konsequenz ergibt sich daraus:

• R. C. James: Sei X ein Banachraum mit unbedingter Schauderbasis. X ist genau dann reflexiv, wenn X keinen zu c₀ oder 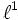$\ell^1$ isomorphen Unterraum enthält.

Literatur

• Bernard Beauzamy: Introduction to Banach Spaces and their Geometry, Elesevier Science Publishers (1985) ISBN 0444878785
• Zdzisław Denkowski, Stanisław Migórski, Nikolas S. Papageorgiou: An introduction to nonlinear analysis. Kluwer, Boston 2003, ISBN 0-306-47392-5
• Joseph Diestel: Sequences and Series in Banach Spaces. 1984, ISBN 0-387-90859-5.
• Yuli Eidelman, Vitali Milman, Antonis Tsolomitis: Functional analysis. An introduction. American Mathematical Society, Providence 2004, ISBN 0821836463
• Ivan Singer: Bases in Banach spaces I (1970) und Bases in Banach spaces II (1981), Springer Verlag

Einzelnachweise

1. ↑ Per Enflo: A counterexample to the approximation problem in Banach spaces. Acta Mathematica, Band 130, Nr. 1, Juli 1973.