- Sedezimal
-
Hexadezimalziffern,
binär und dezimal:Hex. Dualsystem Dez. 0 0 0 0 0 00 1 0 0 0 1 01 2 0 0 1 0 02 3 0 0 1 1 03 4 0 1 0 0 04 5 0 1 0 1 05 6 0 1 1 0 06 7 0 1 1 1 07 8 1 0 0 0 08 9 1 0 0 1 09 A 1 0 1 0 10 B 1 0 1 1 11 C 1 1 0 0 12 D 1 1 0 1 13 E 1 1 1 0 14 F 1 1 1 1 15 Im Hexadezimalsystem (lat.-griech. Mischwort) werden Zahlen in einem Stellenwertsystem zur Basis 16 dargestellt.
Alternative Bezeichnungen für hexadezimal (von griech. "hexa" und lat. "decem") sind hexadekadisch (Griechisch) und sedezimal (Latein) (Falsch hingegen ist der Ausdruck hexagesimal, der synonym zu sexagesimal ist und das Zahlensystem zur Basis 60 bezeichnet.).
In der Datenverarbeitung wird das Hexadezimalsystem sehr oft verwendet, da es sich hierbei letztlich nur um eine komfortablere Verwaltung des Binärsystems handelt. Die Datenworte bestehen in der Informatik meist aus Oktetten, die statt als achtstellige Binärzahlen auch als nur zweistellige Hexadezimalzahlen dargestellt werden können. Im Gegensatz zum Dezimalsystem eignet sich das Hexadezimalsystem mit seiner Basis als vierte Zweierpotenz (16 = 24) zur einfacheren Notation der Binärzahlen, da stets eine feste Anzahl Zeichen zur Wiedergabe des Datenwortes benötigt wird.
In den 1960er und 1970er Jahren wurde in der Informatik häufig auch das Oktalsystem mit seiner Basis als dritte Zweierpotenz (8 = 23) verwendet, da es mit den üblichen Ziffern von 0 bis 7 auskommt. Heute gilt es wegen seiner Einbindung von nur jeweils drei Bits als überholt.
Wir sind es gewöhnt, im Dezimalsystem zu rechnen. Das bedeutet, unser indo-arabisches Zahlensystem verwendet zehn Symbole zur Notation der Ziffern (0 bis 9). Das Hexadezimalsystem enthält dagegen sechzehn Ziffern. Seit Mitte der 1950er Jahre werden zur Darstellung der sechs zusätzlichen Ziffern die Buchstaben A bis F oder a bis f als Zahlzeichen verwendet. Dies geht auf die damalige Praxis der IBM-Informatiker zurück.
Inhaltsverzeichnis
Darstellung von Hexadezimalzahlen
Um hexadekadische von dekadischen Zahlen unterscheiden zu können, existieren mehrere Schreibweisen. Üblicherweise werden hexadekadische mit einem Index oder Präfix versehen.
Verbreitete Schreibweisen sind: 7216, 72hex, 72h, 72H, 0x72, "72, $72 und X'72' wobei das Präfix 0x und das Suffix h insbesondere in der Programmierung und technischen Informatik Verwendung finden. Die Schreibweise mit dem Dollar-Präfix ist in den Assemblersprachen bestimmter Prozessorfamilien üblich, zum Beispiel beim Motorola 68xx und 68xxx oder beim MOS 65xx; die Schreibweise X'72' ist in der Welt der IBM-Großrechner üblich.
Der Übersicht dienende Trennpunkte können bei Hexadezimalzahlen alle vier Stellen gesetzt werden, trennen also Gruppen von jeweils sechzehn Bit. Die Bedeutung der 1.000016 = 65.53610 unter den hexadekadischen Zahlen entspricht also jener der 1.00010 unter den dekadischen.
Zum Vergleich ein voller Vierundsechzig-Bit-Bus mit und ohne Trennpunkte: FFFF.FFFF.FFFF.FFFF und FFFFFFFFFFFFFFFF
Dezimale Zahlen werden, wo sie nicht der zu erwartende Normalfall sind, indiziert: 11410
Zählen im Hexadezimalsystem
Gezählt wird wie folgt:
0 1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F 20 21 22 23 24 25 26 27 28 29 2A 2B 2C 2D 2E 2F ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 FA FB FC FD FE FF ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... FF0 FF1 FF2 FF3 FF4 FF5 FF6 FF7 FF8 FF9 FFA FFB FFC FFD FFE FFF ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... FFF0 FFF1 FFF2 FFF3 FFF4 FFF5 FFF6 FFF7 FFF8 FFF9 FFFA FFFB FFFC FFFD FFFE FFFF ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... Für die hexadezimalen Ziffern und Zahlen sind keine eigenständigen Namen gebräuchlich. Hexadezimalzahlen werden daher Ziffer für Ziffer gelesen.
Beispiele:
- 1F sprich: „eins-eff“,
- F112 sprich: „eff-eins-eins-zwei“.
Hexadezimalbrüche
Da das Hexadezimalsystem ein Stellenwertsystem ist, haben die Stellen nach dem Komma (das auch hier manchmal als Beistrich, manchmal als Punkt geschrieben wird) den Stellenwert
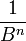 , wobei B die dezimale Basis 16 und n die Position der jeweiligen Nachkommastelle ist. Die erste Nachkommastelle (n=1) hat damit den Stellenwert
, wobei B die dezimale Basis 16 und n die Position der jeweiligen Nachkommastelle ist. Die erste Nachkommastelle (n=1) hat damit den Stellenwert 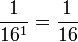 , die zweite Nachkommastelle (n=2) hat den Stellenwert
, die zweite Nachkommastelle (n=2) hat den Stellenwert 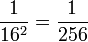 , die dritte Nachkommastelle (n=3) hat den Wert
, die dritte Nachkommastelle (n=3) hat den Wert 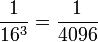 und so weiter.
und so weiter.Da die Zahl 16 nur über den einzigen Primfaktor 2 verfügt, sind Perioden eher die Regel:

= 1 
= 0,316 
= 0,1C716 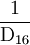
= 0,13B16 
= 0,816 
= 0,2A16 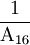
= 0,1916 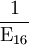
= 0,124916 
= 0,516 
= 0,24916 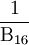
= 0,1745D16 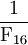
= 0,116 
= 0,416 
= 0,216 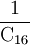
= 0,1516 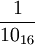
= 0,116 Anwendung
Informatik
Das Hexadezimalsystem eignet sich sehr gut, um Folgen von Bits (verwendet in der Digitaltechnik) darzustellen. Vier Stellen einer Bitfolge (ein Nibble, auch Tetrade) werden wie eine Dualzahl interpretiert und entsprechen so einer Ziffer des Hexadezimalsystems, da 16 die vierte Potenz von 2 ist. Die Hexadezimaldarstellung der Bitfolgen ist leichter zu lesen und schneller zu schreiben:
Binär Hexadezimal Dezimal 1111 = F = 15 1.1111 = 1F = 31 11.0111.1100.0101 = 37C5 = 14.277 1010.1100.1010.1011 = ACAB = 44.203 1.0000.0000.0000.0000 = 1.0000 = 65.536 1010.1111.1111.1110.0000.1000.0001.0101 = AFFE.0815 = 2.952.661.013
Computersoftware stellt daher Maschinensprache oft auf diese Weise dar.
Mathematik
Seit die Bailey-Borwein-Plouffe-Formel zur Berechnung von π im Jahr 1995 entwickelt wurde, ist das Hexadezimalsystem auch jenseits der Informatik von Bedeutung. Diese Summenformel kann jede beliebige Hexadezimalstelle von π berechnen, ohne die vorhergehenden Stellen dafür zu brauchen.
Konvertierung in andere Zahlensysteme
Umwandlung von Dezimalzahlen in Hexadezimalzahlen
Eine Möglichkeit, eine Zahl des Dezimalsystems in eine Zahl des Hexadezimalsystems umzurechnen, ist die Betrachtung der Divisionsreste, die entstehen, wenn die Zahl durch die Basis 16 geteilt wird.
Im Beispiel der 127810 sähe das so aus:
1278 : 16 = 79 Rest: 14 (= E) (Nr:1278-(79*16)=14) 79 : 16 = 4 Rest: 15 (= F) (Nr:79-(4*16)=15) 4 : 16 = 0 Rest: 4 (Nr:4-(0*16)=4)
Die Hexadezimalzahl wird von unten nach oben gelesen und ergibt somit 4.F.E.
Umwandlung von Hexadezimalzahlen in Dezimalzahlen
Um eine Hexadezimalzahl in eine Dezimalzahl umzuwandeln, muss man die einzelnen Ziffern mit der jeweiligen Potenz der Basis multiplizieren. Der Exponent der Basis entspricht der Stelle der Ziffer, wobei der Zahl vor dem Komma eine Null zugeordnet wird. Dazu muss man allerdings noch die Ziffern A, B, C, D, E, F in die entsprechenden Dezimalzahlen 10, 11, 12, 13, 14, 15 umwandeln.
Beispiel für 4FE16:
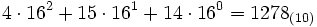
Für das Zählen und Rechnen im Hexadezimalsystem gibt es eine Eselsbrücke: A = 10 und B = 11 kann sich jeder merken. C wie zwölf, D wie dreizehn, E für vierzehn kommt vor F wie fünfzehn.
Umwandlung Hexadezimal nach Oktal
Um Zahlen zwischen dem vor allem früher in der Informatik verbreiteten Oktalsystem und dem heute gebräuchlichen Hexadezimalsystem vorzunehmen, ist es zweckmäßig, den Zwischenschritt über das Binärsystem zu gehen. Dies gelingt recht einfach, da sowohl die Basis 8, als auch die Basis 16 Zweierpotenzen sind.
- Die Hexadezimalzahl wird nach obiger Tabelle in eine Folge von Binärziffern umgewandelt.
- Die Vierergruppen in Dreiergruppen umwandeln.
- Anschließend wird die Binärfolge in eine Oktalfolge übersetzt.
Beispiel für 8D5316:
8D5316 = 1000.1101.0101.00112 = 1'000'110'101'010'0112 = 1065238
Umwandlung Oktal nach Hexadezimal
Genauso einfach erfolgt die Umwandlung von oktal nach hexadezimal, nur dass hier der Weg
- Oktalfolge → Binärfolge in Dreiergruppen → Binärfolge in Vierergruppen → Hexadezimalfolge
lautet.
Mathematische Darstellung des Hexadezimalsystems
Formuliert im Dezimalsystem:
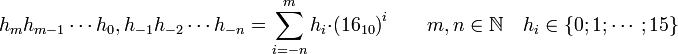
Formuliert im Hexadezimalsystem:
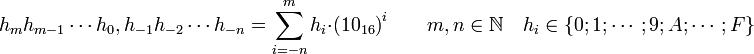
Siehe auch
Weblinks
- Online-Umrechner für Dezimal-/Hexadezimalzahlen (JavaScript, GPL)
- Zahlensysteme im Vergleich
- SPIEGEL ONLINE mit einem historischen mechanischen Taschenrechner für das Hexadezimalsystem
Wikimedia Foundation.
