Semidefinit

Definitheit ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Er beschreibt, welche Vorzeichen reelle quadratische Formen annehmen können, die durch Matrizen oder allgemeiner durch Bilinearformen erzeugt werden.

Definitheit von Bilinearformen und Sesquilinearformen

Es sei V ein Vektorraum über den reellen (oder komplexen) Zahlen.

Eine symmetrische Bilinearform 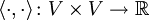$\langle{\cdot}, {\cdot}\rangle\colon V\times V\to\mathbb R$ (bzw. eine hermitesche Sesquilinearform 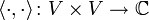$\langle{\cdot}, {\cdot}\rangle\colon V\times V\to \mathbb{C}$) heißt

positiv definit,	falls 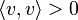$\langle v,v\rangle>0$
positiv semidefinit,	falls 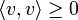$\langle v,v\rangle\geq0$
negativ definit,	falls 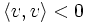$\langle v,v\rangle<0$
negativ semidefinit,	falls 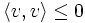$\langle v,v\rangle\leq0$

jeweils für alle 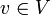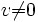$v\in V$, $v\not=0$, gilt. Man beachte, dass auch im komplexen Fall wegen der geforderten Hermiteizität 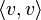$\langle v,v\rangle$ stets reell ist.
Trifft keine dieser Bedingungen zu, heißt die Form indefinit. Genau in diesem Fall nimmt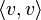 $\langle v,v\rangle$ sowohl positive als auch negative Werte an.

Die obigen Bedingungen bedeuten also, dass die zugehörige quadratische Form 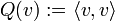$Q(v) := \langle v,v\rangle$ positiv definit, positiv semidefinit, negativ definit, negativ semidefinit bzw. indefinit ist.

Gelegentlich werden diese Begriffe auch für beliebige, nicht notwendig symmetrische Bilinearformen (bzw. hermitesche Sesquilinearformen) eingeführt. Im komplexen Fall muss man dann zusätzlich fordern, dass für alle 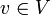$v\in V$ der Wert 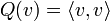$Q(v) = \langle v,v\rangle$ reell ist.

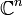Beispielsweise ist das Standard-Skalarprodukt auf dem $\R^n$ (bzw. $\mathbb C^n$) positiv definit.

• Siehe auch: Skalarprodukt

Definitheit von Matrizen

Jede quadratische Matrix beschreibt eine Bilinearform auf 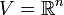$V = \R^n$ (bzw. eine Sesquilinearform auf 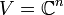$V = \C^n$). Man nennt eine quadratische Matrix deshalb positiv definit, wenn diese Eigenschaft auf die durch die Matrix definierte Bilinearform bzw. Sesquilinearform zutrifft. Entsprechend definiert man auch die anderen Eigenschaften. Dies bedeutet: Eine beliebige (ggf. symmetrische bzw. hermitesche) n×n-Matrix A ist

positiv definit,	falls xTAx > 0
positiv semidefinit,	falls 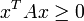$x^TAx \geq 0$
negativ definit,	falls xTAx < 0
negativ semidefinit,	falls 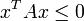$x^TAx \leq 0$

für alle n-zeiligen Spaltenvektoren x ≠ 0.

Im komplexen Fall muss der Vektor x auf der linken Seite zum Zeilenvektor transponiert und zusätzlich komplex-konjugiert werden (hermitesch Adjungiertes, 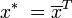$x^*\; = \overline x^T$ statt lediglich 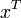$x^T\;$). Beschränkt man sich hier nicht auf hermitesche Matrizen, so muss man in diesem Fall zusätzlich voraussetzen, dass x ^* Ax stets reell ist (im hermiteschen Fall ist das automatisch erfüllt).

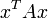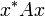Eine Matrix, die weder positiv noch negativ semidefinit ist, nennt man „indefinit“. Genau dann nimmt $x^TAx\;$ (bzw. $x^*Ax\;$) sowohl positive als auch negative Werte an.

Positiv definite Matrizen entstehen beispielsweise bei der Beschreibung von Systemen, die auf dem Energieerhaltungssatz basieren. ^[1]

Es gibt daneben weitere äquivalente Definitionen von Definitheit.

Symmetrischer Anteil

Eine quadratische Matrix A ist genau dann positiv definit, wenn ihr symmetrischer (bzw. hermitescher) Teil

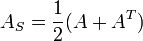$A_S = \frac{1}{2} (A + A^T)$ bzw. $A_H = \frac{1}{2} (A + A^*)$

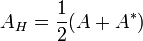
positiv definit ist. Dabei bezeichnet 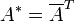$A^* = \overline A^T$ die hermitesch adjungierte Matrix.

Eigenwerte

Eine quadratische symmetrische (bzw. hermitesche) Matrix ist

positiv definit,	falls alle Eigenwerte größer als Null sind;
positiv semidefinit,	falls alle Eigenwerte größer oder gleich Null sind;
negativ definit,	falls alle Eigenwerte kleiner als Null sind;
negativ semidefinit,	falls alle Eigenwerte kleiner oder gleich Null sind und
indefinit,	falls positive und negative Eigenwerte existieren.

Damit kann jedes Verfahren zur Bestimmung oder Abschätzung von Eigenwerten benutzt werden, um die Definitheit der Matrix zu bestimmen. Eine Möglichkeit sind die Gerschgorin-Kreise, die es erlauben das Spektrum zumindest abzuschätzen. Dies reicht häufig schon aus, um die Definitheit zu bestimmen. Die Gerschgorin-Kreise geben anhand der Einträge der Matrix Mengen in der komplexen Ebene an, in denen die Eigenwerte enthalten sind, im Falle von symmetrischen Matrizen Intervalle auf der reellen Achse. Damit ist es manchmal einfach möglich, die Definitheit einer Matrix zu bestimmen. Einzelheiten hierzu, insbesondere über die Signatur von symmetrischen Bilinearformen und Matrizen, siehe Trägheitssatz von Sylvester.

Hauptminoren

Eine symmetrische bzw. hermitesche Matrix A ist genau dann positiv definit, wenn alle Hauptminoren von A positiv sind. Entsprechend ist A negativ definit, falls alle Hauptminoren von − A positiv sind. A ist also genau dann negativ definit, falls die Vorzeichen der Hauptminoren alternieren, d. h., falls alle ungeraden Hauptminoren negativ sind und alle geraden positiv.

Bemerkungen

• Für Semidefinitheit gibt es kein Hauptminorenkriterium.^[2]

• Für nicht-hermitesche Matrizen gilt das Kriterium nicht. Ein Beispiel dafür ist die indefinite Matrix 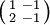$\left(\begin{smallmatrix}1 & -1\\ 2 & -1\end{smallmatrix}\right)$, deren Hauptminoren alle positiv sind.

• Das Kriterium wird auch oft Sylvester-Kriterium genannt. Vereinzelt wird auch die Bezeichnung „Hurwitz-Kriterium“ verwendet, obwohl sich dieses ursprünglich nur auf Hurwitz-Matrizen bezog.

Gaußsches Eliminationsverfahren

Eine quadratische Matrix 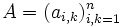$A=(a_{i,k})_{i,k=1}^n$ ist genau dann positiv definit, wenn der gaußsche Eliminationsprozess bei Diagonalstrategie mit n positiven Pivotelementen durchgeführt werden kann. Diese Bedingung eignet sich vor allem für Fälle, in denen sowieso das gaußsche Eliminationsverfahren angewandt werden muss.

Cholesky-Zerlegung

Eine symmetrische Matrix A ist genau dann positiv definit, wenn es eine Cholesky-Zerlegung gibt mit

A = GG^T,

wobei G die Form

$G=\begin{pmatrix} g_{11} & 0 & 0 & \cdots & 0\\ g_{21} & g_{22} & 0 & \cdots & 0\\ g_{31} & g_{32} & g_{33} & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ g_{n1} & g_{n2} & g_{n3} & \cdots & g_{nn} \end{pmatrix}$

hat.

Bedeutung

• Die Einschränkung einer positiv definiten Bilinear- bzw. Sesquilinearform auf einen Unterraum ist wieder positiv definit, insbesondere also nicht ausgeartet. Diese Tatsache ermöglicht die Zerlegung eines Raumes in einen Unterraum und dessen orthogonales Komplement.
• Definitheit spielt bei der Untersuchung von kritischen Stellen einer Funktion 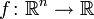$f\colon\R^n\to\R$, also der Extremwertberechnung, eine entscheidende Rolle.

Einzelnachweise

1. ↑ Norbert Köckler, Hans Rudolf Schwarz: Numerische Mathematik. Teubner, Stuttgart/Leipzig/Wiesbaden 2004, ISBN 3-519-42960-8, S. 58
2. ↑ IEEE: On Sylvester's Criterion for Positive-Semidefinite Matrices, Transaction on automatic control, Juni 1973, englisch