Backus-Normalform

Die Backus-Naur-Form oder Backus-Normalform, kurz BNF, ist eine kompakte formale Metasprache zur Darstellung kontextfreier Grammatiken (Typ-2-Grammatiken in der Chomsky-Hierarchie). Hierzu zählt die Syntax gängiger höherer Programmiersprachen. Sie wird auch für die Notation von Befehlssätzen und Kommunikationsprotokollen verwendet.

Ursprünglich war sie nach John Backus benannt, später wurde sie (auf Anregung von Donald E. Knuth) auch nach Peter Naur benannt. Beide waren Informatikpioniere, die sich mit der Erstellung der Algol-60-Regeln und insbesondere mit der Kunst des Compilerbaus beschäftigten. Durch die Backus-Naur-Form im Algol 60 Report wurde es erstmals möglich, die Syntax einer Programmiersprache formal exakt, also ohne die Ungenauigkeiten natürlicher Sprachen, darzustellen.

Es gibt viele Varianten der Backus-Naur-Form. Die erweiterte Backus-Naur-Form (EBNF) ist eine gebräuchliche Variante, die unter anderem eine kompakte Notation von sich wiederholenden Elementen erlaubt. Für Syntaxdefinitionen in Internetnormen wird überwiegend die angereicherte Backus-Naur-Form (ABNF) verwendet.

Grundlagen

Ein Programm besteht zunächst aus sichtbaren, also auf der Tastatur vorhandenen, Zeichen. Daneben treten noch Leerzeichen und Zeilentrenner auf. Die sichtbaren Zeichen werden zu den Terminalsymbolen (engl. terminals) gerechnet.

BNF verwendet so genannte Ableitungsregeln (Produktionen), in denen Nichtterminalsymbole (engl. nonterminals) definiert werden. Dabei dient das Zeichen | (vertikaler Strich) als Alternative, die Zeichenfolge ::= wird zur Definition verwendet und die Nichtterminalsymbole, die auch syntaktische Variablen genannt werden, werden mit spitzen Klammern <…> umschlossen:

Alternative:

<Ziffer außer Null> ::= 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

Eine Ziffer außer Null ist also entweder eine 1 oder eine 2 oder eine 3 usw. Es lassen sich auch Terminalfolgen definieren, also eine Sequenz. Als Elemente dürfen Terminalsymbole und Nichtterminalsymbole auftreten:

Sequenz:

<Ziffer>              ::= 0 | <Ziffer außer Null> 
<Zweistellige Zahl>   ::= <Ziffer außer Null> <Ziffer>
<Zehn bis Neunzehn>   ::= 1 <Ziffer>
<Zweiundvierzig>      ::= 42

Eine Ziffer ist also eine 0 oder eine Ziffer außer Null. Eine zweistellige Zahl ist eine Ziffer außer Null gefolgt von einer Ziffer. Zweiundvierzig ist eine 4 gefolgt von einer 2.

Wiederholungen müssen in BNF über Rekursionen definiert werden. Eine Ableitungsregel kann dazu auf der rechten Seite das Symbol auf der linken Seite enthalten, etwa:

 <Ziffernfolge> ::= <Ziffer> | <Ziffer> <Ziffernfolge>

Lies: Eine Ziffernfolge ist eine Ziffer oder eine Ziffer gefolgt von einer Ziffernfolge.

Eine Ziffernfolge passt also zu den Symbolfolgen 0, 1, 2, 10, 9870, 8970635 usw., jedoch auch zu 00, 000, …. Eine positive Zahl darf nicht mit 0 beginnen. Dies leistet die folgende Regel:

 <Positive Zahl> ::= <Ziffer außer Null> | <Ziffer außer Null> <Ziffernfolge>

BNF und Programmiersprachen

Um die Syntax von Programmiersprachen wie ALGOL, Pascal oder Java in BNF darzustellen, müssen auch die Schlüsselwörter (IF, SWITCH) zu den Terminalsymbolen gerechnet werden. In einem Compiler werden sie in einer Vorphase, der lexikalischen Analyse, erkannt und als besondere Zeichen weitergegeben. Kommentare werden von der lexikalischen Analyse erkannt (und oft entfernt), manchmal auch weitere Elemente wie Gleitkommazahlen, Bezeichner und Zeichenketten.

Damit lässt sich die gesamte Syntax z. B. eines PASCAL-Programms in BNF darstellen (teilweise gekürzt):

<Programm>               ::= 'PROGRAM' <Bezeichner> 'BEGIN' <Satzfolge> 'END' .
<Bezeichner>             ::= <Buchstabe> <Restbezeichner>
<Restbezeichner>         ::= | <Buchstabe oder Ziffer> <Restbezeichner>
<Buchstabe oder Ziffer>  ::= <Buchstabe> | <Ziffer>
<Buchstabe>              ::= A | B | C | D | … | Z | a | b | … | z   *)
<Ziffer>                 ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
<Satzfolge>              ::= …
…

Eine Syntaxanalyse besteht aus der Rückführung eines Programmtexts auf das Nichtterminalsymbol <Programm>. Ein Programm muss also mit dem Wort PROGRAM beginnen, auf das ein Bezeichner folgt. Bezeichner beginnen mit einem Buchstaben, gefolgt von beliebig vielen Buchstaben oder Ziffern.

Die Rückführung auf <Programm> gelingt bei

 PROGRAM Ggt BEGIN … END.

 PROGRAM DiesisteinlangerBezeichnermit123 BEGIN … END .

nicht jedoch bei

 Ggt BEGIN … END.         (beginnt nicht mit PROGRAM)

 PROGRAM 123 BEGIN … END. (123 ist kein Bezeichner, Bezeichner müssen mit einem Buchstaben beginnen)

Beispiel

Hier eine BNF für eine deutsche Postanschrift:

 <Post-Anschrift>  ::= <Personenteil> <Straße> <Stadt>
 <Personenteil>    ::= [ <Titel> ] <Namensteil> <EOL>
 <Vornamenteil>    ::= <Vorname> | <Initial> . 
 <Namensteil>      ::= <Vornamenteil> <Nachname> | <Vornamenteil> <Namensteil>
 <Straße>          ::= <Straßenname> <Hausnummer> <EOL>
 <Stadt>           ::= <Postleitzahl> <Stadtname> <EOL>

(Definition von Straßenname, Hausnummer etc. fehlen)

Die Ausformulierung lautet:

• Eine Postanschrift besteht aus einem Personenteil, gefolgt von einer Straße, gefolgt von der Stadt.
• Der Personenteil besteht aus einem optionalen Titel und einem Namensteil, gefolgt von einem Zeilenende.
• Der Vornamenteil besteht aus einem Vornamen oder einem Initial, auf den ein Punkt folgt.
• Der Namensteil besteht aus einem Vornamensteil, einem Nachnamen oder aus einem Vornamensteil und wiederum aus einem Namensteil. (Diese Regel zeigt die Benutzung von Rekursion in BNFs und stellt den Fall dar, dass eine Person mehrere Vornamen und/oder Initialen besitzt.)
• Eine Straße besteht aus einem Straßenname, gefolgt von einer Hausnummer, gefolgt von einem Zeilenende.
• Eine Stadt besteht aus einer Postleitzahl, gefolgt von einem Stadtname, gefolgt von einem Zeilenende.

Man beachte, dass einiges (wie die Postleitzahl oder Hausnummer) nicht weiter spezifiziert ist. Es wird angenommen, dass diese lexikalischen Details vom Kontext abhängen oder anderweitig spezifiziert sind.

Dieses Beispiel ist keine reine Form aus dem ALGOL 60 report. Die eckigen Klammern […] stellen eine Option dar. Sie wurden einige Jahre später in der Definition von IBMs PL/I eingeführt, sind aber allgemein anerkannt.

Option:

<Zahl> ::= [ - ] <Positive Zahl>

Das Minuszeichen ist optional. Die Definition ist äquivalent zu

<Zahl> ::=  <Positive Zahl> | - <Positive Zahl>

Eine Zahl ist eine positive Zahl, oder ein Minuszeichen, gefolgt von einer positiven Zahl.

Modifikationen der BNF

Syntaxdiagramme der modifizierten BNF.

Die Alternative und die Sequenz sind zur Darstellung der BNF grundsätzlich geeignet. Allerdings lassen sich die Zeichen |, [, ] nicht von den BNF-Zeichen unterscheiden. Oft können auch Zeichen wie Punkt oder Minus nur schwer erkannt werden.

Die BNF wird daher in der Regel etwas modifiziert und ergänzt:

• Keine spitzen Klammern <…> für Nichtterminale.
• Zeichen als Terminalsymbole werden in Anführungszeichen gesetzt ("0" | "1" …)
• Nichtterminalsymbole in Kleinbuchstaben.
• Schlüsselwörter in Großbuchstaben.
• Nur = statt ::=.
• Ein Punkt am Ende einer Regel. Mehrzeilige Regeln sind möglich.

 ziffer           = "0" | "1" | "2" | "3" | … | "9" .
 zifferaußernull  = "1" | "2" | "3" | … | "9" .
 ziffernfolge     = ziffer | ziffer ziffernfolge .
 zahl             = [ "-" ] zifferaußernull [ ziffernfolge ] | "0" .
 programm         = PROGRAM bezeichner 
                    BEGIN satzfolge END "." .

Die Option wird manchmal nicht mit eckigen Klammern, sondern durch ein angefügtes Fragezeichen dargestellt. Die Wiederholung durch Rekursion ist oft umständlich:

• Optionen werden durch ein angefügtes Fragezeichen dargestellt.
• Wiederholungen (ein- oder mehrfach) werden durch ein angefügtes Pluszeichen dargestellt.
• Optionale Wiederholungen (keinmal, ein- oder mehrfach) werden durch einen angefügten Stern dargestellt.
• Klammern dienen zur Gruppierung

 ziffernfolge ::= ziffer+ .
 zahl         ::= ( "-" )? zifferaußernull ( ziffernfolge )? | "0" .
 bezeichner   ::= buchstabe ( buchstabe | ziffer )* .

Die erweiterte Backus-Naur-Form geht andere Wege. Sie verwendet eckige Klammern […] für die Option, jedoch geschweifte Klammern {…} für die optionale Wiederholung. Terminale und Nichtterminale werden nicht streng unterschieden. Hier würde das obenstehende Beispiel so dargestellt:

 Ziffernfolge = Ziffer { Ziffer } ;
 Zahl         = [ "-" ] ZifferAußerNull [ Ziffernfolge ] | "0" ;
 Bezeichner   = Buchstabe { Buchstabe | Ziffer } ;

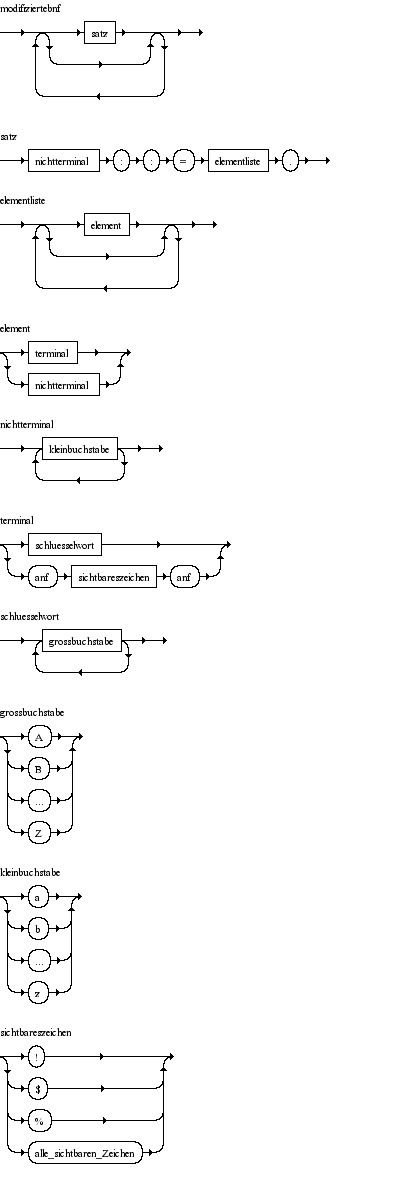
Selbstdefinition einer (modifizierten) BNF

Eine modifizierte BNF kann sich selbst definieren:

 modifiziertebnf   ::= | satz modifiziertebnf .
 satz              ::= nichtterminal ":" ":" "=" elementliste "." .
 elementliste      ::= | element elementliste .
 element           ::= terminal | nichtterminal .
 nichtterminal     ::= kleinbuchstabe | kleinbuchstabe nichtterminal .
 terminal          ::= schluesselwort | anf sichtbareszeichen anf . 
 schluesselwort    ::= grossbuchstabe | grossbuchstabe schluesselwort .
 anf               ::= """ .
 grossbuchstabe    ::= "A" | "B" | … | "Z" .
 kleinbuchstabe    ::= "a" | "b" | … | "z" .
 sichtbareszeichen ::= "!" | "$" | "%" | … (alle sichtbaren Zeichen) .

Bei dieser Version werden Schlüsselwörter als Großbuchstaben dargestellt, Nichtterminale als Kleinbuchstaben. Wiederholungen müssen über Rekursionen definiert werden. Davon wird in der eigenen Definition auch Gebrauch gemacht (modifiziertebnf, elementliste, nichtterminal, schlüsselwort).

BNF und Parser-Generatoren

Manche Parsergeneratoren verwenden eine eigene Form der BNF als Eingabe und generieren hieraus einen Parser für die zugrundegelegte Programmiersprache.

Das dem Betriebssystem Unix beiligende Programm yacc ist so ein Programm. Es generiert einen tabellengesteuerten Parser aus einer BNF-Definition, wobei nur Produktionen (: statt ::=) und Alternativen (|) zulässig sind. Dies ist notwendig, da yacc eine S-Attribution ermöglicht, einem optionalen Teil jedoch kein sinnvoller semantischer Typ des Attributs zugeordnet werden kann. Als Ausgabe erhält man ein Unterprogramm in der Programmiersprache C. Die zugrundegelegte Grammatik muss dabei die LALR-Eigenschaft erfüllen.

Literatur

• Donald E. Knuth: Backus Normal Form versus Backus Naur Form, Communications of the ACM 7 (December 1964), S. 735f. – DOI 10.1145/355588.365140

Weblinks

• Revised Report on the Algorithmic Language Algol 60 (englisch)
• Vergleich der BNF-Varianten (englisch)
• Erzeugen von Syntaxdiagrammen aus EBNF
• RFC 5234: Definition der ABNF (englisch)

Siehe auch

• Formale Sprache
• Syntaxbaum
• Erweiterte Backus-Naur-Form