Produktion (Grammatik)

Eine Produktionsregel (auch Regel oder Produktion genannt) ist ein geordnetes Paar (P,Q) der beiden Wörter P und Q, welches besagt, dass bei der Erzeugung einer formalen Sprache aus einer gegebenen formalen Grammatik mit dieser Produktionsregel die Zeichenfolge P durch Q ersetzt werden kann. Das Wort P wird Prämisse und das Wort Q Konklusion der Regel (P,Q) genannt. Dabei ist P ein Wort, welches sowohl aus Terminalsymbolen, als auch aus Nichtterminalsymbolen besteht, welches aber mindestens ein nichtterminales Symbol besitzen muss. Q hingegen ist ein beliebiges aus Terminalen und Nichtterminalen bestehendes Wort, welches auch das leere Wort sein kann. Eine Regel (P,Q) wird oftmals durch die Schreibweise 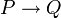$P \rightarrow Q$ dargestellt und eine Menge von Regeln 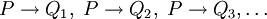$P \rightarrow Q_1,\; P \rightarrow Q_2,\; P \rightarrow Q_3, \ldots$ kann durch die Schreibweise 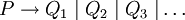$P \rightarrow Q_1 \;|\; Q_2 \;|\; Q_3 \;| \ldots$ abgekürzt werden. Produktionsregeln sind grundlegende Bestandteile einer formalen Grammatik, mit deren Hilfe in der Informatik sowie in der Linguistik formale Sprachen beschrieben werden können.

Beispiele

Es sei innerhalb einer formalen Grammatik mit den Nichtterminalsymbolen N = {A,B} und den Terminalsymbolen T = {a,b} die Produktionsregel 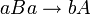$aBa \rightarrow bA$ definiert. Durch Anwendung dieser Regel kann bei der Erzeugung der durch die Grammatik beschriebenen Sprache zum Beispiel das Wort aBaBaBA in das Wort bABaBA abgeleitet werden, wobei hier das Präfix aBa durch die Konklusion bA ersetzt wird. Es wäre jedoch nach der Definition formaler Grammatiken auch möglich, das zweite Vorkommen der Zeichenfolge aBa zu ersetzen, so dass das Wort aBbABA entsteht.

Wäre außerdem die Regel 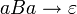$aBa \rightarrow \varepsilon$ definiert, so könnte das zuvor betrachtete Wort aBaBaBA außerdem in die Wörter BaBA bzw. aBBA abgeleitet werden ($\varepsilon$ ist die in der Regel verwendete Notation für das leere Wort).

Informatik

Wie bereits beschrieben, stellen Produktionsregeln einen grundlegenden Bestandteil formaler Grammatiken dar und werden demnach dazu verwendet, um formale Sprachen zu beschreiben. So werden Produktionsregel etwa im Rahmen des Compilerbaus dazu verwendet, um eine Programmiersprache zu beschreiben. Produktionsregeln werden hier häufig in der Backus-Naur-Form dargestellt.

Eine kognitive Anwendung haben Produktionsregeln in regelbasierten Systemen: Hier spricht man von Produktionsregeln, wenn die Konklusionen der Regeln, mit denen das System arbeitet, nur aus Konjunktionen von Literalen bestehen.

Linguistik

In der Theorie der Transformationsgrammatik veranschaulichen Produktionsregeln, die hier Phrasenstrukturregeln (PS-Regeln) genannt werden, den Gedanken, dass ein Satz allmählich durch Umwandlung einer Tiefenstruktur in eine Oberflächenstruktur entstehe.

Die ersten und klassisch gewordenen PS-Regeln in Chomskys Buch "Strukturen der Syntax" lauten:

S -> NP VP (ein Satz besteht aus einer Nominalphrase und einer Verbalphrase)
VP -> V NP*　(eine Verbalphrase besteht aus einem Verb und null bis vielen Nominalphrasen)

Die zweite Regel illustriert laut Chomsky die Kreativität von Sprache. Mit einer Regel können viele (unendliche) Kombinationen von Texten erzeugt werden. Dies erkläre, warum Kleinkinder noch nie gehörte Sätze sagen können; in einer Universalgrammatik seien diese Regeln nämlich schon angeboren.