Shefferscher Strich

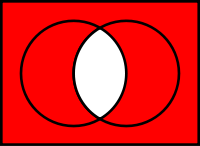Venn-Diagramm von A | B
Die Sheffer-Funktion ist die Negation des logischen und.
Im rot markierten Bereich ist die Funktion wahr, also genau da, wo und falsch ist.

Der Sheffersche Strich (auch Sheffer stroke, Sheffer-Strich, Sheffer-Funktion oder Sheffer-Operator nach Henry Maurice Sheffer genannt) bzw. NAND (engl. not and = nicht und), geschrieben als „|“, bezeichnet in der Booleschen Algebra und der Aussagenlogik einen booleschen Operator bzw. Junktor.

Die damit begründete logische Operation ist äquivalent zur Negation der Konjunktion (AND-Verknüpfung) zweier boolescher Variablen, umgangssprachlich entspricht dies dem „nicht beide“.

Definition

Semantische Definition (Wahrheitstabelle)

Der Sheffersche Strich, bezeichnet durch "|" (oder manchmal auch als "↑", "NAND", "$\overline{\land}$"), ist ein zweistelliger Junktor der Aussagenlogik, der semantisch durch die folgende Wahrheitstabelle definiert wird (hierbei steht w für wahr, f für falsch):

A	B	A | B
w	w	f
w	f	w
f	w	w
f	f	w

Die Gesamtaussage zweier durch den Shefferschen Strich verknüpften Aussagen ist wahr, wenn mindestens eine Aussage falsch ist, bzw. dann falsch, wenn beide wahr sind.

Syntaktische Definition

Der Sheffersche Strich kann durch die Negation der Konjunktion definiert werden:

A | B$:= \neg (A \wedge B) \equiv \overline{A \wedge B}$

Geschichte

Der Sheffersche Strich ist nach Henry Maurice Sheffer benannt, der bewies,^[1] dass die üblichen Junktoren der Aussagenlogik, nämlich Negation, Konjunktion, Disjunktion, Konditional usw. durch ihn ausgedrückt werden können. Charles Sanders Peirce hatte diese Tatsache mehr als dreißig Jahre vorher gefunden, aber nie veröffentlicht. Peirce erkannte auch, dass sich alle Junktoren außerdem durch den zum Shefferschen Strich dualen Operator, der Peirce-Funktion, NOR, ausdrücken lassen.

Äquivalenzen

Die üblichen Junktoren der Aussagenlogik lassen sich wie folgt durch den Shefferschen Strich ausdrücken:

Negation (Komplement-Gatter): $\neg A \equiv A | A,$

Konjunktion (Und-Gatter): $A \wedge B \equiv (A | B) | (A | B),$

Disjunktion (Oder-Gatter): $A \vee B \equiv (A | A) | (B | B),$

materiale Implikation, Konditional: $A \rightarrow B \equiv A | (B | B) \equiv A | (A | B)$

materiale Äquivalenz, Bikonditional (XNOR, XNOR-Gatter): $A \leftrightarrow B \equiv (A|B)|((A|A)|(B|B))$

Kontravalenz, Antivalenz, Alternative (XOR, XOR-Gatter): $A\;\dot\or\;B \equiv (A|(A|B))|(B|(A|B))$

Eigenschaften und Besonderheiten

Der Sheffersche Strich hat die Besonderheit, dass er allein, ohne weitere logische Operatoren, ein für die Aussagenlogik funktional vollständiges Junktorensystem bildet. Diese Eigenschaft ist die Grundlage für die große Bedeutung des NAND in der modernen digitalen Elektronik.

Die NAND-Verknüpfung sowie alle anderen logischen Verknüpfungen können durch NAND-Gatter respektive deren Verschaltung umgesetzt werden und gelten in der Digitaltechnik daher als Standardbaustein. Zudem werden NAND-Bausteine häufig benutzt, da sie die günstigsten digitalen Bausteine sind. So werden sehr platzsparend etwa Speicherbausteine wie NAND-Flashes aus NAND-Bausteinen aufgebaut.

Literatur

• Charles Sanders Peirce: A Boolean Algebra with One Constant. In: C. Hartshorne, P. Weiss (Hrsg.): The Simplest Mathematics. Harvard University Press, 1880 (Collected Papers. Band 4), S. 12-20..
• Henry Maurice Sheffer: A set of five independent postulates for Boolean algebras, with application to logical constants. In: Transactions of the American Mathematical Society. 14, 1913, S. 481-488.

Einzelnachweise

1. ↑ H. M. Sheffer: A set of five independent postulates for Boolean algebras, with application to logical constants. In: Transactions of the American Mathematical Society. 14, 1913, S. 481-488.

Weblinks

• http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/nand.html
• implementations of 2 and 4-input NAND gates
• Proofs of some axioms by Stroke function by Yasuo Setô @ Project Euclid