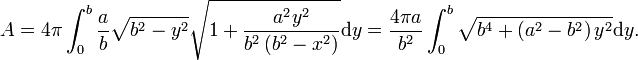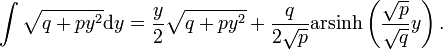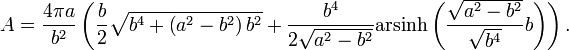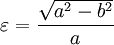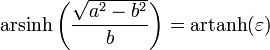- Sphäroid
-
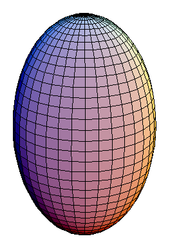
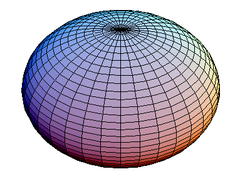
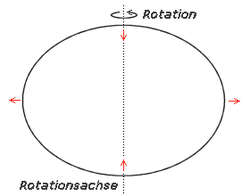
Abgeplattetes Rotationsellipsoid Verlängertes Rotationsellipsoid Ein Rotationsellipsoid (auf Englisch "spheroid") ist ein Ellipsoid, das durch die Drehung einer Ellipse um eine ihrer Achsen entsteht. Im Gegensatz zu einem allgemeinen Ellipsoid sind zwei Achsen gleich lang. Man unterscheidet dabei je nach Länge der Drehachse das
- verlängerte (prolate) Ellipsoid bei Rotation um die große Halbachse a und das
- abgeplattete (oblate) Ellipsoid bei Rotation um die kleine Halbachse b.
Ein Beispiel für ein verlängertes Rotationsellipsoid ist die Form des Rugbyballs, das abgeplattete ähnelt einer Schokolinse.
Inhaltsverzeichnis
Vorkommen
Die meisten größeren Himmelskörper sind angenähert abgeplattete Rotationsellipsoide (auch Sphäroide genannt). Sie entstehen durch die Fliehkraft, die bewirkt, dass ein sich drehender kugelförmiger Körper verformt wird. An den Polen, also den Durchstoßpunkten der Rotationsachse, werden diese Körper abgeplattet, am Äquator entsteht eine Ausbauchung. Besonders deutlich ist die Abplattung bei den großen Gasplaneten Jupiter und Saturn ausgeprägt, weil sie besonders schnell rotieren und nicht verfestigt sind. Aber auch die Erde und die anderen terrestrischen Planeten werden durch die bei der Rotation entstehenden Fliehkräfte zu Rotationsellipsoiden verformt. Der in zehn Stunden rotierende Jupiter ist um etwa 1/16 abgeplattet, die Erdabplattung beträgt 1/298,257223563 (WGS 84). Elliptische Galaxien sind oft keine Rotationsellipsoide, sondern triaxial.
Volumen
Das Volumen des verlängerten Rotationsellipsoids beträgt
und das des abgeplatteten
Oberfläche
Die Oberfläche für das verlängerte Ellipsoid berechnet man mit
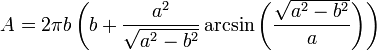 ,
,
die des abgeplatteten mit
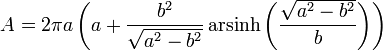 .
.
Anwendung
In der Geodäsie, Kartografie und den anderen Geowissenschaften werden Rotationsellipsoide als geometrische Annäherung an das (physikalische) Geoid benutzt. Diese Rotationsellipsoide dienen dann als Referenzfläche, um die Lage bzw. Höhe von Objekten der Erdoberfläche anzugeben. Man spricht dann von einem Referenzellipsoid.
In einem Hohlkörper reflektieren die Begrenzungsflächen des Rotationsellipsoiden die Strahlung von einem Brennpunkt zum anderen. Den Effekt nutzt ein Flüstergewölbe für die Bündelung von Schallwellen.
Berechnung der Oberflächenformeln
Sei
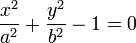 die Gleichung der Ellipse mit den Halbachsen a und b (a > b).
die Gleichung der Ellipse mit den Halbachsen a und b (a > b).Verlängertes Rotationsellipsoid
Mit der ersten guldinschen Regel
![A = 2\pi\int_{-a}^a f(x)\sqrt{1+\left[f'(x)\right]^2}\mathrm{d}x](/pictures/dewiki/56/89d6a8dd26fd37b2e557a66fe5468da8.png) lässt sich die Oberfläche des Rotationskörpers berechnen, der durch die um die x-Achse rotierende Ellipse erzeugt wird. Dabei nimmt man
lässt sich die Oberfläche des Rotationskörpers berechnen, der durch die um die x-Achse rotierende Ellipse erzeugt wird. Dabei nimmt man 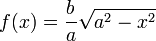 als erzeugende Linie, die sich aus der Ellipsengleichung durch Auflösen nach y ergibt.
als erzeugende Linie, die sich aus der Ellipsengleichung durch Auflösen nach y ergibt.Außerdem wird noch ein Integral benötigt, das sich über die Ableitung der rechten Seite nach x verifizieren lässt:
Einsetzen von f und f' in die guldinsche Regel liefert
Im letzten Ausdruck wurde die Spiegelsymmetrie des Integranden um x = 0 ausgenutzt. Nun braucht man nur noch das pq-Integral mit der Obergrenze x = a (die Untergrenze trägt nicht bei) und die Parameter q = a4 und p = a2 − b2 einzusetzen und erhält
was nach dem Vereinfachen die gewünschte Formel darstellt.
Abgeplattetes Rotationsellipsoid
Diese Rechnung verläuft ähnlich der vorigen, man lässt die Ellipse jetzt aber um die y-Achse rotieren. [xl,xr] ist das Intervall der betrachteten Profillinie (hier [0,a]). Mit der ersten guldinschen Regel in der Form
und der Umkehrfunktion
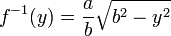 (Auflösen der Ellipsengleichung nach x) und einsetzen von f(0) = b sowie f(a) = 0 findet man
(Auflösen der Ellipsengleichung nach x) und einsetzen von f(0) = b sowie f(a) = 0 findet manHier wurde wiederum die Symmetrie der Ellipse ausgenutzt und außerdem die Integrationsgrenzen so angeordnet, dass sich ein positives Resultat ergibt.
Substituiert man im pq-Integral x = iy, so ergibt sich die an dieser Stelle passende verwandte Form
Einsetzen des Integrals mit der Obergrenze y = b und der Parameter q = b4 und p = a2 − b2 resultiert in
Vereinfachen liefert den oben zitierten Ausdruck für die Oberfläche des abgeplatteten Rotationsellipsoids. Das Ergebnis lässt sich auch unter Verwendung der numerischen Exzentrizität
darstellen und mit der Ersetzung
in eine häufig verwendete Form bringen.
Beide Oberflächenformeln gehen bei Vertauschen von a und b (entspricht einer Drehung der das Rotationsellipsoid erzeugenden Ellipse um 90 Grad) ineinander über.
Wikimedia Foundation.

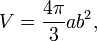
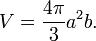
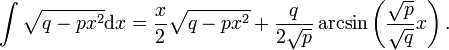
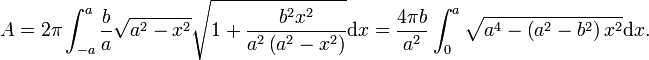
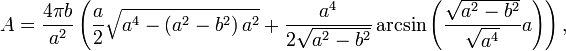
![A = 2\pi\int_{\min(f(x_l),f(x_r))}^{\max(f(x_l),f(x_r))} f^{-1}(y)\sqrt{1+\left[\left(f^{-1}(y)\right)'\right]^2}\mathrm{d}y](/pictures/dewiki/54/635fe7df625f0fd028e04f531ce18073.png)