Geoid

Erdschwerefeld: Lotlinie durch P, Geoid (V = Vo und Äquipotentialflächen Vi)

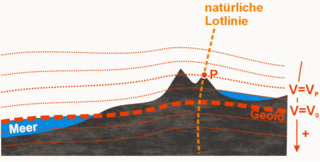
Das Geoid ist eine Bezugsfläche im Schwerefeld der Erde zur Vermessung und Beschreibung der Erdfigur. In guter Näherung wird das Geoid durch den mittleren Meeresspiegel der Weltmeere repräsentiert und ist damit in seiner Form außerhalb der Landmassen sichtbar. Das Potential der Erdschwere ist an jedem Ort der Geoidfläche gleich. Die natürliche Lotrichtung und das Geoid stehen in jedem Punkt senkrecht zueinander. Daher kann das Geoid durch Messung der Schwerkraft bestimmt werden. Zwei beliebige Punkte auf dem Geoid haben das gleiche Schwerepotential und deshalb die gleiche dynamische Höhe. Die Schwerebeschleunigung g ist hingegen auf dem Geoid nicht konstant, sondern sinkt vom Pol zum Äquator von 9,83 auf 9,78 m/s². ^{[Voellmy, S.159]}

Das Geoid ist ein physikalisches Modell der Erdfigur, das 1828 von Gauß entwickelt wurde – im Gegensatz zum geometrischen Modell des Erdellipsoids. Die Bezeichnung „Geoid“ geht auf Johann Benedict Listing zurück, der es 1871 als Fläche gleichen Schwerepotentials beschrieb.

Geoid-Konstruktion

Von den unendlich vielen, ähnlich Zwiebelschalen um den Erdmittelpunkt geschachtelten Flächen mit konstantem Schwerepotential (Äquipotentialflächen) wurde diejenige als Geoid ausgewählt, welche dem mittleren Meeresspiegel bestmöglich entspricht. Denn der mittlere Meeresspiegel kann durch Pegelbeobachtung erdumspannend als Bezugsfläche für Höhenmessungen und Schweremessungen bestimmt werden. Die europäischen Länder haben Pegel an verschiedenen Küstenorten wie beispielsweise in Amsterdam und Triest für die Bestimmung des Geoids als Höhenbezugsfläche (siehe Höhe über dem Meeresspiegel) vermessen.

Die Bestimmung der Geoidfläche erfolgte anfangs durch astronomische Bestimmung der Lotrichtung und durch einzelne örtlichen Schweremessungen mit dem Gravimeter. Die Höhenvermessung der Meeresoberfläche durch Satellitenaltimetrie und die Verdichtung der Schweremessung durch die Landesvermessungen in der zweiten Hälfte des 20. Jahrhunderts verbesserten die Genauigkeit der Geoidbestimmung wesentlich. Heute dominieren die Verfahren der Satellitengeodäsie die Bestimmung des Erdschwerefeldes.

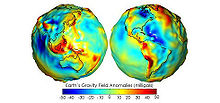
Die genauen Messungen der Satelliten zeigen das Geoid als eine unregelmäßige Fläche mit vielen Beulen und Dellen. Diese werden durch Schwereanomalien und ungleichmäßige Verteilung der Erdmassen verursacht. Wegen seiner unregelmäßigen Form ist das Geoid mathematisch sehr schwer zu beschreiben. Die praktische Landesvermessung und Kartografie benötigt aber eine mathematisch einfach definierte Erdfigur als Bezugsfläche für Berechnungen und Kartenabbildungen. Solche Bezugsflächen sind meist Rotationsellipsoide, welche das Geoid gut approximieren. Diese mathematisch definierten Flächen können aber nicht direkt durch Messen physikalischer Größen bestimmt werden.

Deshalb muss für die praktische Handhabung die Abweichung zwischen der physikalischen und messtechnisch erfassbaren Beschreibung (Geoid) sowie der mathematischen und für Berechnungen geeigneten Beschreibung (Rotationsellipsoid) der Erdfigur bestimmt werden.

Die Abweichungen des Geoids von einem Referenzellipsoid (ED50, WGS84, GRS 80) werden als Geoidundulation bzw. Geoidhöhe bezeichnet und können regional bis 100 m ausmachen.

Geoidundulation N = h − H, mit ellipsoidischer (geometrischer) Höhe h und orthometrischer (physikalischer) Höhe H

Geoid-Näherungen

Erdschwerefeld, Abweichungen stark überhöht

In nullter Näherung ist das Geoid unter Vernachlässigung des Potentials der Zentrifugalkraft U_z eine Äquipotentialfläche im Gravitationsfeld eines Massepunktes: U(r) = G·M/r + U_z (G: Gravitationskonstante, M: Masse der Erde, r: Abstand vom Mittelpunkt der Erde). Für viele Rechnungen der Himmelsmechanik liefert diese Vereinfachung brauchbare Ergebnisse. Das Geoid ist eine Kugel mit einem Parameter R≈6373 km für den Radius.

Abweichungen von der Kugelform lassen sich durch Legendre-Polynome P_n(cos(θ)) beschreiben (θ: Breitenwinkel, R: mittlerer Erdradius, J_n: Entwicklungskoeffizienten):

$U(r, \theta) = \frac{G M}{r} \sum_{n = 0, 1, \dots} \left(\left(\frac{R}{r}\right)^n J_n \cdot P_n \left(\cos(\theta)\right)\right) + U_\mathrm{z}$

mit den Koeffizienten:

J₀ = 1; Kugelnäherung

J₁ = 0; kein Dipolmoment, Nord- und Südhalbkugel gleich schwer

J₂ = 1082,6·10^-6; Näherung als Rotationsellipsoid mit gleichgroßen Halbachsen a=b≈6378 km in der Äquatorebene und c≈6357 km in Polrichtung.

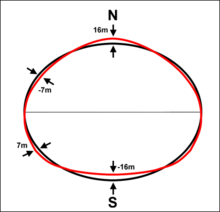
J₃ = 2,51·10^-6; Näherung einer birnenähnlichen Struktur (siehe Zeichnung)

J₄ = 1,60·10^-6

Birnenform als Näherung der Erdfigur im Vergleich zum elliptischen Querschnitt (schwarze Linie).

Veranschaulichung der Schwerevariation entlang des Äquators, bezogen auf eine kreisförmige Referenzfläche (schwarz).

Die geometrischen Abweichungen von einer Ellipse betragen weniger als 20 m. Die starke Überhöhung in der Zeichnung links veranschaulicht, warum die Erde manchesmal als birnenförmig beschrieben wird.

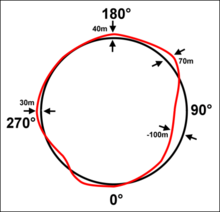
Eine verbesserte Näherung führt weitere Koeffizienten ein, die die Abhängigkeit von der geographischen Länge berücksichtigen. Die Schemazeichnung rechts macht deutlich, dass Schwereabweichungen im Längengrad vorliegen, die einem Höhenunterschied von fast 150 m entsprechen. Sie sind die Ursache dafür, dass es für geostationäre Satelliten nur zwei stabile und zwei labile Bahnpositionen gibt.

Geoidbestimmung

→ Hauptartikel: Geoidbestimmung

Die derzeit genaueste Geoidbestimmung erfolgt durch die Satelliten CHAMP und GRACE. Bei solcher Geoidbestimmung mit Satelliten analysiert man jene Bahnstörungen, die durch die Unregelmäßigkeit der Erdfigur und der Massenverteilungen im Erdinnern auf Umlaufbahnen wirken. Man kann aber auch vom Satellit mittels Altimetrie die Form der Meeresoberfläche direkt messen. Hierbei stellte man allerdings fest, dass die mittlere Meeresoberfläche (also Gezeiten und Wellen herausgemittelt) um bis zu etwa 1 Meter von der Geoidfläche abweicht. Die Meeresoberfläche stellt also genaugenommen nicht exakt eine Niveaufläche dar, sondern weicht aufgrund großräumiger Meeresströmungen minimal davon ab.

Die Geoidbestimmung kann außerdem mit Methoden der Astrogeodäsie oder gravimetrisch erfolgen. Die Methode der Bestimmung des Astro-Geoids (Messung der Lotabweichung) wurde schon vor 100 Jahren erprobt und war lange Zeit die genaueste, erfordert aber festen Boden. Ein wichtiges Instrument der Astrogeodäsie ist die Zenitkamera: mit ihrer Hilfe kann durch Aufnahme des zenitalen Sternfeldes die Lotrichtung in einem Messpunkt mit einer sehr hohen Genauigkeit bestimmt werden. Diese Lotrichtungen beziehen sich auf das Schwerefeld und damit auf das Geoid. Um Lotabweichungen als Maß der Neigung des Geoids gegenüber dem Referenzellipsoid zu bestimmen, ist die Kenntnis der ellipsoidischen Koordinaten des Messpunktes erforderlich. Diese können mittels GNSS (Globales Navigationssatellitensystem) bestimmt werden.

Bei der Gravimetrie wird das Geoid über die Messung der Schwere bestimmt. In der Landesvermessung hatte die Gravimetrie vor allem in der zweiten Hälfte des 20. Jahrhunderts großen Anteil an der Bestimmung des Schwerefeldes. Für eine globale Geoidbestimmung durch hinreichend dichte Verteilung der Messpunkte ist das Verfahren allerdings zu aufwändig.

Im Juni 2011 veröffentlichte das GFZ das Schweremodell "EIGEN-6C".^[1][2] Dieses globale Modell wurde aus den kombinierten Daten verschiedener Sat-Messungen von LAGEOS, GRACE, GOCE und anderen Messmethoden erstellt und hat eine räumliche Auflösung von ca. 12km.

Ursachen der Geoidundulationen

Dichteanomalien im Erdmantel aufgrund von Mantelkonvektion und mit ihnen verbundenen Topografievariationen sind die Ursache für den Hauptteil der beobachteten Geoidundulationen.

Die Ursachen für die langwelligen Geoidschwankungen (Geoidundulationen) liegen in großräumigen Dichtevariationen im Erdmantel und zu geringerem Maße auch in der Erdkruste. Eine anomal höhere Gesteinsdichte erzeugt eine zusätzliche Gravitationsbeschleunigung und beult somit das Geoid aus, geringere Dichten führen zu „Dellen“ im Geoid. Aber auch die Topografie selbst stellt eine lateral variable Massenvariationen dar (siehe Hebung) und führt zu Geoidundulationen. Die Ursache für Dichtevariationen im Erdmantel liegt in der Mantelkonvektion: heiße Mantelregionen sind weniger dicht und steigen auf (mantle plumes), kalte, dichte Regionen sinken ab. Man würde nun also über aufsteigenden Konvektionsströmen „Dellen“ im Geoid erwarten, über abtauchenden Konvektionsströmen (beispielsweise über Subduktionszonen) „Beulen“. Dies stimmt im Großen und Ganzen für den West-Pazifik mit den Beobachtungen überein. Die Sache wird aber dadurch komplizierter, dass aufsteigende Konvektionsströme die Erdoberfläche selbst auch anheben (Beispiel Island, Hawaii). Die dadurch erzeugte Topografie bezeichnet man als dynamische Topografie. Hierdurch wird die eigentliche negative Geoidundulation abgeschwächt und kann sogar positiv werden. Ein Beispiel hierfür scheint Island zu sein. Der Effekt der dynamischen Topographie hängt auch noch von der Viskosität des Erdmantels ab und ist schwierig zu quantifizieren. Heute benutzt man Information aus der Seismologie, um Dichten im Mantel abzuschätzen und das Geoid und die dynamische Topographie zu berechnen und kann dann aus Vergleich mit dem beobachteten Geoid Rückschlüsse auf die Mantelviskosität ziehen.

Siehe auch

• Quasigeoid
• orthometrische Höhe
• Schwereanomalie

Literatur

• Christoph Reigber, Peter Schwintzer: Das Schwerefeld der Erde. Physik in unserer Zeit 34(5), S. 206–212 (2003), ISSN 0031-9252.
• Erwin Groten: Geodesy and the Earth’s Gravity Field – Vol.I Principles and Conventional methods. Bonn 1979.
• Intergovernmental Committee On Surveying & Mapping: Geocentric Datum of Australia – Technical Manual, Version 2.2. PDF, Stand: 2005.
• Wolfgang Torge: Geodäsie. 2. Auflage. Walter de Gruyter, Berlin u.a. 2003, ISBN 3-11-017545-2
• Zenner, Lieselotte: Analyse und Vergleich verschiedener Schwerefeldlösungen. zfv Zeitschrift für Geodäsie, Geoinformation und Landmanagement, Heft 3/2007 - 132. Jahrgang, Wißner-Verlag, Augsburg 2007
• Voellmy, Erwin: Mathematische Tafeln und Formeln. 17. Auflage. Orell Füssli, Zürich 1973, ISBN 3-280-00682-1

Weblinks

• Klaus Pionzik: Die Gestalt der Erde (mit Vorbehalt; populäre Darstellung)
• Norbert Kühtreiber: High Precision Geoid Determination of Austria Using Heterogeneous Data (Theorie)
• LVA NRW: Normalhöhen in Nordrhein-Westfalen
• Stefan A. Voser: Geometrische Anforderungen beim Datenaustausch
• EUREF: Links zu Geoid-Informationen
• Umrechnung zwischen WGS84 Referenz-Ellipsoid und EGM96 Geoid

Einzelnachweise

1. ↑ Die jahreszeitliche Kartoffel gfz-potsdam.de, abgerufen am 30. Juni 2011
2. ↑ Jahreszeitliche Schwankungen der planetaren "Kartoffel" messbar derstandard.at