- Stern (Geometrie)
-
In der Geometrie versteht man unter einem Stern ein reguläres (gleichseitiges und gleichwinkliges) überschlagenes (nicht-konvexes) ebenes Polygon. Überschlagen bedeutet, dass sich die Seiten innerhalb des Polygons schneiden.
Hiervon zu unterscheiden sind die in der Topologie und Analysis betrachteten Sterngebiete, zu denen auch die konvexen Mengen gehören und die nicht polygonal zu sein brauchen.
Inhaltsverzeichnis
Konstruktion
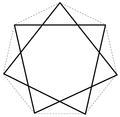
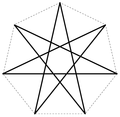
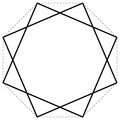
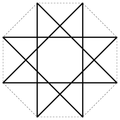
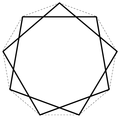
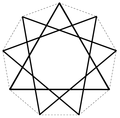
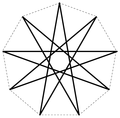
Ein Stern entsteht, indem man in einem ebenen regelmäßigen p-Eck, ausgehend von jedem Eckpunkt, diesen mit einem nicht benachbarten Eckpunkt verbindet und dieses Verfahren fortsetzt, bis der ursprüngliche Eckpunkt wieder erreicht wird. Das Verfahren kann auch als das Verbinden jeden q-ten Punktes eines gleichmäßigen mit p Punkte unterteilten Kreisumfangs beschrieben werden. Ein p-Eck kann in Abhängigkeit von p mehr als eine Sternkonstruktion erzeugen. Die Schreibweise für einen solchen Stern ist {p/q} (Schläfli-Symbol). Hierbei gilt, sind p und q teilerfremd, lässt sich der Stern in einem Zug zeichnen.
Ecken Anzahl Schläfli-Symbol Bezeichnung Spitzenwinkel (teils gerundet)
q=2,3,...3 0 4 0 5 1 {5/2} Pentagramm 36° 6 1 {6/2} Hexagramm 60° 7 2 {7/2}, {7/3} Heptagramm ~77°, ~26° 8 2 {8/2}, {8/3} Oktagramm, Achtort 90°, 45° 9 3 {9/2}, {9/3}, {9/4} Enneagramm 100°, 60°, 20° 10 3 {10/2}, {10/3}, {10/4} Dekagramm 108°, 72°, 36° 11 4 {11/2}, {11/3}, {11/4}, {11/5} Hendekagramm ~115°, ~82°, ~49°, ~16° 12 4 {12/2}, {12/3}, {12/4}, {12/5} Dodekagramm 120°, 90°, 60°, 30° 13 5 {13/2}, {13/3}, {13/4}, {13/5}, {13/6} Tridekagramm ~125°, ~97°, ~69°, ~42°, ~14° ... ... ... ... ... 20 8 {20,2}, {20/3}, {20/4}, {20/5}, {20/6}, {20/7}, {20/8}, {20/9} Icosagramm 144°, 126°, 108°, 90°, 72°, 54°, 36°, 18° p 

Anmerkung: Die nur unten mit einem Haken versehenen Klammern (Gauß-Klammer) stehen für das Abrunden.
Abbildungen
-
Pentagram.svg
{5/2}-Stern
-
{8/2}-Stern (Achtort)
-
{8/3}-Stern Achterstern
Siehe auch
Sternpolyeder
Weblinks
-
Wikimedia Foundation.