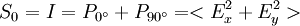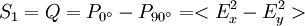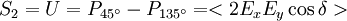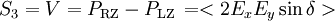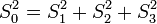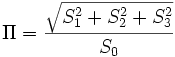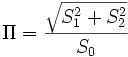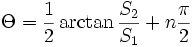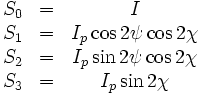Stokes-Vektor

Die Stokes-Parameter sind ein Satz von vier Werten, meist als S₀…S₃ oder I, Q, U und V bezeichnet, die 1852 von George Gabriel Stokes zur Beschreibung des Polarisationszustandes elektromagnetischer Wellen (meist Licht) eingeführt wurden. Das Besondere an diesen Werten ist, dass sie durch einfache Messungen der Lichtleistung nach Durchgang durch verschiedene Polarisatoren berechnet werden können und so der Polarisationszustand recht einfach bestimmt werden kann.

Die vier Stokes-Parameter S₀…S₃ können zum sog. Stokes-Vektor zusammengefasst werden.

Definition

$S_0 = I = P_{0^\circ}+P_{90^\circ}= <E_x^2+E_y^2>$

$S_1 = Q = P_{0^\circ}-P_{90^\circ}=<E_x^2-E_y^2>$

$S_2 = U = P_{45^\circ}-P_{135^\circ}=<2E_x E_y \cos\delta>$

$S_3 = V =P_{\rm RZ} - P_{\rm LZ}\,=<2E_x E_y \sin\delta>$

Die Leistungen sind dabei die gemessene Leistung nach Durchgang durch einen horizontal (0°), vertikal (90°), 45° und 135° orientierten, idealen Polarisator sowie der rechts- und links-zirkular polarisierte Anteil des Lichts.

Alternativ lassen sie sich über die zeitgemittelten Amplituden E_x , E_y der elektrischen Wellenvektoren in einem orthogonalen Koordinatensystem, sowie deren relativer Phase δ definieren.

Üblicherweise werden die Stokes-Parameter auf die einfallende Leistung normiert, indem alle vier Werte durch S₀ dividiert werden.

Für vollständig polarisiertes Licht gilt:

$S_0^2=S_1^2+S_2^2+S_3^2$

Für unpolarisiertes Licht hingegen gilt S₁ = S₂ = S₃ = 0. Es lässt sich ein Polarisationsgrad Π definieren durch:

$\Pi=\frac{\sqrt{S_1^2+S_2^2+S_3^2}}{S_0}$

Beziehungsweise für nur linear polarisiertes Licht:

$\Pi=\frac{\sqrt{S_1^2+S_2^2}}{S_0}$

Der Winkel der maximalen Polarisation ist definiert durch:

$\Theta=\frac{1}{2} \arctan{\frac{S_2}{S_1}}+n \frac{\pi}{2}$

wobei n = 1 für S₁ < 0, ansonsten ist n = 0. Anders ausgedrückt bedeutet das, dass man 90° zum Winkel Θ hinzu zählen muss, wenn S₁ kleiner als 0 ist.

Eine andere Formulierung findet sich in Kugelkoordinaten:

$\begin{matrix} S_0 &amp;amp;=&amp;amp; I \\ S_1 &amp;amp;=&amp;amp; I_p \cos 2\psi \cos 2\chi\\ S_2 &amp;amp;=&amp;amp; I_p \sin 2\psi \cos 2\chi\\ S_3 &amp;amp;=&amp;amp; I_p \sin 2\chi \end{matrix}$

Wobei I die Gesamtintensität, I_p der polarisierte Anteil der Intensität, ψ die Verkippung der Polarisationsellipse und tanχ das Verhältnis der beiden Hauptachsen der Polarisationsellipse ist.

Beispiele

Polarisation	Stokes-Vektor	Polarisation	Stokes-Vektor
linear, horizontal	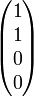$\begin{pmatrix} 1\\ 1\\ 0\\ 0 \end{pmatrix}$	links-zirkular	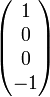$\begin{pmatrix} 1\\ 0\\ 0\\ -1 \end{pmatrix}$
linear, vertikal	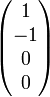$\begin{pmatrix} 1\\ -1\\ 0\\ 0 \end{pmatrix}$	rechts-zirkular	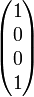$\begin{pmatrix} 1\\ 0\\ 0\\ 1 \end{pmatrix}$
linear, +45°	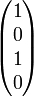$\begin{pmatrix} 1\\ 0\\ 1\\ 0 \end{pmatrix}$	unpolarisiert	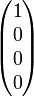$\begin{pmatrix} 1\\ 0\\ 0\\ 0 \end{pmatrix}$

Die Wirkung optischer Systeme auf Stokes-Vektoren wird im Mueller-Kalkül durch Anwendung entsprechender Matrizen behandelt.

Weblinks

http://www.astro.uni-jena.de/Teaching/Praktikum/pra2002/node235.html

Literatur

• William A. Shurcliff: Polarized Light: Production and Use. Harvard University Press, Cambridge, Mass. 1962, ISBN 0674682505. 
• Craig F. Bohren, Donald R. Huffman: Absorption and scattering of light by small particles. Wiley, New York 1998, ISBN 0-471-29340-7.