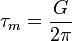Superversetzung

Schematische Darstellung einer Stufenversetzung und ihres Burgersvektors.

TEM-Aufnahme von Versetzungen in einer Legierung.

Darstellung einer Stufenversetzung in einem Kristall

In der Werkstoffwissenschaft ist eine Versetzung ein modellhaftes Objekt, das einen eindimensionalen Gitterfehler in einem Kristall darstellt. Sie entsteht beim Kristallwachstum aus der Schmelze oder bei der Rekristallisation im festen Zustand, infolge von Eigenspannungen oder bei der plastischen Verformung und wird durch eine Versetzungslinie dargestellt. Plastische Verformung von Kristallen geschieht meistens über die Erzeugung und Bewegung von Versetzungen. Eine Versetzung kann in der Mitte eines Kristalls nicht aufhören.

Eigenschaften und Typen

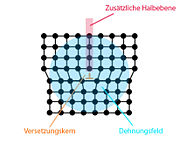
Man kann sich eine Versetzung als eine zusätzliche Halbebene von Teilchen (Atome, Ionen) vorstellen, die in einen perfekten Kristall eingeschoben ist. Den Ort, wo diese Halbebene endet, nennt man den Versetzungskern oder die Versetzungslinie. Dort bewirkt die Versetzung die stärkste Verzerrung des Gitters, was ein hochenergetisches Dehnungsfeld um die Versetzungslinie herum ergibt.

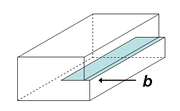
Jede Versetzung hat zwei wichtige Parameter: den Burgersvektor 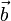$\vec{b}$ (benannt nach W. G. Burgers) und die Versetzungslinie. Es gibt zwei Grundtypen von Versetzungen:

• Stufenversetzungen und
• Schraubenversetzungen.

Wenn der Burgersvektor und die Versetzungslinie senkrecht zueinander stehen, so spricht man von einer Stufenversetzung; liegen sie parallel, so handelt es sich um eine Schraubenversetzung. Es gibt jedoch auch beliebige Mischformen zwischen diesen beiden Grundtypen, wenn der Burgersvektor und die Versetzungslinie weder parallel noch senkrecht sind.

Der Burgersvektor hat eine Richtung und einen Betrag, und beschreibt die Richtung, in der die Bewegung unbedingt vorkommt. Der Betrag entspricht immer der Entfernung zwischen zwei benachbarten Atomen in dieser Richtung, und die Richtung wird von der Kristallstruktur diktiert. Der Burgersvektor mit der niedrigsten Energie (wächst mit dem Quadrat seines Betrages) liegt in dichtgepackten Ebenen: in einem kubisch flächenzentrierten Gitter ist es in der <110> Richtung; in einem kubisch raumzentrierten Gitter ist es in der <111> Richtung. Die Energie einer Versetzung beträgt E = 1 / 2Gb² (G = Schubmodul). Daraus lässt sich ableiten, dass die Energie eines Kristalls absinkt, wenn sich die Versetzung in zwei Partialversetzungen mit jeweils nur halb so großem Burgersvektor aufspaltet.

Der Burgersvektor

Ermittlung des Burgersvektors

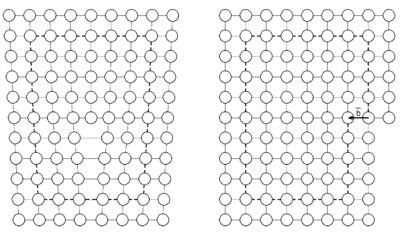
Der Burgersvektor lässt sich mit folgendem Gedankenspiel bilden:

• Mit etwas Abstand zur Versetzung wird eine Verbindung zwischen den Atomen gezogen, sodass ein geschlossener Umlauf entsteht.
• Dies ist der Burgers-Umlauf, dargestellt durch die gestrichelte Linie.
• Nun wird der Umlauf auf das ungestörte Gitter übertragen.
• Anfangs- und Endpunkt des Umlaufs sind verschieden.
• Die Verbindung, die nötig ist, um den Umlauf zu schließen, ist der Burgersvektor $\vec{b}$.

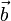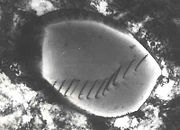
Sichtbarmachung von Versetzungen

Obwohl es sich bei dem Versetzungskonzept „nur“ um ein physikalisches Modell handelt, sind die Gitterverzerrungen um eine Versetzungslinie real und können mit einer Reihe von Methoden sichtbar gemacht werden. Diese eignen sich grundsätzlich auch zur Bestimmung der Versetzungsdichte ρ (siehe dort).

• Ätzen
• IR-Mikroskopie
• Transmissionselektronenmikroskopie (TEM)
• Feldionenmikroskopie (FIM)

Versetzungsbewegung und Plastizität

Bis in die 1930er Jahre war es eine große Herausforderung, die Plastizität und Festigkeit der Metalle auf mikroskopischer Ebene zu erklären. In einem „defektfreien“ Kristall wird die theoretische Festigkeit τ_m durch den Ausdruck

$\tau_m = \frac {G} {2 \pi}$

beschrieben (G = Schubmodul). Doch die tatsächlich beobachteten Werte liegen für praktisch alle Metalle ein Vielfaches unter dieser Abschätzung.

1934 entdeckten Egon Orowan, Michael Polanyi und G. I. Taylor unabhängig und etwa gleichzeitig, dass dieser Widerspruch durch das Versetzungskonzept aufgelöst werden kann.

Unter der Wirkung einer im Vergleich zur theoretischen Festigkeit sehr kleinen Schubspannung können sich Versetzungen „bewegen“, d. h. die Atome der benachbarten Halbebene brechen ihre Bindungen kurzzeitig auf und binden sich an die der nächsten Halbebene an. Die Versetzungslinie „wandert“ scheinbar. Dies ist der elementare Mechanismus der plastischen Verformung. Er geschieht immer nur in solchen sogenannten Gleitebenen, in denen auch der Burgersvektor liegt. Außer bei reinen Schraubenversetzungen, die auch quergleiten können, ist die Gleitebene durch die Lage der Versetzung im Gitter bereits fest vorgegeben. Der Verlauf der Versetzungslinie kann jedoch auch durch die Wechselwirkung mit Leerstellen, z. B. beim Klettern, oder anderen Versetzungen gestört werden. Diese Prozesse führen zu einer Behinderung des Gleitprozesses und damit zu einer zunehmenden Kaltverfestigung des Kristalls und zur Bildung neuer Versetzungen (sog. Versetzungsmultiplikation).

Die Kaltverfestigung ist irreversibel, solange die Temperatur unterhalb ca. 30 % der absoluten Schmelztemperatur T_m (in [K]) bleibt. Darüber kann es zur Ausheilung (Kristallerholung) der Versetzungen durch Rekombination oder Anordnung der Versetzungen zueinander kommen, wodurch die Festigkeit wieder deutlich sinkt und die Verformbarkeit steigt. Bei noch höheren Temperaturen werden die Versetzungen durch Gefügeneubildung beim Rekristallisationsglühen beseitigt.

Versetzungen in Halbleitern

In der Halbleiterindustrie werden möglichst versetzungsarme Einkristalle benötigt, da sonst die elektronischen Eigenschaften der Kristalle nachhaltig gestört würden. Großtechnisch können heute bei Silizium und Germanium mit (<< 10⁸ 1/cm²) die niedrigsten Versetzungsdichten erreicht werden, während sie bei allen anderen Kristallen in makroskopisch relevanten Volumina immer um Größenordnungen höher liegt. Weiter liegt die Dichte für die technologisch bedeutenden Halbleiter GaAs bei ca. (10⁸ 1/cm²) bzw. für die mittels Heteroepitaxie gewachsenen GaN-Schichten bei (10¹⁰ 1/cm²) . Die Versetzungen kommen vor allem durch thermische Spannungen beim Abkühlprozess in das Material. Möglichst versetzungsarme Kristalle erhält man daher bei schonender Abkühlung.

Siehe auch

• Versetzungsdichte
• Zwillingsbildung

Literatur

• D. Hull, D. J. Bacon: Introduction to Dislocations. Pergamon Press, Oxford 1984, ISBN 0-08-028720-4.

• H. Kleinert, Gauge Fields in Condensed Matter, Vol. II, "STRESSES AND DEFECTS; Differential Geometry, Crystal Melting", pp. 743-1456, World Scientific (Singapur, 1989); Paperback ISBN 9971-50-210-0 (auch online lesbar hier)

Weblinks

• Physikalische Werkstoffeigenschaften (Ausführliches Vorlesungsskript TU Dresden)