Sylowsätze

Die Sylow-Sätze sind drei mathematische Sätze aus der Algebra. Die nach dem Norweger Peter Sylow benannten Sätze erlauben es, Aussagen über Untergruppen von endlichen Gruppen zu treffen und auch einige Gruppen endlicher Ordnung zu klassifizieren. Dies ist mit diesen Mitteln aber nur in sehr beschränktem Maße möglich, eine vollständige Klassifikation endlicher Gruppen vollzieht sich über die Klassifikation der einfachen endlichen Gruppen und der Beweis dazu umfasst 15.000 Seiten.

Die Sätze

Sei im folgenden G eine endliche Gruppe der Ordnung | G | = p^rm, wobei p eine Primzahl und m eine zu p teilerfremde natürliche Zahl sei.

1. Für die Anzahl s_p der Untergruppen der Ordnung p^r gilt:

$s_p \equiv 1 \mod p$

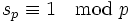
(d.h. s_p lässt bei Division durch p den Rest 1) und 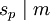$s_p \mid m$. Insbesondere ist s_p niemals null. Diese Untergruppen sind die maximalen p-Untergruppen von G, diese nennt man auch die p-Sylow-Untergruppen von G.

2. Es sei H eine Untergruppe der Ordnung p^s, mit s < r. Dann ist H in einer p-Sylow-Untergruppe von G enthalten.

3. Alle p-Sylow-Untergruppen sind zueinander konjugiert.

Wenn es zu einem p nur eine Sylow-Untergruppe gibt, muss sie ein Normalteiler von G sein. Diesen Sachverhalt kann man zum Beispiel benutzen, um zu zeigen, dass es keine einfache Gruppe einer bestimmten endlichen Ordnung gibt.

Beispiele

Jede Gruppe der Ordnung 15 ist zyklisch

Sei G eine Gruppe der Ordnung 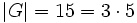$|G|=15=3 \cdot 5$, dann gilt:

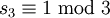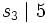1. $s_3 \equiv 1 \;\operatorname{mod}\; 3$ und $s_3 \mid 5$, also muss s₃ = 1 gelten.
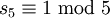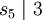2. $s_5 \equiv 1 \;\operatorname{mod}\; 5$ und $s_5 \mid 3$, also muss s₅ = 1 gelten.

Also sind die 3-Sylow-Gruppe G₃ und die 5-Sylow-Untergruppe G₅ Normalteiler von G. Als p-Untergruppen zu verschiedenen Primzahlen schneiden sie sich in 1, daher ist ihr Komplexprodukt direkt 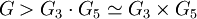$G&amp;gt;G_3\cdot G_5\simeq G_3\times G_5$ (s. Komplementäre Normalteiler und direktes Produkt). Da das direkte Produkt die Ordnung 15 hat, folgt $G \simeq \mathbb{Z}/3\mathbb{Z} \times \mathbb{Z}/5\mathbb{Z} \simeq \mathbb{Z}/15\mathbb{Z}$.

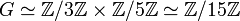Es gibt keine einfache Gruppe der Ordnung 162

Sei $|G| = 162= 2\cdot 3^4$

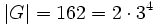
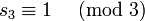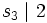Aus $s_3 \equiv 1 \; \pmod{3}$ und $s_3 \mid 2$ folgt s₃ = 1

Also ist die 3-Sylow-Gruppe ein Normalteiler von G der Ordnung 3⁴ = 81. Dieser Normalteiler kann somit weder die ganze Gruppe G sein, noch kann er nur aus dem neutralen Element bestehen. G ist also nicht einfach.

Weblinks