Balbus-Hawley-Instabilität

Kleine Magnetfelder sorgen in rotierenden Fluiden unter bestimmten Voraussetzungen dafür, dass die Rotation instabil wird und Materie ins Zentrum fällt. Dieses Phänomen wird als Magnetorotationsinstabilität (MRI, magnetische Rotationsinstabilität) bezeichnet, oder nach seinen Entdeckern auch Balbus-Hawley-Instabilität. Die Instabilität sorgt in astrophysikalischen Akkretionsscheiben u.a. für die Entstehung von Sternen und von Schwarzen Löchern, ist aber auch im Labor beobachtbar. Sie folgt aus den Grundgleichungen der Magnetohydrodynamik (MHD).

Bedeutung

Sowohl bei der Sternentstehung, als auch bei der Entstehung von Schwarzen Löchern sammelt sich Materie in einer Akkretionsscheibe und rotiert um das Zentrum, in dem der Stern entsteht. Die Materie strömt dabei laminar und aufgrund des Dritten Kepler'schen Gesetzes mit nach außen abnehmender Geschwindigkeit. Allerdings besteht dabei kein Grund, warum die Materie nicht auf dieser Bahn beharren, sondern zur Vergrößerung der Sternmasse sich auf das Zentrum zubewegen sollte. Mögliche Ansätze von durch Viskosität erzeugten Turbulenzen erweisen sich nicht als effizient genug, um die Sternentstehung zu verursachen.^[1]

Steven A. Balbus und John F. Hawley zeigten 1991 durch Analyse der Gleichungen der Magnetohydrodynamik, dass kleine Magnetfelder zu Instabilitäten in den rotierenden Scheiben führen. Dies führt dazu, dass Drehimpuls von innen nach außen transportiert wird, und dass die inneren Materieschichten damit ins Zentrum fallen können, so dass sich dort Masse anreichert.^[2]

Phänomen

Die MRI wird durch Scherung des Magnetfeldes im Plasma verursacht. Die Scherung entsteht, da das Magnetfeld dem Plasma folgt und sich die inneren Schichten schneller bewegen als die äußeren (differenzielle Rotation). In einem so gescherten Flächenelement wirkt das Magnetfeld wie eine Feder, die die innere Schicht abbremst, ihr dadurch zugunsten der äußeren Schichten Drehimpuls nimmt und die inner Schicht auf eine niedrigere Umlaufbahn bringt. Dadurch kann Masse in Richtung Gravitationszentrum akkretieren. Die MRI ist also die Ursache für die hohe Akkretionsrate und damit für die hohe Leuchtkraft, die an verschiedenen Objekten (z. B. AGN, Quasare, Mikroquasare) beobachtet wird.

Theorie

Aus der linearen Stabilitätsanalyse der MHD-Gleichungen mit differenzieller Rotation erhält man die Dispersionsrelation:

$\begin{matrix} \left[\omega^2-(\mathbf{k\cdot v_\mathrm{\mathbf{A}}})^2 \right] \cdot \left[\omega^4-k^2\,(c_{\mathrm{s}}^2+v_{\mathrm{A}}^2)\, \omega^2+(\mathbf{k\cdot v_\mathrm{\mathbf{A}}})^2\,k^2c_{\mathrm{s}}^2 \right] & \\ -\left[\kappa^2\omega^4-\omega^2\left(\kappa^2k^2\,(c_{\mathrm{s}}^2+ v_{\mathrm{A\phi}}^2)+(\mathbf{k\cdot v_\mathrm{\mathbf{A}}})^2\dfrac{d\Omega^2}{d(\ln r_\mathrm{zyl})}\right)\right] & \\ -k^2 c_{\mathrm{s}}^2(\mathbf{k\cdot v_\mathrm{\mathbf{A}}}) ^2\dfrac{d\Omega^2}{d(\ln r_\mathrm{zyl})} & =0. \end{matrix}$

ω und k bezeichnen die Frequenz bzw. den Wellenvektor der Störung, 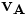$\mathbf{v_A}$ die Alfven-Geschwindigkeit, c_s die Schallgeschwindigkeit, κ die Epizykelfrequenz und Ω die Rotationsfrequenz der Scheibe.

Instabilität tritt ein, wenn ω imaginär wird. Dann erhält man in der Wellengleichung einer Störung 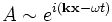$A \sim e^{i(\mathbf{kx} - \omega t)}$ ein exponenzielles Wachstum. Es zeigt sich, dass der langsame Ast der magnetosonischen Welle für genügend schwache Magnetfelder instabil wird, d. h. Störungen wachsen exponenziell. Die charakteristische Wachstumszeit einer Störung ist dabei von der Größenordnung der lokalen Rotationsdauer.

Forschung

Der Effekt wurde bereits 1959 von Evgeny Velikhov und 1960 von Subrahmanyan Chandrasekhar im Zusammenhang mit Stabilitätsbetrachtungen von Couette-Flüssen beschrieben, daher auch die Bezeichnung Velikhov-Chandrasekhar-Instabilität.^[3][4]

Steven A. Balbus^[5] und John F. Hawley^[6] wandten den Effekt auf astrophysikalische Systeme wie differenziell rotierende Akkretionsscheiben an. Sie zeigten die Wirksamkeit der MRI beim Drehimpulstransport theoretisch und in Simulationen. Sie lieferten damit die physikalische Grundlage des 1973 von Nikolai I. Shakura und Rashid Sunyaev entworfenen Modells der Standardscheibe (siehe Akkretionsscheibe).

Heutige Forschung betrachtet z. B. die Wechselwirkung der MRI mit Strahlung, die MRI in resistiven, den Übergang von optisch dichten zu optisch dünnen Scheiben und der Entstehung von Jets aus Akkretionsscheiben.

Siehe auch

• Akkretionsscheibe

Weblinks

• Kapitel in einer Diplomarbeit über Theorie und Simulation der MRI
• Laborexperiment PROMISE im Forschungszentrum Dresden-Rossendorf

Einzelnachweise

1. ↑ J.E. Pringle, ARA&A, 19 (1981) 137.
2. ↑ Steven A. Balbus, John F. Hawley: A Powerful Local Shear Instability in Weakly Magnetized Disks. I - Linear Analysis. II - Nonlinear Evolution. In: The Astrophysical Journal, Part 1. Vol. 376, 20. Juli 1991, ISSN 0004-637X, S. 214–233 (Online ; Stand: 2. Januar 2008). 
3. ↑ E.P. Velikhov, Stability of an Ideally Conducting Liquid Flowing Between Cylinders Rotating in a Magnetic Field, J. Exp. Theoret. Phys., 36:1398–1404 (1959).
4. ↑ S. Chandrasekhar, The stability of non-dissipative Couette flow in hydromagnetics, Proc. Natl. Acad. Sci., 46:253–257 (1960).
5. ↑ Home page of Steven Balbus. Abgerufen am 2. Januar 2008.
6. ↑ John Hawley's Home Page. Abgerufen am 2. Januar 2008.