Taylor-Regel

Die Taylor-Regel ist nach ihrem Erfinder, dem US-Ökonomen John B. Taylor, benannt. Ziel der Regel ist, die Geldpolitik bzw. den von der Zentralbank gesetzten Zinssatz zu bestimmen.^[1]

John B. Taylor

Graphische Darstellung der Taylor-Regel

Taylor versuchte zu ergründen, nach welchen Gesetzmäßigkeiten die US-Zentralbank, das Federal Reserve System (FED), den Zielwert für ihr wichtigstes geldpolitisches Instrument, den kurzfristigen Zinssatz (Federal Funds Rate) auf dem Geldmarkt, festlegt.^[2] Im Gegensatz zur Europäische Zentralbank strebt die amerikanische Zentralbank neben dem Ziel stabiler Preise auch einen hohen Beschäftigungsstand und moderate langfristige Zinsen an. Um die Reaktion der FED auf Änderungsraten der realwirtschaftlichen Entwicklung und der Inflation genau zu quantifizieren und somit einen zielführenden Zinssatz abzuleiten, entwickelte John B. Taylor im Jahr 1993 diese Formel. Sie stellt einen empirischen Ansatz dar, der sich auf ökonomische Untersuchungen stützt. Grundsätzlich beziehen sich die Untersuchungen auf die G8-Staaten und deren Erfolg zur Erreichung ihrer geldpolitischen Ziele. Aus diesem Grund kann die Regel in angepasster Form auf viele andere Länder übertragen werden.^[3] Die Taylor-Regel soll eine Art Handlungsanleitung für Notenbanken sein.^[4]

Taylors Absicht

Ursprünglich war es Taylors Absicht, eine Regel zu ermitteln, die geeignet war, die Zinspolitik der FED (Federal Reserve System) nachzuzeichnen.^[5] Somit hatte er das Ziel, eine Alternative zur Festlegung des kurzfristigen Zinssatzes der Geldpolitik zu entwerfen.^[6] Dabei legte er Wert auf ihre Einfachheit und Robustheit. Sie sollte als Mittel dienen, die Geldpolitik der Zentralbank adäquat zu erfassen und zu bewerten. Aber gleichzeitig sollte sie ein Konzept als Richtschnur für politische Entscheidungen von Zentralbanken sein. Aus einer Gesetzeslage der USA (FED muss Preisniveau- und konjunkturelle Entwicklung berücksichtigen) entstand seine Prämisse, dass die Zentralbanken ihre Zinspolitik in Abhängigkeit von der aktuellen Inflationsrate und der konjunkturellen Situation festlegen.^[7]

Komponenten der Taylor Formel und deren Interpretation

$i^{Tay}=\pi^{erw}+r^*+\alpha \cdot (\pi^{erw}-\pi^{Ziel} )+\beta \cdot ygap$ ^[8]

• erwartete Inflationsrate π^erw
• realer Gleichgewichtszins r*
• „Inflationslücke“ Differenz zwischen erwarteter Inflation π^erw (gemessen am BIP-Deflator) und Inflationsziel π^Ziel (jene, die die Zentralbank mittelfristig anstrebt)
• „Produktionslücke“ bzw. „Output Gap“ (ygap) ist die logarithmische Differenz zwischen dem tatsächlichen realen BIP und dem Produktionspotenzial (definiert als Produktionsvolumen entsprechend der langfristigen Wachstumsrate ^[9]

Die erwartete Inflationsrate (π^erw) und der reale Gleichgewichtszins (r*) liefern in Anlehnung an die Fischergleichung eine Benchmark für den kurzfristigen Zins, dessen Höhe kompatibel mit der Erreichung des Inflationsziels (π = π^Ziel) bei Vollbelastung (y=y*) ist. Die Preisstabilität und das Wirtschaftswachstum bzw. die Konjunkturstabilisierung werden in der Produktions- und Inflationslücke zusammengefasst. Wird das Inflationsziel bei der Inflationslücke überschritten, erfordert dies eine Erhöhung des kurzfristigen Zinses über die Benchmark und umgekehrt. Die Produktionslücke fängt konjunkturelle Aspekte und Preisperspektiven ein. Hier empfiehlt sich eine Senkung des kurzfristigen Zinssatzes bei nicht ausgelasteten Kapazitäten (y<y*) und eine Erhöhung bei voll ausgelasteten Kapazitäten (y>y*). Beide geben an, wie stark die Zentralbank Abweichungen vom Produktionspotenzial und Abweichungen bei der angestrebten Zielinflationsrate geldpolitisch bewertet. ^[10] α und β geben an, wie stark die Geldpolitik auf Veränderungen der Inflationsrate von ihrem Ziel bzw. der Produktion vom Produktionsniveau reagieren sollte. Nach Taylor wird dabei α auf eine Höhe von >1 festgesetzt. Somit kann die Zentralbank bei dem Anzeichen eines Inflationsdrucks den Realzins steigen lassen, damit sich das Gleichgewicht wieder herstellen lässt. ^[11] Die Verwendung der erwarteten Inflation auf der rechten Seite dieser Gleichung verdeutlicht, dass als geldpolitisches Instrument zwar nominale Kurzfristzins fungiert, es aber letztendlich um die Beeinflussung des Realzinses geht.

Die Taylor-Regel als eine Weiterentwicklung des IS-LM-Modells

IS-MP-Modell

In der Taylor-Regel sind klassische monetaristisch-keynesianische Elemente und Elemente der „Neuen klassischen Makroökonomik“ miteinander verknüpft. Er setzt den Zins in Abhängigkeit von den Zielabweichungen bei geldpolitisch als relevant erachteten Makrovariablen ein. Das macht im IS-LM-Modell die LM-Bedingung überflüssig, weil dies der rekursiven Bestimmung der nominalen Geldmenge dient. In der neuen Version des IS-LM-Modells messen die Koordinaten den Realzinssatz (y-Achse) und den Realoutput (x-Achse). Der IS-Linie liegen die üblichen Hypothesen zugrunde. Weiterhin reagiert die Gesamtnachfrage gegenläufig zum Realzins. Das hat zur Folge, dass die Lage der Linie durch die Nachfragekomponente bestimmt wird und das güterwirtschaftliche Angebot jederzeit der Nachfrage folgt. Die Lage der neuen MP-Linie (MP=monetary policy) ist abhängig von der aktuellen Inflationsrate und der geldpolitischen Zielrate. Hinsichtlich der Taylor-Regel befolgt die Zentralbank eine einfache Variante. Wenn die Inflationsrate über dem geldpolitischen Zielwert liegt erhöht sie den Realzins (und umgekehrt). Die Bank kennt die erwartete Inflationsrate (durch Annahme rationaler Erwartungen) und steuert diese durch den Nominalzins um den Realzins zu beeinflussen. Dabei orientiert sie sich aber ausschließlich an der aktuellen Inflationsrate. In der Abbildung wird sichtbar, dass zwischen Outputniveau und Inflationsrate stets eine eindeutige und gegenläufige Beziehung besteht.^[12]

Verfahrensschritte zur Herleitung einer zweckmäßigen Regel

Um Abweichungen von den Preis-und Outputzielen zu beeinflussen kann der kurzfristige Zinssatz mittels Herleitung durch einzelne Verfahrensschritte bestimmt werden. Dazu ist die zu prüfende geldpolitische Regel in das gewählte Modell einzufügen und durch die Wahl des möglichen Lösungsalgorithmus aufzulösen. Der nächste Schritt ist die Analyse der stochastischen Verteilung der Varianzen der einzelnen Variablen (Input, Output, Unterbeschäftigung).Schlussendlich folgt die Evaluation der geldpolitischen Regel mit den festen Eigenschaften und der Überprüfung der Robustheit des Modells. Dies kann durch einen Vergleich mit anderen Modellen geschehen. ^[13]

Möglichkeiten der Anwendung der Taylor-Regel

Die Taylor-Regel ist sehr wandelbar und kann somit auf viele verschieden politische Verhältnisse angepasst werden. Dabei kann sie als Grundlage geldpolitscher Entscheidungen angesehen werden. Weiterhin sind auch Modellrechnungen zur Variation der Koeffizienten für die Gewichtung der erwarteten Inflationsrate und des Outputgap möglich.^[14]

Formen der Taylor-Regel

Die ursprüngliche Taylor-Regel

Taylor-Zins und Geldmarktzinsen in den USA von 1995 bis 2002

$r_t=\pi_t \cdot \alpha \cdot (\pi_t-\pi^* ) \cdot \beta \cdot y+r^g$

π_t soll die Inflationsrate und π ^* das Inflationsziel sein, aus dessen Differenz sich die Inflationslücke ergibt. Die Outputlücke wird durch y gekennzeichnet. Als Produktionspotenzial kann die langfristige Entwicklung des BIP bei normaler Auslastung der existierenden Kapazitäten bezeichnet werden. Die Variablen α und β beschreiben wieder die Gleichgewichtsgrößen und der gleichgewichtige Realzins wird durch r^g beschrieben.^[15]

Angewendet auf die FED beschreibt Taylor folgende Regel: r = p + 0,5y + 0,5(p − 2) + 2^[16]

Wird die Gleichung an die von uns bereits genutzten Variablen angepasst, lautet sie folgendermaßen: $i^{Tay}=\pi+0,5(y_t-y_t^* )+0,5(\pi-2)+2$

Die Erwartung, dass die vergangene Inflationsrate mit der zukünftigen Inflationsrate übereinstimmt wird mit π gekennzeichnet. Der Outputgap ($y_t-y_t^*$) ist die Abweichung des langfristigen Wachstumspfades. Der Inflationsgap wird durch die Berechnung der Abweichung der beobachteten Inflationsrate der vergangenen vier Quartale von der angenommenen Zielinflationsrate von 2% bestimmt. Auch die Höhe des kurzfristigen Zinses richtet sich nach dem Inflationsgap (Differenz zwischen aktuellen und der angestrebten Inflationsrate). Wie oben beschrieben sind die Koeffizienten (α und β = 0,5) auch hier die Politik-Reaktions-Parameter.
Aus der Formel lässt sich schließen, je stärker der Outputgap und der Inflationsgap von Zielwert abweichen, desto größer ist der zinspolitische Spielraum der Geldpolitik. Stimmen Inflationsrate und Outputgab mit den Zielwerten überein, besteht keine Abweichung vom langfristigen Wachstumspfad. ^[17] Folglich ergibt sich der Nominalzins aus der Summe des gleichen Realzinses und dem Inflationsziel. Schaut man sich diese Gleichung etwas näher an, kann man feststellen, dass die Realzinsen über den Gleichgewichtswert steigen, wenn das Inflationsziel überschritten wird oder die Kapazitäten überlastet sind. ^[18] Bei den Anzeichen einer überschäumenden Konjunktur werden sich inflationäre Effekte ergeben, bei der sich der Zins erhöhen wird. Befindet sich die Konjunktur jedoch in einer Krise wird dem Rückgang der Inflationsrate gerechnet. Durch die Ausprägung der beiden Gewichten α und β können die unterschiedlichen Zielfunktionen der Zentralbanken verdeutlicht werden. Denn je höher diese ist, umso mehr gehen Abweichungen in die Zinspolitik mit ein.^[19] Konkret impliziert die Taylor-Regel, dass sich bei einem Anstieg der Inflationsrate um einen Prozentpunkt die Federal Funds Rate um 1,5 Prozentpunkte erhöht. Fällt das BIP um einen Prozentpunkt unter das potenzielle BIP ist die Federal Funds Rate um 0,5% Prozentpunkte zu senken. Damit soll bei einem auftretenden Inflationsdruck gewährleistet werden, dass die Geldpolitik restriktiver wird, um somit einen Anstieg des Realzinses zu ermöglichen. Die Taylor-Regel kann somit im positiven und normativen Sinne verstanden werden. Im positiven Sinn liefert die Regel eine Erklärung für die zeitliche Entwicklung eines durch die Zentralbank kurzfristig steuerbaren Zinses. Als eine Handlungsvorschrift der Reaktionsfunktion kann sie im normativen Sinne verstanden werden. ^[20]

Eine allgemeinere Taylor-Regel

(von der Europäischen Zentralbank, Jarchow, Schinke und Schäfer)

i^Tay = r + π_t + α(π_t − π ^* ) + β(y − y ^* )

Der reale Gleichgewichtszinssatz wird mit r beschrieben, die aktuelle Inflationsrate mit π_t und die Zielinflationsrate mit π ^* . Die Produktionslücke (y-y*) ist gleich den vorhergehenden Regeln. Die Politik-Reaktions-Parameter lassen sich je nach Gewichtung der Inflations- und Wachstumskomponente anwenden. Dies können beispielsweise bei starker Gewichtung für α 1,5 und für den Outputkoeffizienten β 0,5 sein. Diese Gewichtung hängt ganz davon ab, welche Priorität den einzelnen Größen beigemessen wird. In der vorliegenden Regel ist der Zinssatz umso größer, je mehr die Inflationsrate den Zielinflationswert übersteigt und je stärker das Produktionspotenzial ausgelastet ist (und umgekehrt). ^[21] Es ist zu erkennen, dass die Volkswirtschaft im Gleichgewicht ist, wenn keine Abweichung des BIP von Produktionspotenzial vorliegt und die Zielinflation der erwarteten Inflation entspricht. Ein Unterschied zur ursprünglichen Taylor-Regel besteht darin, dass der angestrebte Nominalzins nicht aus aktueller Inflation und gleichgewichtigen Realzins bestimmt wird, sondern aus der Zielinflation und dem gleichgewichtigen Realzins. Eine weitere Modifikation zur ursprünglichen Regel besteht darin, dass anstatt der tatsächlichen Inflation die erwartete Inflation eingesetzt wird. Als Begründung ist hierfür die zeitliche Verzögerung zu beachten, die dem Effekt der Geldpolitik auf die Inflation unterliegt. ^[22]

Anwendung der Taylor-Regel für das Euro-Währungsgebiet

(kommt durch die Analyse der Bank für internationalen Zahlungsausgleich(1999) zur Anwendung)

Taylor-Regel angewendet auf das Euro-Währungssystem

i_t = r^eq + π_t + 0,5[y_t + (π ^* − π^ob)]

Der Gleichgewichtszinssatz r^eq wird als konstant angenommen. Die veränderte Inflationsrate gegenüber dem Vorjahr ist π_t. Weiter Bestandteile der Formel sind wie gehabt der Outputgap (y_t), die Zielinflationsrate (π * ) und die aktuelle Inflationsrate (π^ob). Eine vereinfachte Form des allgemeinen, dynamischen Gleichgewichtsmodells zur Darstellung der allgemeinen Konjunkturlage als Funktion von Schocks und zeitlicher Erwartungen lässt sich in zwei Gleichungen darstellen.

Die Gleichung y_t = y₀ − y₁(i_t − E_tπ_{(t + 1)}) + E_ty_{(t + 1)} + v_t beschreibt die Angebotsseite und somit den Output. Das Ziel ist die aktuelle Produktionsentscheidung y_t. In der ersten Klammer wird der Realzinssatz durch den nominalen Zins (i_t) minus der erwarteten Inflationsrate für die kommenden Periode (E_tπ_{(t + 1)}) abgleitet. Die Erwartungen hinsichtlich zukünftiger Produktionsbedingungen (E_ty_{(t + 1)}) haben einen positiven Einfluss auf den nominalen Zinssatz. Mit der Variable v_t wird ein stochastischer Störterm berücksichtigt. Die Parameter y₀ und y₁ sind >0. Mit dieser Gleichung wird die Entwicklung der gesamtwirtschaftlichen Nachfrage bei einer gegebenen politischen Strategie dargestellt.

Für die Inflationsrate ergibt sich π_t = δ₀E_tπ_{(t + 1)} + δ₁(y_t − y ^* ) + u_t, welche der Nachfrageseite entspricht. Die aktuelle Inflationsrate ergibt sich aus Preisanpassungen, welche Aufgrund der Erwartungen für die künftige Inflationsrate vorgenommen werden und dem aktuellen Auslastungsgrad der Kapazitäten (entspricht in etwa der Produktionslücke und einem Störterm). Da nur ein Teil der Unternehmungen Anpassungen vornehmen befinden sich die Werte von δ₀ und δ₁ immer zwischen 0 und 1.

Löst man nun beide Gleichungen nach y_t und π_t auf, so erhält man: i_t = r ^* + π ^* + α(E_tπ_{(t + k)} − π ^* ) Die kurzfristigen Zinsen in der aktuellen Periode wird als r* bezeichnet und die Zielinflation als π * . Der Inflationsgap (E_tπ_{(t + k)} − π ^* ) bezieht sich auf die Abweichung der künftig erwarteten Inflationsrate von der Zielinflationsrate, der mit α gewichtet ist. Da die Formel zu Instabilitäten und willkürlichen Erwartungen führen kann, hält die EZB die Anwendung nicht für empfehlenswert. Ein Grund dafür kann das Steigen des Stabilitätsproblems sein, wenn der Prognosezeitraum k steigt. Es kann angesichts Sensitivität der Geldpolitik extreme Schwankungen der Ergebnisse bewirken. Aus diesem Grund gehen die stabilisierenden Eigenschaften der Taylor-Regel verloren. Aber auch die Veränderung der Erwartungen kann zu konjunkturellen Entwicklungen führen. Folglich ist für Wirtschaftssubjekte unklar, wie das geldpolitische System auf exogene Schocks reagiert. Schlussendlich geht dadurch die Ankerwirkung der Taylor-Regel verloren, die die EZB dazu veranlasst sie nur als Orientierungshilfe zur Erreichung geldpolitscher Ziele zu nutzen. ^[23]

Der Taylor-Zins in Deutschland

Tagesgeldsatz und Taylor-Zins für Deutschland

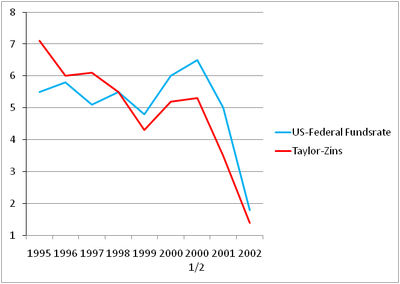
In Deutschland werden Inflationslücke und Produktionslücke mit jeweils 0,5 gleichgewichtet und die Inflationsrate basiert auf dem westdeutschen Preisindex für die Lebenserhaltung. Die bei der Ableitung der Geldmengenziele von der Bundesbank zugrunde gelegten, unvermeidlichen Inflationsrate (bzw. ab 1985 der Preisnorm) dient als Inflationsziel. Die Produktionslücke liegt der Potenzialschätzung der westdeutschen Bundesbank zugrunde. Der gleichgewichtige reale Kurzfristzinssatz wird auf 3,4% gesetzt. Dies stimmt mit dem Durchschnitt des realen Tagesgeldsatzes über den betrachteten Zeitraum von 1. Quartal 1979 bis zum 4. Quartal 1998 überein. Wird die Taylor-Regel angewendet ist bei der Interpretation zu bedenken, dass auch andere Durchschnittswerte vertretbar sind. Auf der Abbildung ist zu sehen, dass der beobachtete Tagesgeldzinssatz glatter als der berechnete Taylor-Zins verläuft. Hätten sich die Bundesbank an den Taylor-Zins orientiert, hätte es ceterus paribus mehr Zinsbewegungen impliziert, als sie mit ihrem Konzept in Wirklichkeit zuließ. Der Grund für die starken Schwankungen ist, dass er negative Konsequenzen einer aktivistischen Geldpolitik nicht berücksichtigt. Trotz allem haben sich beide Zinssätze ähnlich entwickelt. Dabei ist es verwunderlich, dass sie so similar verlaufen, da die Produktionslücke in der Bundesbankpolitik eine große Rolle gespielt hat. Dies ist durch die Gemeinsamkeiten der Taylor-Regel und der Geldmengenstrategie zu erklären. Das heißt, wenn das BIP langsamer als das Produktionspotenzial wächst, stellt die Notenbank durch sinkende Zinsen mehr Geld bereit, als zur Finanzierung des laufenden Wachstums erforderlich wäre.^[24]

Eine Taylor-Regel für das Vereinigte Königreich

(postuliert von Nelson (2000))

i^Tay = i ^* + π ^* + 1,5(π_t − π ^* ) + 1,5(y_t − y ^* )

Der kurzfristige Gleichgewichtszinssatz für ein gleichmäßiges Wachstum wird mit i* und die Zielinflationsrate mit π ^* gekennzeichnet. Der Inflationsgap wird mit einem Politik-Reaktions-Barometer von 1,5 gewichtet. Der Outputgap wird mit 0,5 schwächer gewichtet. ^[25]

Die Berücksichtigung der Wechselkurse

i_t = δ_ππ_t + δ_yy_t + δ_e0e_t + δ_e1e_{(t − 1)} + ρi_{(t − 1)}

Die Inflationsrate wird hier wieder durch π_t dargestellt und der Outputgap durch y_t. Der Parameter et nimmt den Platz für die Wechselkurse ein. Bei Erhöhung bedeutet eine Aufwertung der inländischen Währung. Die politische Einflussnahme spiegeln δ und ρ wider. Eine abnehmende Gewichtung der vergangenen realen Wechselkurse zueinander entspricht der Relation der beiden Koeffizienten. Dies wird durch die Auswirkung der Preisrigiditäten bei Importen und Exporten auf die Inflationsraten verursacht. Laut Taylor spielt es keine große Rolle, ob antizipierte oder aktuelle Inflationsraten genommen werden, weil sie sich zum einen oftmals sehr ähnlich sind und weil antizipierte Inflationsraten von den unterstellten Transmissionsmechanismen abhängen. Gerade für kleine Länder ist es sinnvoll die Wechselkurse zu berücksichtigen, denn die Koeffizienten δ_e0 und δ_e1 hängen von Wechselkursreaktionen politischer Maßnahmen ab.^[26]

Rezeption

Transmissionsmechanismen

1. Die Finanzmarktsicht geht von einer Wirkung der geldpolitischen Maßregeln auf die Renditen Wechselkurswirkungen aus. Die Intensität der Transmissionseffekte über den Außenhandel hängt von der Sensitivität der Wechselkurse ab.
2. Der Kreditkanal, dessen Wirkung darin besteht, die Kreditkosten zu erhöhen oder zu senken. Das kann zu kleinen Varianzen bei der Inflation und dem Output führen.
3. Eine verzögerte Preis-und Lohnanpassung, denn Inflationserwartungen können die zukünftigen Preis-und Lohnanpassungen beeinflussen. ^[27]

Thesen

Treffen ganz oder tendenziell zu:

• je geringer der Inflationsgap (bzw. kleiner Inflationsrate)ist, desto größer ist die Liquiditätszuführung durch EZB
• je kleiner der Outputgap (bzw. je geringer wirtschaftliches Wachstum)ist, desto größer ist die Liquiditätszuführung der EZB
• Preisanpassungen reagieren mit wirtschaftlicher Verzögerung auf Wachstum
• Lohnentwicklung reagiert verzögert auf das wirtschaftliche Wachstum
• kurzfristigen Zinssätze reagieren auf die erwarteten Abweichungen zwischen der Inflationsrate und der Zielinflationsrate
• Taylor-Regel ist zur Beurteilung des geldpolitischen Umfeldes geeignet

Treffen nicht zu:

• Taylor-Regel kann als regelgebundene Form der Geldpolitik anwenden werden
  • trifft nicht beim Euro-Währungssystem zu, denn Schocks erfordern eine diskrete Zinssteuerung
• Anwendung der erwarteten Inflationsraten führen zu besseren Ergebnissen als die aktuellen Inflationsraten
  • laut Taylor spielt es keine ausschlaggebende Rolle, ob die erwartete oder aktuelle Inflationsrate angewendet wird
• Berücksichtigung der Wechselkurse kann zu besseren oder schlechteren Ergebnissen führen
  • bewirkt im Euro-Währungsraum etwas schlechtere Ergebnisse d.h. eine größere Varianz der Zinsen^[28]

Stärken und Schwächen der Taylor-Regel

Stärken

Ein klarer Vorteil der Taylor-Regel ist ihre Einfachheit. Sie bietet eine klare Struktur, um über die Geldmarktpolitik nachzudenken. ^[29]
Des Weiteren bietet sie viele Freiheitsgrade bei der Wahl der Preisvariablen und ist somit flexibel.^[30]
Neben der Preisniveaustabilität bezieht Taylor auch die konjunkturelle Entwicklung mit in die Formel ein. Er geht weiterhin davon aus, dass die Zentralbank nur den kurzfristigen Zins steuert und sich somit die Geldmenge endogen ergibt. ^[31]
Positiv ist auch, dass sie von der Notenbank leicht anzuwenden ist und sich vom privaten Sektor leicht prüfen lässt. Das erleichtert die Kommunikation der geldpolitischen Orientierung.
Die Anhänger der prognosegestützten Version gehen sogar so weit zu behaupten, dass sämtliche relevante Informationen für die Entscheidung vorhanden sind. ^[32]

Schwächen

Eines der größten Probleme ist die Bestimmung des Gleichgewichtszinssatzes. Taylor hat an Stelle des Gleichgewichtszinssatzes die langfristige Wachstumsrate (BIP) der US-Ökonomie eingesetzt. Die beiden sind zwar voneinander abhängig, jedoch nicht gleichzusetzen. Bei der Wachstumsrate des BIP handelt es sich um keinen Zinssatz. Es ist also nicht ausgeschlossen, dass die Zentralbank mit einer anderen Geldpolitik eine andere Wachstumsrate geschaffen hätte. Folglich hätte die Zinspolitik der Notenbank einen anderen Gleichgewichtszins hervorgebracht. Der Zins ist ein Resultat geldpolitscher Entscheidungen und somit keine aus der Realökonomie abgeleitete Größe. Mit dieser Tatsache verliert die Taylor-Regel ihren Anker der Zinsbestimmung und somit auch ihre handlungsanleitende Steuerfunktion.
Auch die Bestimmung der Koeffizienten mit denen die Produktions-und Inflationslücke gewichtete werden ist strittig. Legt eine Zentralbank Wert auf eine strikte Inflationsbekämpfung, so wird sie die Inflationslücke höher bewerten als die Produktionslücke. Die Festlegung einer angemessenen Gewichtung lässt sich nicht korrekt bestimmen, da sie von mehreren Faktoren abhängt, wie z.B. der „Inflationskultur“ oder der Arbeitsmarktkonstellation. Folglich müssen diese Größen geschätzt werden, was sehr riskant sein kann. Es wäre bspw. auch möglich, dass die Gewichtung von der Politik festgelegt werden muss. ^[33]
Weiterhin ist nicht sicher, ob die Inflationslücke auf der Basis des Bip-Deflators oder auf Basis des Preisindex für Lebenserhaltung bestimmt werden soll. Auch die Festlegung der Höhe der Produktionslücke ist nicht unproblematisch. Hier kommt es immer darauf an, welche Methode zur Berechnung verwendet wird. Das Ergebnis wird immer unterschiedlich sein, egal ob man den Log-linearer Trend, den Hodrick-Prescott-Trend oder die Schätzung einer Produktionsfunktion verwendet. Diese werden sich unmittelbar im Niveau und im Verlauf des Taylor-Zinses niederschlagen. ^[34]
Negativ ist auch, dass die Taylor-Regel durch unnötige Schwankungen des Zinssatzes eine höhere Volatilität aufweist. ^[35]
Eine weitere Schwäche besteht darin, dass die Time Lags der zinspolitischen Signale nach den Erfahrungen in vielen Ländern schwer vorauszusehen sind und somit die prozyklische Wirkung nicht auszuschließen ist. ^[36] Auch benötigt bspw. ein Börsencrash kurzfristige monetäre Maßnahmen, was aber nicht zur Folge haben muss, dass die Zentralbank generell von einer geldgebundenen Geldpolitik zu einer diskretionären Geldpolitik zurückkehrt. ^[37] Oder im Fall einer einmaligen Preiserhöhung-wie z.B. infolge einer Erhöhung der Mehrwertsteuer-zeigt sie prinzipiell Handlungsbedarf. ^[38] Auch der verwendete Nominalzins führt zu häufiger Kritik, da er nicht negativ werden kann. Fällt er also auf ein niedriges Niveau, gelingt es der Taylor-Regel nicht mehr, die Bindung des Systems an die geldpolitischen Ziele zu gewährleisten. ^[39]
Weiterhin ist eine Annahme einer Konstanz des realen Zinssatzes kritisch. Dabei sind die zu berücksichtigenden Faktoren dieser Größen die (erwartete) Ertragsrate auf Sachanlagen, die generelle Sparneigung, die allgemeine Einschätzung der Unsicherheiten in der Ökonomie und der Grad der Glaubwürdigkeit der Zentralbank.
Ein wichtiger Punkt, der nicht berücksichtigt wird, ist die Notwendigkeit des vorausschauenden Verhaltens.^[40]

• Michael Woodford: The Taylor Rule and Optimal Monetary Policy. In: The American Economic Review. Vol. 91, No. 2, Papers and Proceedings of the Hundred Thirteenth Annual Meeting of the American Economic Association. (Mai, 2001), S. 232-237.

• Lars E. O. Svensson: What Is Wrong with Taylor Rules? Using Judgment in Monetary Policy through Targeting Rules. In: Journal of Economic Literature. Bd. 41 Nr. 2 (Juni 2003), S. 426-477.

Belege

1. ↑ Michael Heine, Hansjörg Herr: Die Europäische Zentralbank. Eine kritische Einführung in die Strategie und Politik der EZB. Marburg 2004, ISBN 3-89518-455-1, S. 150.
2. ↑ John B. Taylor: An Historical Analysis of Monetary Policy Rules. Working Paper 6768, Cambridge, USA, October 1998, S. 51-52. Abgerufen am 25. November 2010
3. ↑ vgl. Ralph Anderegg: Grundzüge der Geldtheorie und Geldpolitik. München 2007, ISBN 978-3-486-58148-5, S. 313.
4. ↑ vgl. Klaus Schaper (2001), S. 138.
5. ↑ Johannes Treu: Der Taylorzins und die europäische Geldpolitik 1999-2009. Moritz-Arndt-Universität Greifswald/Rechts- und Staatswissenschaftliche Fakultät 2010, ISSN 1437-6989, S. 2-3. Abgerufen am 16. November 2010.
6. ↑ Vgl. Ralph Anderegg, (2007), S. 313.
7. ↑ Vgl. Michael Heine, Hansjörg Herr, (2004), S. 150.
8. ↑ Christian Peukert: Die Taylor Regel. Übung zur empirischen Wirtschaftsforschung, Ulm 2010, S. 2-3. Abgerufen am 26. November 2010.
9. ↑ Vgl. Michael Heine, Hansjörg Herr, (2004), S.150, 151.
10. ↑ Egon Görgens, Franz Seitz, Karlheinz Ruckriegel: Europäische Geldpolitik. Theorie, Empire, Praxis. 4. überarbeitete Auflage. Stuttgart 2004, ISBN 3-8252-8285-6, S. 228-229.
11. ↑ .Europäische Zentralbank.. Monatsbericht Oktober 2001 S. 46. Abgerufen am 29. November 2010
12. ↑ Franco Reither: Grundzüge der Neuen Keynesianischen Makroökonomik. Hamburg 2003, S. 2-3. Abgerufen am 27. November 2010
13. ↑ Vgl. Ralph Anderegg, (2007), S. 322-323.
14. ↑ Vgl. Ralph Anderegg, (2007), S. 322.
15. ↑ Johannes Treu: Der Taylorzins und die europäische Geldpolitik 1999-2009. Moritz-Arndt-Universität Greifswald/Rechts- und Staatswissenschaftliche Fakultät 2010, ISSN 1437-6989, S. 3. Abgerufen am 16. November 2010.
16. ↑ John B. Taylor: Discretion versus policy rules in practice. In: Carnegie-Rochester Conferences Series on Public Policy. 39 (1993). S. 202. Abgerufen am 27. November 2010
17. ↑ Vgl. Ralph Anderegg, (2007), S. 316.
18. ↑ Vgl. Egon Görgens, Franz Seitz, Karlheinz Ruckriegel (2004). S. 245.
19. ↑ Vgl. Michael Heine, Hansjörg Herr, (2004), S. 151
20. ↑ Johannes Treu: Der Taylorzins und die europäische Geldpolitik 1999-2009. Moritz-Arndt-Universität Greifswald/Rechts- und Staatswissenschaftliche Fakultät 2010, ISSN 1437-6989, S. 3-5. Abgerufen am 16. November 2010.
21. ↑ Vgl. Ralph Anderegg, (2007), S. 316, 317
22. ↑ Johannes Treu: Der Taylorzins und die europäische Geldpolitik 1999-2009. Moritz-Arndt-Universität Greifswald/Rechts- und Staatswissenschaftliche Fakultät 2010, ISSN 1437-6989, S.7-9. Abgerufen am 16. November 2010.
23. ↑ Vgl. Ralph Anderegg, (2007), S. 217-319
24. ↑ .Deutsche Bundesbank: Taylor-Zins und Monetary Conditions Index.. Monatsbericht April 1999. S. 51-52. Abgerufen am 28. November 2010
25. ↑ Vgl. Ralph Anderegg, (2007), S. 317
26. ↑ Vgl. Ralph Anderegg, (2007), S. 319, 320.
27. ↑ Vgl. Ralph Anderegg, (2007), S. 322.
28. ↑ Vgl. Ralph Anderegg, (2007), S. 324, 325.
29. ↑ PeterBofinger, Julian Reischle, Andrea Schächter: Monetary Policy. Goals, Institutions, Strategies, and Instruments. New York 2001, ISBN 0-19-924057-4, S. 274.
30. ↑ Deutsche Bundesbank: Taylor-Zins und Monetary Conditions Index. Monatsbericht April 1999. S. 50. Abgerufen am 28. November 2010
31. ↑ Vgl. Michael Heine, Hansjörg Herr, (2004), S. 153.
32. ↑ .Europäische Zentralbank.. Monatsbericht Oktober 2001 S. 47. Abgerufen am 29. November 2010
33. ↑ Vgl. Michael Heine, Hansjörg Herr, (2004), S. 153-155.
34. ↑ .Deutsche Bundesbank: Taylor-Zins und Monetary Conditions Index.. Monatsbericht April 1999. S. 50. Abgerufen am 28. November 2010
35. ↑ Vgl. Michael Heine, Hansjörg Herr, (2004), S. 153-155.
36. ↑ Klaus Schaper: Makroökonomie. Ein Lehrbuch für Sozialwissenschaftler. Frankfurt/Main 2001, ISBN 3-593-36733-5, S. 139.
37. ↑ Vgl. Ralph Anderegg, (2007), S. 325.
38. ↑ Deutsche Bundesbank: Taylor-Zins und Monetary Conditions Index.. Monatsbericht April 1999. S. 50. Abgerufen am 28. November 2010
39. ↑ .Europäische Zentralbank.. Monatsbericht Oktober 2001 S. 49. Abgerufen am 29. November 2010
40. ↑ Deutsche Bundesbank: Taylor-Zins und Monetary Conditions Index. Monatsbericht April 1999. S. 50. Abgerufen am 28. November 2010