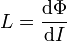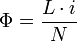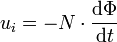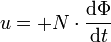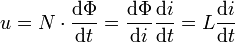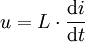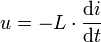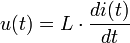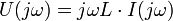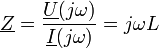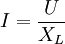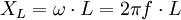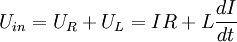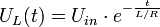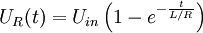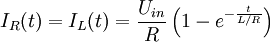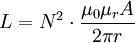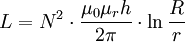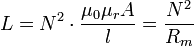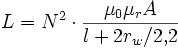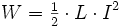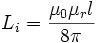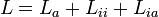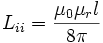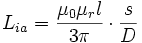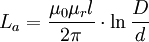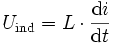Induktiver Widerstand

Die Induktivität (auch Eigeninduktivität oder Selbstinduktion) ist eine elektrische Eigenschaft eines stromdurchflossenen elektrischen Leiters aufgrund des Magnetfeldes, das ihn durch den Stromfluss umgibt. Sie ergibt sich aus dem Verhältnis des mit dem Leiter verketteten magnetischen Flusses Φ und der Stromstärke:

$L = \frac{\mathrm{d}\Phi}{\mathrm{d}I}$

Eine Wirkung der Eigeninduktivität ist z. B. die Selbstinduktionsspannung entlang der Leiterschleife, wenn sich der durchfließende Strom ändert. Des Weiteren wird zwischen innerer und äußerer Induktivität unterschieden.

Zweipole und elektrische Verbraucher werden als induktiv bezeichnet, wenn ein sie durchfließender, zeitlich veränderlicher Strom über deren Klemmen eine zur Änderungsgeschwindigkeit proportionale Spannung hervorruft. Andere verwandte Anwendungsgebiete, in denen die Induktivität eine indirekte Rolle spielt, sind elektrische Maschinen wie beispielsweise Transformatoren oder Elektromotoren.

Elektrische induktive Bauelemente, die eine feste oder variable Induktivität aufweisen, gehören zu den sogenannten passiven Bauelementen. Sie werden im deutschen Sprachraum von der Elektronikindustrie ebenfalls unter dem Oberbegriff Induktivität zusammengefasst. Für die elektrische Energieversorgung gehören dazu die Drosseln und Transformatoren, für die Datentechnik sind es Spulen, Übertrager und Baluns. Sie können unter Umständen sehr große Abmessungen erreichen. Induktive Bauelemente mit festem Induktivitätswert für elektronische Schaltungen, wenn sie in bedrahteter Form ausgeführt sind, heißen Festinduktivitäten (DIN EN 61605). Wenn sie in oberflächenmontierbarer Form (SMD) ausgeführt sind, heißen sie Chipinduktivitäten (DIN EN 62024-1). Induktive Bauelemente mit einstellbarem Induktivitätswert sind Abgleichspulen. Weitere Begriffe siehe auch: Kategorie:Induktanz).

Definition

Wenn ausschließlich magnetische Stoffe mit einer konstanten Permeabilitätszahl in der Umgebung des Stromkreises vorhanden sind, dann folgt aus dem Durchflutungsgesetz, dass die magnetische Flussdichte B dem Strom i in einer Leiterschleife proportional ist. Daher ist auch der insgesamt vom Strom i erzeugte magnetische Fluss Φ direkt proportional dem Momentanwert der Stromstärke i. Der dabei auftretende Proportionalitätsfaktor bei N Windungen wird als Induktivität L bezeichnet:

$\Phi = \frac{L \cdot i}{N}$

Die Maßeinheit für die Induktivität ist im SI-Einheitensystem das Henry, benannt nach dem US-amerikanischen Physiker Joseph Henry. Abgekürzt wird die Einheit mit H.

Betragsmäßig liegt eine Induktivität von 1 H dann vor, wenn bei gleichförmiger Stromänderung von einem Ampere in einer Sekunde eine Selbstinduktionsspannung von einem Volt entlang des Leiters entsteht. $1\mathrm{H}=1 \frac{\mathrm{V}\cdot\mathrm{s}}{\mathrm{A}}$

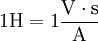
Anmerkung: Weisen die magnetischen Stoffe wie Eisen in der Nähe des elektrischen Leiters keine konstante Permeabilitätszahl μ_r auf (diese ist beispielsweise von der magnetischen Flussdichte B abhängig), dann ist die Induktivität kein konstanter Proportionalitätsfaktor sondern eine Funktion L(B) der magnetischen Flussdichte. Dies wird auch als Sättigungsmagnetisierung bezeichnet. Es ergeben sich nichtlineare Induktivitäten, die analytisch wesentlich schwieriger zu behandeln sind.

Induktion

Dem Induktionsgesetz entsprechend ergibt sich die Umlaufspannung u_i einer N-fach um den magnetischen Fluss Φ geführten geschlossenen (Leiter)schleife aus der zeitlichen Änderungsrate des durch diese Schleife hindurchtretenden magnetischen Flusses Φ:

$u_i = - N \cdot \frac{\mathrm{d}\Phi}{\mathrm{d}t}$

Das dabei auftretende negative Vorzeichen leitet sich direkt aus den Maxwellgleichungen (Induktionsgesetz) ab und beruht auf der Konvention, dass das magnetische Feld rechtshändig zum Integrationsweg und zum elektrischen Feld steht.

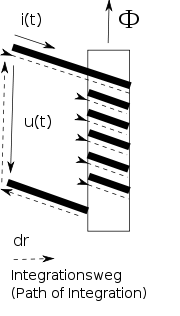
In der Netzwerktheorie interessiert nicht das Kreisintegral der Spannung, sondern vielmehr die an den Klemmen messbare Klemmenspannung. Der Zusammenhang zwischen der induzierten Spannung U_i und der Klemmenspannung u(t) wird anhand der beigefügten Abbildung erläutert:

Zusammenhang von Selbstinduktionsspannung und Klemmenspannung

Integriert man das elektrische Feld 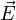$\vec E$ über den mit gestrichelten Linien eingezeichneten geschlossenen Weg r, so addieren sich die in den Spulenwicklungen abfallenden Spannungen mit der Klemmenspannung. Nimmt man ideal leitfähige Spulenwicklungen an, so fällt die induzierte Spannung 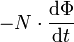$- N \cdot \frac{\mathrm{d}\Phi}{\mathrm{d}t}$ aufgrund der Feldfreiheit in den Spulenwicklungen komplett an den Spulenklemmen ab. Die Richtung dieser Spannung entspricht dem gewählten Integrationsweg und verläuft im Beispiel "von unten nach oben".

Daraus ergibt sich für die im Bild "von oben nach unten" eingezeichnete Klemmenspannung u:

$u = +N \cdot \frac{\mathrm{d}\Phi}{\mathrm{d}t}$

Mit der obigen Definition der Induktivität lässt sich die Beziehung von Spannung u als Funktion des Stromes i als Differentialgleichung ausdrücken:

$u = N \cdot \frac{\mathrm{d}\Phi}{\mathrm{d}t} = \frac{\mathrm{d}\Phi}{\mathrm{d}i} \frac{\mathrm{d}i}{\mathrm{d}t} = L \frac{\mathrm{d}i}{\mathrm{d}t}$

Der dabei auftretende magnetische Fluss Φ ist jener Fluss, der erst durch den Strom i durch die Leiterschleifen erzeugt wird. Weitere externe magnetische Flüsse durch die Leiterschleifen sind in diesem Fall als nicht vorhanden angenommen bzw. zeitlich konstant. Die Spannung u nennt man die bei Selbstinduktion auftretende Klemmenspannung.

Verbraucherzählpfeilsystem

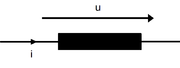
Das Vorzeichen in obiger Gleichung ist abhängig von der Zählrichtung von Strom und Spannung. Stimmt die Richtung der Spannung u mit der Richtung des Stromes entlang der Leiterschleife überein, wie in nebenstehender Grafik dargestellt, spricht man vom sogenannten Verbraucherzählsystem, und es gilt:

$u = L \cdot \frac{\mathrm{d}i}{\mathrm{d}t}$

Sind die Richtungen von Spannung u Strom i entlang der Leiterschleife entgegengesetzt gerichtet, spricht man vom sogenannten Erzeugerzählpfeilsystem, und es gilt:

$u = -L \cdot \frac{\mathrm{d}i}{\mathrm{d}t}$

Man bezeichnet diesen bei Stromänderung entstehenden Spannungsabfall u dann als Selbstinduktionsspannung oder induktiven Spannungsabfall. Die obige Differentialgleichung ist die Elementgleichung, mit der sich lineare Induktivitäten, wie beispielsweise Spulen in elektrischen Schaltungen, beschreiben lassen.

Induktiver Widerstand

Transformiert man die Differentialgleichung

$u(t) = L \cdot \frac{di(t)}{dt}$

in den Laplace-Bereich mit der unabhängigen Variablen s = σ + jω = jω, so wird aus dem Differentialoperator d / dt der Faktor jω, und es gilt:

$U(j\omega) = j \omega L \cdot I(j \omega)$

Das Zeichen ω bezeichnet die Kreisfrequenz ω = 2πf. Ähnlich wie beim Ohmschen Gesetz lässt sich für die Spule daraus ein Wechselstromwiderstand

$\underline{Z} = \frac{\underline U(j\omega)}{\underline I(j\omega)} = j \omega L$

definieren, der auch als (komplexe) Impedanz bezeichnet wird.

In sehr einfachen Schaltungen kann man Wechselstromrechnungen auch ohne komplexe Zahlen durchführen. Wird eine Induktivität an eine Wechselspannung vom Betrag U gelegt, kann der Betrag I des Stromes nach der Formel

$I=\frac{U}{X_L}$

berechnet werden, wobei für den induktiven Widerstand X_L bei der Frequenz f gilt

$X_L=\omega \cdot L=2\pi f\cdot L$

Zeitkonstante

Das Bild zeigt die typische Anwendung einer Induktivität als Teil einer elektrischen Schaltung. Zum Initialzeitpunkt (Startzeitpunkt t=0) wird die Spannung U_in an die Reihenschaltung eines Widerstandes R und einer Spule L gelegt. Nach den Gesetzmäßigkeiten von Reihenschaltungen gilt für die Spannung der Zusammenhang:

$U_{in}=U_R + U_L = IR + L\frac{dI}{dt}$

Die Differentialgleichung liefert die Lösungen

$\,\!U_L(t) = U_{in}\cdot e^{-\frac{t}{L/R}}$

$\,\!U_R(t) = U_{in}\left(1 - e^{-\frac{t}{L/R}}\right)$

$\,\!I_R(t) =I_L(t) = \frac{U_{in}}{R}\left(1 - e^{-\frac{t}{L/R}}\right)$

Den Quotienten L/R nennt man Zeitkonstante τ (griechisch: tau), die angibt

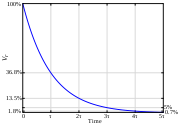
• zu welchem Zeitpunkt nach dem Einschalten die Spannung U_L an der Induktivität nur noch 36,8 % der Anfangsspannung U_in beträgt
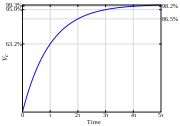
• zu welchem Zeitpunkt nach dem Einschalten der Strom I_L durch die Induktivität auf 63,2 % des Endwertes U_in/R gestiegen ist.

Die Zeitkonstante ist Ursache, dass bei großen Induktivitäten geraume Zeit vergehen kann, bis der Strom (und damit das erzeugte Magnetfeld) seinen Nennwert erreicht. Entgegen aller Intuition wird diese Zeit geringer, wenn R größer wird. Dieser Widerstand kann der Innenwiderstand des Netzgerätes sein oder auch der Widerstand des Drahtes, aus dem die Induktivität gefertigt wurde.

Die Abnahme der Zeitkonstanten mit zunehmendem Widerstand ist auf den abnehmenden Nennwert zurückzuführen. Die anfängliche Stromanstiegsgeschwindigkeit (U / L) ist unabhängig vom Widerstand.

Die größte Zeitkonstante hat natürlich eine Induktivität, deren Magnetfeld ganz im (ungesättigten) Eisen verläuft. Große Transformatoren haben bei zweckmäßiger (gleiche Stromdichte in allen Wicklungen) Parallelschaltung der Wicklungen eine Zeitkonstante von vielen Minuten, nicht etwa Sekunden. Bei der Messung des ohmschen Wicklungswiderstandes ist äußerste Vorsicht geboten.

Spannung UL an der Induktivität L als Funktion der Zeit (engl. time)

Spannung UR am Vor-Widerstand als Funktion der Zeit. Die gleiche Funktion gilt für den Strom IL durch die Spule als Funktion der Zeit

Hinweis: in den verwendeten Abbildungen wird das angloamerikanische Symbol V statt dem deutschen U für die elektrische Spannung verwendet.

Beispiel

An eine Spule mit L = 0,5 H und einem Wicklungswiderstand R = 20 Ω wird bei t=0 s. eine Spannung U_in = 40 V gelegt. Aus der Zeitkonstante τ = L/R = 25 ms und den Zeitangaben im Bild folgt, dass der Strom durch die Spule nach 3τ = 75 ms erst 95 % des Endwertes 2 A erreicht.

Induktivitätsbestimmung verschiedener Leiteranordnungen

Durch Anwendung der Berechnungsmethoden für magnetische Felder, insbesondere des Biot-Savart-Gesetzes, lassen sich für einige einfache geometrische Leiteranordnungen die äußeren Induktivitäten analytisch bestimmen. Kompliziertere Leiteranordnungen sind in der Feldberechnung meist nur noch mittels numerischer Berechnungsverfahren zugänglich.

Die im Folgenden näher dargestellten Leiteranordnungen haben auch technische Bedeutung, mit dem Ziel, elektrische Bauteile mit definierter und bekannter Induktivität herzustellen. Diese Bauelemente werden Spulen oder Drossel genannt.

Induktivität einer Ringspule

Eine Ringspule, auch als Toroidspule bezeichnet, besteht aus einem Ring mit dem mittleren Radius r und Querschnittsfläche A aus einem magnetisch gut leitfähigen Material mit hoher relativer Permeabilitätszahl µ_r, wie beispielsweise einem Ferrit gebildet. Die dabei auftretende Naturkonstante µ₀ ist die magnetische Feldkonstante.

Dieser ringförmige Kern wird mit einem dünnen Draht mit N Windungen bewickelt. Die Induktivität L ist dann in Näherung gegeben in der Form:

$L = N^2 \cdot \frac{\mu_0\mu_r A}{2 \pi r}$

Eine bessere Näherung für die Induktivität einer Ringspule, welche die Abhängigkeit der magnetischen Feldstärke als Funktion des Radius beachtet, lautet:

$L = N^2 \cdot \frac{\mu_0\mu_r h}{2 \pi} \cdot \ln \frac{R}{r}$

Dabei wird ein rechteckförmiger Querschnitt des Ringes mit der Höhe h angenommen. Der äußere Radius des Kerns ist mit R und der Innenradius mit r bezeichnet.

In allen Fällen gilt, dass diese Gleichungen nur bei hinreichend dünnem Draht gute Näherungsergebnisse liefern.

Induktivität einer Zylinderspule

Bei einer zylinderförmigen Spule, deren Länge l sehr groß gegenüber dem Durchmesser des Querschnitts A ist, lässt sich die Induktivität folgendermaßen bestimmen:

$L = N^2 \cdot \frac{\mu_0 \mu_r A}{l} = \frac{N^2}{R_m}$

Dabei wird neben der Voraussetzung eines dünnen elektrischen Leiters der magnetische Widerstand des Außenraumes vernachlässigt und nur R_m des Kerns angenommen. Diese Gleichung gilt also ebenfalls nur in Näherung. In der Praxis wird der Ausdruck daher meist mit einem empirisch ermittelten und tabellierten Spulenfaktor f multipliziert, der im Bereich von 0…1 liegt und die Streuverluste im Außenraum der Spule beachtet.

Für kürzere Zylinderspulen existieren Approximationsformeln, die die endliche Länge der Spule und damit die „schlechtere“ magnetische Feldführung in ihrem Inneren berücksichtigen. Für eine Spule, deren Länge noch mindestens das 0,6-fache des Radius beträgt, gilt (r_w: Windungsradius)

$L = N^2 \cdot \frac{\mu_0\mu_r A}{l+2 r_w/2{,}2}$

Bestimmung der Induktivität mittels A_L-Wert

In der Praxis werden oft fertige Spulenkerne verwendet, für die häufig vom Hersteller eine Induktivitätskonstante A_L (Al-Wert, meist in nH) angegeben wird. In diesem Wert sind bereits alle Materialkonstanten und die spezielle Geometrie der Anordnung als Näherung zusammengefasst. Wenn man den Kern mit N Windungen bewickelt, erhält man eine Spule mit der Induktivität:

$L = A_{L} \cdot N^{2}$.

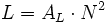Feldenergie

Induktive Bauelemente wie Spulen speichern Energie in Form ihres Magnetfeldes. Das Magnetfeld einer Spule der Induktivität L, die vom Momentanwert des Stromes I durchflossen wird, enthält die Energie W:

$W = \tfrac{1}{2} \cdot L \cdot I^2$

Bei einer plötzlichen Unterbrechung des Stromkreises, muss sich die in der Spule gespeicherte Energie in sehr kurzer Zeit umsetzen und ergibt an den Anschlussklemmen eine sehr hohe Selbstinduktionspannung, die zu Beschädigungen an der Isolation oder anderen Schaltungsteilen führen kann. Um dies zu vermeiden, werden induktive Bauelemente vor dem Abschalten meist mit einem Lastwiderstand kurzgeschlossen, in dem sich die im magnetischen Feld gespeicherte Energie thermisch umsetzt. Diese hohe Spannung kann aber auch zur Versorgung von elektrischen Bauteilen mit hohem Spannungsbedarf, wie etwa eine Zündkerze, verwendet werden.

Andere Methoden zur thermischen Umsetzung bei Umschaltvorgängen sind die in Gleichspannungskreisen verwendeten Schutzdioden.

Innere und äußere Induktivität

Der Begriff Äußere Induktivität wird für den Beitrag des im Raum außerhalb des elektrischen Leiters auftretenden magnetischen Flusses zur Induktivität verwendet. In obigen Beispielen zur Bestimmung der Induktivität verschiedener geometrischer Leiteranordnungen wurden die Querschnitte der elektrischen Leiter als vernachlässigbar dünn angenommen. In diesem Fall kann sich die Bestimmung der Induktivität auf die Bestimmung der äußeren Induktivität bzw. einer idealisierten Feldform beschränken.

Besitzt der elektrische Leiter (Draht) hingegen eine nicht vernachlässigbare räumliche Ausdehnung, eine entsprechende Querschnittsfläche, tritt auch eine magnetische Flussdichteverteilung innerhalb des Leiters auf. Die davon abgeleitete Induktivität wird als innere Induktivität bezeichnet. Im einfachsten Fall einer gleichmäßigen Stromverteilung über den Querschnitt des Leiters mit der Länge l lässt sich die innere Induktivität mit folgender Gleichung bestimmen:

$L_i = \frac{\mu_0 \mu_r l}{8 \pi}$

Bemerkenswert daran ist, dass die innere Induktivität nicht von den konkreten geometrischen Abmessungen wie Durchmesser der Querschnittsfläche des Leiters abhängt. Jener Ausdruck gilt nur bei gleichmäßiger Stromverteilung, also nur bei Gleichstrom, und nur wenn die Querschnittsfläche des Leiters keine inneren Begrenzungen aufweist. Ist die Stromverteilung aufgrund des Skineffektes bei höheren Frequenzen nicht mehr gleichmäßig, ergeben sich andere, komplexere Ausdrücke für die frequenzabhängige innere Induktivität. Die inneren Induktivitäten sind wegen der Stromverdrängung im Leiter stark frequenzabhängig und nehmen mit steigender Frequenz ab.

Die innere Induktivität ist vor allem bei der Bestimmung der Gesamtinduktivität von elektrischen Kabeln von Bedeutung, da bei diesen bei niedrigen Frequenzen (z.B. Netzfrequenz) die Leiterquerschnitte oft nicht vernachlässigt werden können.

Induktivität einer Koaxialleitung

Zur Bestimmung der Induktivität eines Koaxialkabels der Länge l (sog. Induktivitätsbelag) sind bei niedrigen Frequenzen die inneren Induktivitäten des inneren Leiters L_ii und des äußeren Leiters L_ia zu berücksichtigen. Hauptsächlich wirkt jedoch die Induktivität L_a des konzentrischen Raumes zwischen den beiden Leitern. Die gesamte Induktivität einer koaxialen Leitung der Länge l ergibt sich aus der Summe der einzelnen Teilinduktivitäten:

$\;L = L_a + L_{ii} + L_{ia}$

Im Gleichstromfall kann für den inneren Leiter mit dem Durchmesser d obiger Ausdruck für die innere Induktivität verwendet werden:

$L_{ii} = \frac{\mu_0 \mu_r l}{8 \pi}$

Die ebenfalls stark frequenzabhängige innere Induktivität des äußeren Leiters mit der Dicke s und den Innendurchmesser D, der als Kreisring konzentrisch angeordnet ist, kann im Gleichstromfall in guter Näherung bestimmt werden zu:

$L_{ia} = \frac{\mu_0 \mu_r l}{3 \pi} \cdot \frac{s}{D}$

Die frequenzunabhängige äußere Induktivität im Dielektrikum ist bei Koaxialkabeln:

$L_a = \frac{\mu_0 \mu_r l}{2 \pi} \cdot \ln \frac{D}{d}$

Bei höheren Frequenzen, ab 10 kHz aufwärts, können die beiden Terme der inneren Induktivität wegen des Skineffektes vernachlässigt werden. Für die Bestimmung des Wellenwiderstandes eines Koaxialkabels bei typischen Frequenzen ist daher nur der Summand L_a der äußeren Induktivität von wesentlicher Bedeutung.

Gegeninduktivität

Die Gegeninduktivität kennzeichnet die gegenseitige magnetische Einwirkung zweier oder mehrerer räumlich benachbarter Stromkreise. Sie wird auch als magnetische Kopplung bezeichnet. Die wichtigste technische Anwendung findet die Gegeninduktivität bei einem Transformator.

Nichtlineare Induktivität

Die relative Permeabilitätszahl μ_r hängt als Stoffkonstante nicht nur von dem jeweiligen Material ab, sondern ist bei vielen Materialien auch von der magnetischen Flussdichte abhängig. Bei hohen magnetischen Flussdichten kommt es zu einer sogenannten magnetischen Sättigung der Materialien und als Folge einer Reduktion der relativen Permeabilitätszahl μ_r bis auf 1. Dadurch ist die Induktivität direkt von der magnetischen Flussdichte abhängig, die ihrerseits meist eine Funktion des durch die Spule fließenden elektrischen Stromes ist. Somit ändert sich die Induktivität einer Spule in Abhängigkeit vom Momentanwert des Stromes, der durch die Spule fließt.

Die Folge davon ist, dass bei nichtlinearen Induktivitäten in Wechselspannungsanwendungen zusätzliche Oberschwingungen als nichtlineare Verzerrungen auftreten können. Auch sind bei Berechnungen mit nichtlinearen Induktivitäten die einfachen Methoden der (linearen) komplexen Wechselstromrechnung nicht mehr direkt anwendbar.

Die Nichtlinearität von Induktivitäten kann erwünscht sein, z. B. bei Speicherdrosseln in Schaltreglern, um diese besser an verschiedene Lastfälle anzupassen, oder in den Ablenkschaltungen von Fernsehempfängern, um dem nichtlinearen Stromverlauf in den Ablenkspulen entgegen zu wirken. Auch bei den sogenannten Sättigungsdrosseln zur Entstörung von Thyristorstellern ist Nichtlinearität erwünscht.

Messgeräte

Induktivität kann nicht direkt gemessen werden. Es kann lediglich ihre Auswirkung gemessen werden.

Durch Aufschalten einer bekannten Wechselspannung und Messung des durch das induktive Bauelement fließenden Wechselstromes (oder umgekehrt) kann über die Reaktanz die Induktivität ermittelt werden. Dazu werden Amplitude und Phasenlage bestimmt. Diese Methode wird in einfachen Labormessgeräten angewendet und liefert den Induktivitätswert, die Güte sowie den Wert eines äquivalenten Serien- oder Parallelwiderstandes.

Durch Parallelschalten einer bekannten Kapazität zur Induktivität erhält man einen Schwingkreis. Ermittelt man dessen Resonanzfrequenz, kann man daraus auf die Induktivität schließen. Diese Methode ist auch ohne spezielle Geräte durchführbar und daher unter Bastlern und Amateuren weit verbreitet. Die Genauigkeit ist recht hoch.

Für hohe Genauigkeiten wird eine Messbrücke verwendet: Maxwell-Brücke. Diese Methode ist sehr genau und wird u. a. in der automatisierten Fertigung von Spulen eingesetzt.

Beim Bestimmen der Induktivitäten realer Spulen muss beachtet werden, dass je nach Spulenkonstruktion zu sehr hohen Frequenzen hin die kapazitive Kopplung der Windungen und Lagen wirksam wird. Der Impedanzverlauf steigt bis zu einem Maximalwert und bekommt Schwingkreischarakter, um zu noch höheren Frequenzen hin wieder zu sinken – die Spule stellt dann eine Kapazität dar.

Induktivität als störende Eigenschaft

Jeder elektrische Strom verursacht ein Magnetfeld (Elektromagnetismus), in dem magnetische Energie gespeichert ist. Somit besitzt jedes Stück eines elektrischen Leiters eine kleine Induktivität. Auf Leiterplatten kann als Überschlagsrechnung mit einer Induktivität von rund 1,2 nH pro Millimeter Leitungslänge gerechnet werden. Zusammengefasst ergeben diese Induktivitäten die parasitäre Aufbauinduktivität einer elektrischen Schaltung.

Die Magnetfelder von nahe beieinander liegenden Leiterstücken beeinflussen sich durch die magnetische Kopplung dann gegenseitig. Liegen z. B. Hin- und Rückleitung eines Stromkreises sehr eng beieinander, heben sich deren Magnetfelder gegenseitig teilweise auf, was die Gesamtinduktivität dieser Anordnung stark verringert. Daher werden oft Strompfade eng aneinander geführt und Kabel miteinander verdrillt.

Soll sich der Strom in einer induktiven Leiterschleife ändern, muss eine zur Stromänderungsgeschwindigkeit di/dt proportionale Spannung U_ind wirksam sein:

$U_\mathrm{ind} = L \cdot \frac{\mathrm{d}i}{\mathrm{d}t}$

Häufig zum Schalten von Lasten mit induktivem Verhalten benutzte Schalter und Relais weisen deswegen deutliche Abnutzungsspuren an den Kontakten auf, die deren Funktion stark beeinträchtigen können: beim Abschalten fließt der Strom aufgrund der Induktivität weiter und bildet einen Lichtbogen (siehe Schaltlichtbogen), in den sich die in der Induktivität gespeicherte Energie entlädt. Noch kritischer sind Stromflussänderungen, die durch Halbleiterschalter hervorgerufen werden. Halbleiterbauteile werden von derart hohen Spannungen oft zerstört. Daher muss bei der Konstruktion von Schaltungen mit hohen Stromänderungsgeschwindigkeiten auf einen niederinduktiven Aufbau geachtet werden. Zusätzlich werden häufig Snubber-Netzwerke am Halbleiter angebracht. Falls möglich und nötig, werden auch Freilaufdioden benutzt. Neuere Halbleiterschalter können oft auch ohne Schutzbeschaltung induktive Lasten schalten, indem der Energieabbau in einem kontrollierten Avalanchedurchbruch erfolgt.

Ein weiteres Problem parasitärer Induktivitäten ist die Interaktion mit parasitären Kapazitäten. Der dadurch entstandene Schwingkreis kann störende Spannungsschwingungen erzeugen, die Halbleiterbauteilen schaden können und die Elektromagnetische Verträglichkeit und die Signalübertragungseigenschaften verschlechtern.

Literatur

• Frederick W. Grover: Inductance Calculations: Working Formulas and Tables. Reprint Auflage. Dover Publications, New York 1952. 
• Karl Küpfmüller, Gerhard Kohn: Theoretische Elektrotechnik und Elektronik. Eine Einführung. 14. Auflage. Springer-Verlag, Berlin 1993, ISBN 3-540-56500-0. 
• Otto Zinke, Heinrich Brunswig: Hochfrequenztechnik I. Hochfrequenzfilter, Leitungen, Antennen. 5. Auflage. Springer-Verlag, Berlin 1995, ISBN 3-540-58070-0. 
• Howard Johnson: High-Speed Digital Design. Prentice-Hall, New Jersey 1993, ISBN 0-13-395724-1.