- Vergrößerungsfunktion
-
Die Vergrößerungsfunktion gibt im eingeschwungenen Zustand den Zusammenhang zwischen der Eingangs- und Ausgangsamplitude eines Schwingungssystems in Abhängigkeit der Erregerfrequenz an. Sie ist ein Begriff aus der Maschinendynamik. Die Vergrößerungsfunktion wird auch als Amplituden-Frequenzgang des Systems bezeichnet.[1] Amplitudengang und Vergrößerungsfunktion können sich durch einen geeignet gewählten Normierungsfaktor unterscheiden. Um die Vergrößerungsfunktion unabhängig von einem speziellen Schwingungssystem zu machen, wird auch die Erregerfrequenz auf die ungedämpfte Eigenfrequenz bezogen. Der Vergrößerungsfaktor oder Verstärkungsfaktor ist der Wert der Vergrößerungsfunktion bei einer bestimmten Frequenz.[2]
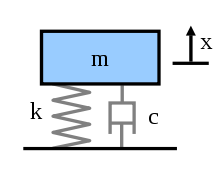
Ein lineares gedämpftes Schwingungssystem z. B. ein Masse-, Feder-, Dämpfer-System kann durch eine periodische Kraft, die auf die Masse wirkt angeregt werden. Die Kraftamplitude stellt die Eingangsamplitude dar. Die Vergrößerungsfunktion zwischen der Ausgangsamplitude x und der Eingangsamplitude lautet dann (siehe Herleitung):
Dabei bezeichnet:
- η das Frequenzverhältnis ω / ω0,
- D die Lehrsche Dämpfung,
- ω die Erregerkreisfrequenz,
- ω0 die ungedämpfte Eigenkreisfrequenz, auch Kennkreisfrequenz genannt.
Bei ω0 hat der Phasengang den Wert −90° (Phasenresonanz).
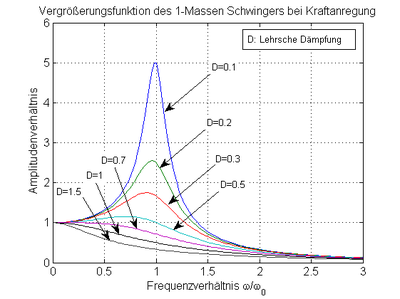
Für D2<0,5 hat die Vergrößerungsfunktion α1 ein Maximum; es liegt bei
 und erreicht den Wert:
und erreicht den Wert: .
.
Bei verschwindender Dämpfung treten im Resonanzfall theoretisch unendlich große Amplituden auf. Auf Grund des Einschwingvorgangs kann sich die Amplitude aber nur linear mit der Zeit aufbauen.[3]
Bei Fliehkraftanregung z. B. durch Unwucht ist die anregende Kraft quadratisch von der Frequenz abhängig. Es ergibt sich die Vergrößerungsfunktion:
- α3 = η2α1
Statt einer Kraftanregung auf die Masse kann das Schwingungssystem auch über das Feder/Dämpferelement angeregt werden. Diese Art der Anregung wird auch als Fußpunktanregung oder Weganregung bezeichnet. Dabei ergibt sich die Vergrößerungsfunktion α4 (siehe Schwingungsisolation, bzw. unten). Beispiel ist das Viertelfahrzeug als einfachstes Modell für das Schwingungsverhalten eines Pkw[4]. Beispiele für die Vergrößerungsfunktionen bei verschiedenen Anregungsarten finden sich in.[5][6][7]
Inhaltsverzeichnis
Herleitung
Kraftanregung
Die Herleitung der Vergrößerungsfunktion bei Kraftanregung erfolgt aus der Differentialgleichung für eine erzwungene Schwingung. Gesucht sei die Amplitude x. Mit Masse m, Federkonstante k und Dämpfungskonstante c folgt:
 .
.
Durch Division mit k:
 .
.
erhält man die Differentialgleichung:
 .
.
Durch Anwendung der Laplace-Transformation erhält man die Übertragungsfunktion:
Mit
 und
und  erhält man den Frequenzgang:
erhält man den Frequenzgang:Den Amplitudenfrequenzgang erhält man als Betrag des komplexen Frequenzgangs:
Als Vergrößerungsfunktion wird der Ausdruck α1(η) bezeichnet:
Bei gegebener Kraftamplitude erhält man die Wegamplitude somit zu:
Weganregung
Der Schwinger wird über das Feder/Dämpferelement mit z(t) angeregt. Diese Form der Anregung wird als Fußpunktanregung bezeichnet. Gesucht sei die Amplitude x. Die Differentialgleichung lautet:
 .
.
Durch Division mit k:
 .
.
erhält man die Differentialgleichung:
 .
.
Durch Anwendung der Laplace-Transformation erhält man die Übertragungsfunktion:
Mit
 und
und  erhält man den Frequenzgang:
erhält man den Frequenzgang:Die Vergrößerungsfunktion erhält man als Betrag des komplexen Frequenzgangs:
Häufig ist nicht die Amplitude des Schwingers von Interesse, sondern dessen Beschleunigung. Mit
erhält man den Amplitudengang:
Der Ausdruck: η2α4 ist die dimensionslose Vergrößerungsfunktion zwischen Weganregung am Fußpunkt und der Beschleunigung.
Siehe auch
Literatur
- Hans Dresig: Maschinendynamik. Springer, Berlin 2007, ISBN 978-3-540-72032-4, S. 526 (Eingeschränkte Vorschau in der Google Buchsuche).
Einzelnachweise
- ↑ Gross, Hauger, Schröder, Wall: Technische Mechanik 3: Kinetik. Springer, ISBN 978-3-642-11264-5.
- ↑ Manfred Mitschke: Dynamik der Kraftfahrzeuge. Band B. Schwingungen. 3. Auflage. Springer-Verlag, 1997, ISBN 3-540-56162-5.
- ↑ K. Magnus, H. H. Müller: Grundlagen der technischen Mechanik. Teubner 1982, ISBN 3-519-02371-7.
- ↑ F. Svaricek: Regelungstechnik. Vorlesungsunterlagen S. 9-12. (online)
- ↑ Uwe Hollburg: Maschinendynamik. 2. Auflage. ISBN 978-3-486-57898-0. (online)
- ↑ Woernle: Technische Mechanik 3. Vorlesungsunterlagen WS 2008/2009. (online)
- ↑ Wandinger: Elastodynamik 2. Vorlesungsunterlagen. (online)
Wikimedia Foundation.