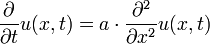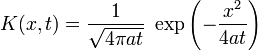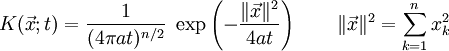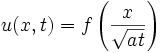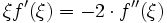Waermeleitungsgleichung

Die Wärmeleitungsgleichung oder Diffusionsgleichung ist eine partielle Differentialgleichung. Sie ist das typische Beispiel einer parabolischen Differentialgleichung. Sie beschreibt die Temperaturverteilung eines Körpers durch Wärmeleitung oder die Ausbreitung eines gelösten Stoffes durch Diffusion.

Die Wärmeleitungsgleichung in einer Raumdimension lautet:

$\frac{\partial}{\partial t} u(x,t)=a\cdot\frac{\partial^2}{\partial x^2} {u(x,t)}$

Hier kann zum Beispiel u(x,t) die Temperatur zur Zeit t an der Stelle x in einem dünnen Stab bezeichnen (wobei a die Temperaturleitfähigkeit ist).

Allgemein in n Dimensionen lautet die Wärmeleitungsgleichung:

$\frac{\partial}{\partial t} u(\vec r,t) =a\cdot\Delta u(\vec{r},t)$,

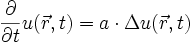wobei Δ der Laplace-Operator ist, also z. B. in 3-dimensionalen kartesischen Koordinaten 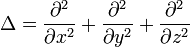$\Delta = \frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}$. Im stationären Fall, wenn also die Zeitableitung Null ist, geht die Gleichung in die Laplace-Gleichung über. (detaillierte Diskussion in der englischen Version).

Lösungen

Die 1-dimensionale Fundamentallösung lautet:

$K(x,t)=\frac{1}{\sqrt{4\pi a t}} \ \exp\left(-\frac{x^2}{4at}\right)$

Eine n-dimensionale Fundamentallösung ist gegeben durch

$K(\vec{x};t)=\frac{1}{(4\pi a t)^{n/2}} \ \exp \left(-\frac{\|\vec{x}\|^2}{4at}\right) \qquad \|\vec{x}\|^2 = \sum_{k=1}^n x_k^2$

K wird auch als „Heat Kernel“ bezeichnet.

Weitere Lösungen

In manchen Fällen kann man Lösungen der Gleichung finden mit Hilfe des Symmetrieansatzes:

$u(x,t) = f\left(\frac{x}{\sqrt{at}}\right)$

Dies führt auf die folgende gewöhnliche Differentialgleichung für f:

$\xi f^\prime(\xi)=-2\cdot f^{\prime\prime}(\xi)$

Eine weitere 1-dimensionale Lösung lautet

$u(x,t) = \sin\left(2 c^2 at - xc\right) \cdot \exp(-cx)$,

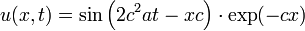wobei c eine Konstante ist. Mit ihr kann man das Wärmespeicherungsverhalten modellieren, wenn ein Gegenstand (mit einer zeitlich sinusförmigen Temperatur) erhitzt wird.

Siehe auch

• Wärme
• Wärmeübertragung
• Wärmekapazität
• Spezifische Wärmekapazität
• Wärmeleitkoeffizient
• Temperaturleitfähigkeit
• Diffusion
• Brownsche Molekularbewegung
• Poröse-Medien-Gleichung