- Widerspruchsfrei
-
In der Logik heißt eine Aussage oder ein Menge von Aussagen widerspruchsfrei oder konsistent, wenn sie keinen Widerspruch enthält und ein solcher auch nicht durch logische Schlussfolgerungen abgeleitet werden kann. Die Widerspruchsfreiheit kann immer nur in Bezug auf einen logischen Kalkül definiert werden und gilt auch nur innerhalb dieses Rahmens. Nicht-konsistente Aussagen werden auch widerspruchsvoll genannt.
Inhaltsverzeichnis
Definition
Man betrachtet einen Kalkül mit einer Ableitbarkeitsrelation
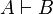 , die als "aus A ist B ableitbar" zu lesen ist. Eine Formelmenge Γ ist genau dann widerspruchsfrei oder konsistent, wenn
, die als "aus A ist B ableitbar" zu lesen ist. Eine Formelmenge Γ ist genau dann widerspruchsfrei oder konsistent, wenn 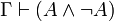 für keine Formel A gilt.
für keine Formel A gilt.Weitere Charakterisierungen
Gilt für die Ableitungsrelation die Regel ex falso quodlibet, dass aus einem Widerspruch jede beliebige Aussage folgt, dann kann die Widerspruchfreiheit alternativ definiert werden:
- In einem Kalkül mit Ableitbarkeitsrelation
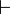 ist eine Formelmenge Γ genau dann widerspruchsfrei, wenn es eine Formel A gibt, für die
ist eine Formelmenge Γ genau dann widerspruchsfrei, wenn es eine Formel A gibt, für die 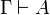 nicht gilt.
nicht gilt.
Die Widerspruchsfreiheit ist auch für einen Kalkül als Ganzes definierbar:
- Ein Kalkül mit Ableitbarkeitsrelation
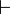 ist genau dann widerspruchsfrei, wenn die leere Formelmenge widerspruchsfrei ist.
ist genau dann widerspruchsfrei, wenn die leere Formelmenge widerspruchsfrei ist.
Relative Konsistenz
Lässt sich aus der Widerspruchsfreiheit einer Formelmenge Γ schon folgern, dass auch die Hinzuname einer Aussage A nicht zu einem Widerspruch führt, so heißt A relativ konsistent zu Γ.
Beispiel
Als Beispiel betrachten wir die folgende Aussagenmenge eines Syllogistik-Kalküls:
{"Alle Griechen sind tapfer.", "Sokrates ist ein Grieche.", "Sokrates ist nicht tapfer."}.
Aus dieser Menge kann die Aussage "Sokrates ist tapfer" sowie die Verneinung dieser Aussage, nämlich "Sokrates ist nicht tapfer", abgeleitet werden. Aus der Menge folgen also widersprüchliche Aussagen, d. h. sie ist nicht widerspruchsfrei oder, wie man auch sagt, sie ist inkonsistent.
Zweck
Das Vorliegen eines Widerspruchs beweist die Falschheit bzw. Ungültigkeit einer Aussage bzw. eines Aussagensystems. Widerspruchsfreiheit ist daher eine wichtige Voraussetzung für
- die Wahrheit von Aussagen, Nachrichten oder Informationen
- die Gültigkeit einer wissenschaftlichen Theorie
- die Brauchbarkeit eines Axiomensystems in der Mathematik
- die Brauchbarkeit eines logischen Kalküls
Widerspruchsfreiheitsbeweise
Das Bedürfnis von Widerspruchsfreiheitsbeweisen trat an der Wende zum 19. Jahrhundert auf, als in der damaligen Mengenlehre Widersprüche bekannt wurden. Schon 1900 thematisierte David Hilbert den Beweis der Widerspruchsfreiheit der Arithmetik im zweiten seiner berühmten mathematischen Probleme. Durch Bertrand Russell, der 1902 in einem Brief an Gottlob Frege auf die die Russellsche Antinomie in dessen Arithmetik-Klassenlogik von 1893 aufmerksam machte, wurde das Problem allgemein bewusst. Er entwarf 1908 die Typentheorie zur Lösung des Problems, die 1910 in die Principia mathematica einging. Sie setzte sich aber wegen ihrer Kompliziertheit nicht dauerhaft durch. Dagegen entwickelte Ernst Zermelo 1907 die axiomatische Mengenlehre, die sich in der Mathematik später durchsetzte in der erweiterten Zermelo-Fraenkel-Mengenlehre. In ihr konnten bisher keine Widersprüche mehr abgeleitet werden, aber auch kein Widerspruchsfreiheitsbeweis erbracht werden. In den Jahren 1920-22 entwickelte dann David Hilbert sein Programm, die Widerspruchsfreiheit axiomatischer Theorien zu beweisen. Es wurde als Hilberts Programm bekannt und konnte für zentrale Teilgebiete der Mathematik und Logik erfolgreich umgesetzt werden, unter anderem von Paul Bernays, Emil Leon Post und John von Neumann, die die Widerspruchsfreiheit der klassischen Aussagenlogik und Prädikatenlogik erster Stufe zeigten. Hilberts Programm, das sich auf finite metalogische Beweismittel beschränkte, versagte aber aufgrund von Kurt Gödels Unvollständigkeitssätzen von 1931 schon bei der Arithmetik. Spätere Mathematiker modifizierten daher Hilberts Programm, indem sie entweder relative Konsistenzbeweise vorlegten (sie zeigen: Ein Zweig der Mathematik ist widerspruchsfrei, sofern ein anderer widerspruchsfrei ist) oder die Beweismittel erweiterten (z.B. um transfinite Methoden). Gerhard Gentzen konnte 1936 mit erweiterten Beweismitteln die Widerspruchsfreiheit der Arithmetik zeigen. Auf seinem Beweis bauten spätere Logiker weitere Widerspruchsfreiheitsbeweise auf, etwa Wilhelm Ackermann 1937 für die allgemeine Mengenlehre mit endlichen (!) Mengen und Paul Lorenzen 1951 für die klassische Analysis.
Siehe auch
Literatur
- Hilbert, David: Mathematische Probleme, 1900, in: Archiv für Mathematik und Physik, 3. Reihe, Band I (1901), 44-63, 213-237.
- Hilbert, David: Neubegründung der Mathematik, 1922, in: Abhandlungen aus dem Mathematischen Seminar der Hamburger Universität, Band I (1922), 157-177.
- Hilbert, David: Die logischen Grundlagen der Mathematik, 1922, in: Mathematische Annalen 88 (1923), 151-165.
- Bernays, Paul: Axiomatische Untersuchung des Aussagenkalkuls der „Principia Mathematica“, Habilitationschrift Göttingen 1918, gekürzt abgedruckt in: Mathematische Zeitschrift 25 (1926), 305-320.
- Post, Emil Leon: Introduction to a General Theory of Elementary Propositions, in: American Journal of Mathematics 43 (1921), 163-185.
- Neumann, John von: Zur Hilbertschen Beweistheorie, in: Mathematische Zeitschrift 26 (1927), 1-46.
- Genzten, Gerhard: Die Widerspruchsfreiheit der reinen Zahlentheorie, in: Mathematische Annalen, 112 (1936), 493-565.
- Gödel, Kurt: Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, Monatshefte für Mathematik und Physik 38 (1931), 173-198.
- Ackermann, Wilhelm: Die Widerspruchsfreiheit der allgemeinen Mengenlehre, mathematische Annalen 114 (1937), 305-315.
- Lorenzen, Paul: Die Widerspruchsfreiheit der klassischen Analysis, in: Mathematische Zeitschrift 54 (1951) 1-24.
- In einem Kalkül mit Ableitbarkeitsrelation
Wikimedia Foundation.
