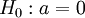Wilcoxon-Rangsummen-Test

Der Wilcoxon-Rangsummentest (nach Frank Wilcoxon (1892–1965)) ist der gebräuchlichste nichtparametrische Test für das Lokationsproblem in der mathematischen Statistik und somit für den Vergleich der Mediane zweier unabhängiger Zufallsgrößen geeignet. Ein äquivalenter Test ist der Mann-Whitney-U-Test.

Erklärung an einem Beispiel

Von zwei Messgeräten gleicher Herstellung ist eines möglicherweise falsch eingestellt. Zur Überprüfung werden mit beiden Geräten einige Messungen gemacht und zwar 10 Messungen X mit dem richtig eingestellten Gerät und 12 Messungen Y mit dem verdächtigen. Wir dürfen unterstellen, dass die Wahrscheinlichkeitsverteilungen von X und von Y bis auf eine Verschiebung gleich sind. Als Nullhypothese nehmen wir an, dass beide Geräte richtig kalibriert sind, also dass die Verschiebung gleich null ist. Als Alternativhypothese nehmen wir einfachshalber an, das andere Gerät weise zu hohe Werte auf. Wir ordnen die Messwerte beider Instrumente nach Größe:

X X X Y X Y X Y Y X Y Y Y X X Y X X Y Y Y Y

Wenn die Nullhypothese richtig ist, hat jede mögliche Anreihung der 10 X-Werte und der 12 Y-Werte die gleiche Wahrscheinlichkeit. Die Wahrscheinlichkeit, dass an einer Stelle ein X steht (und auch die (Gegen-)Wahrscheinlichkeit für ein Y) ist unabhängig davon, ob diese Stelle am Anfang, in der Mitte oder am Ende der Aufreihung ist.

Wenn aber die Alternativhypothese gültig ist, werden die X-Werte sich mehr am Anfang der Reihe konzentrieren und die Y-Werte am Ende. Im Extremfall könnten wir gefunden haben:

X X X X X X X X X X Y Y Y Y Y Y Y Y Y Y Y Y

Dieses Ergebnis legte die Vermutung nahe, dass das verdächtige Gerät tatsächlich zu hoch kalibriert wäre. Finden wir aber:

Y X Y X Y X Y X Y X Y X Y X Y X Y X Y X Y Y

dann ist dies zwar ein merkwürdiges Ergebnis, aber kein Grund, dem verdächtigen Gerät zu misstrauen.

Zu welcher Schlussfolgerung führt nun das gefundene Ergebnis? Auf den ersten Blick scheinen die X-Werte etwas mehr links und die Y-Werte rechts zu liegen. Das wäre ein Indiz gegen die Nullhypothese. Aber ist das Ergebnis signifikant? Dazu berechnen wir als Testgröße W die Gesamtsumme der Ränge der X-Werte in der Anreihung, in unserem Fall also:

W = 1+2+3+5+7+10+14+15+17+18 = 92

Klar ist: je kleiner W ist, desto unglaubhafter wird die Nullhypothese. Das bringt uns auf die Frage: Ist der gefundene Wert W = 92 zu klein, das heißt so klein, dass es Grund gibt, die Nullhypothese abzulehnen? Mit Hilfe der Wahrscheinlichkeitsrechnung kann die Verteilung von W unter der Bedingung der Nullhypothese berechnet werden. Dazu benutzt man die Feststellung, dass die Nullhypothese jeder Anordnung der X- und Y-Werte dieselbe Wahrscheinlichkeit zuweist. Es gibt Tabellen und Computerprogramme für die benötigten Kalkulationen.

Annahmen

Die Zufallsvariablen X und Y haben stetige Verteilungsfunktionen F bzw. G, die sich nur um eine Verschiebung a voneinander unterscheiden, das heißt:

$G(x)=F(x-a)\,$

Es liegen unabhängig Stichproben 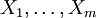$X_1, \dots ,X_m$ von X und 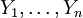$Y_1, \dots ,Y_n$ von Y vor, die auch untereinander unabhängig sind.

Teststatistik

Der Wilcoxon-Rangsummentest für das Testverfahren der Nullhypothese:

$H_0: a=0\,$

hat als Teststatistik:

$W_{m,n} = \sum_{i=1}^m R(X_i)$,

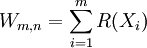wobei R(X_i) der Rang der i-ten X in der gepoolten, geordneten Stichprobe ist. Es werden also nur die Ränge von X aufsummiert. Abhängig von der Alternativhypothese wird die Nullhypothese abgelehnt für zu kleine, zu große oder zu kleine und zu große Werte von W_m,n.

Kritische Werte

Die exakte Verteilung von W_m,n unter der Bedingung der Nullhypothese kann mittels kombinatorischer Überlegungen leicht gefunden werden. Allerdings steigt der Rechenaufwand für große Werte von m,n rasch an. Man kann die exakten kritischen Werte:

P(W_m,n = w) = p_m,n(w)

mittels einer Rekursionsformel berechnen. Die Formel entsteht, wenn man konditioniert auf die Bedingung, ob der letzte Wert in der Anordnung ein X (...X) oder ein Y (...Y) ist.

$p_{m,n}(w)= P(W_{m,n}=w) = P(W_{m,n}=w|...X)P(...X) + P(W_{m,n}=w|...Y)P(...Y)= \,$

$= P(W_{m-1,n}=w-m-n)\frac{m}{m+n} + P(W_{m,n-1}=w)\frac{n}{m+n}=$ :$=\frac{m}{m+n}p_{m-1,n}(w-m-n) + \frac{n}{m+n}p_{m,n-1}(w)$

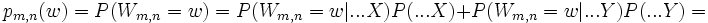
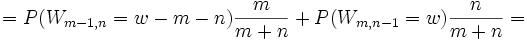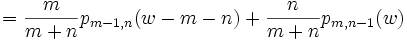
Literatur

• Büning, Trenkler, Nichtparametrische statistische Methoden, de Gruyter, ISBN 3-11-016351-9