Würfelgruppe

Oktaeder

In der Mathematik ist die Oktaedergruppe je nach Konvention

• die Symmetriegruppe eines Oktaeders, also die Menge der Abbildungen, die einen Oktaeder wieder auf sich selbst, d.h. Ecken auf Ecken, Kanten auf Kanten usw. abbilden;
• oder die Drehgruppe eines Oktaeders, eine Untergruppe der Symmetriegruppe, bei der Spiegelungen und Drehspiegelungen nicht zugelassen sind. Die volle Symmetriegruppe wird dann zur Unterscheidung vollständige, binäre oder erweiterte (F. Klein) Oktaedergruppe genannt.

Gemeinsam sind beiden Gruppen die folgenden Abbildungen als Elemente:

• 90°,180°,270°-Drehung um die 3 vierzähligen Drehachsen (durch gegenüber liegende Ecken)
• 120°,240°-Drehung um die 4 dreizähligen Drehachsen (durch gegenüber liegende Flächenmittelpunkte)
• 180°-Drehung um die 6 zweizähligen Drehachsen (durch gegenüber liegende Kantenmittelpunkte)
• die Identität

Daraus ergeben sich 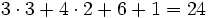$3\cdot3+4\cdot2+6+1=24$ Elemente der Drehgruppe, kombiniert mit Spiegelungen ergeben sich 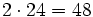$2\cdot24=48$ Elemente der Symmetriegruppe.

Die Gruppen für Oktaeder und Würfel sind kanonisch isomorph, da duale Körper den gleichen Symmetrietyp besitzen. Daher kann man die Oktaedergruppe genauso gut auch Würfelgruppe nennen. Die Drehgruppe des Würfels ist kanonisch isomorph zur symmetrischen Gruppe auf der Menge der Raumdiagonalen, also zur Gruppe der 4! = 24 Permutationen der vier Raumdiagonalen; Drehgruppe von Würfel und Oktaeder sind somit (nicht kanonisch) isomorph zur symmetrischen Gruppe S₄. Die Symmetriegruppe ist das direkte Produkt der Drehgruppe mit der zweielementigen Gruppe, die von der Punktspiegelung am Mittelpunkt erzeugt wird.

In der Kristallographie bezeichnet man die Drehgruppe des Oktaeders mit O und die vollständige Symmetriegruppe mit O_h.