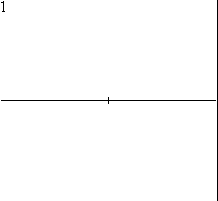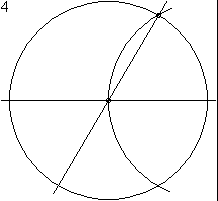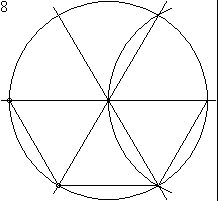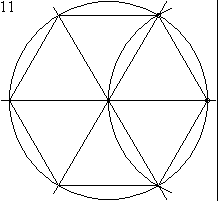Zirkel und Lineal-Geometrie
- Zirkel und Lineal-Geometrie
-
 |
Die Artikel Konstruktion (Mathematik) und Konstruktion mit Zirkel und Lineal überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach vollständiger Abarbeitung der Redundanz. Joriki 15:38, 29. Apr. 2009 (CEST) |
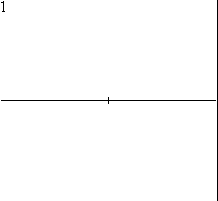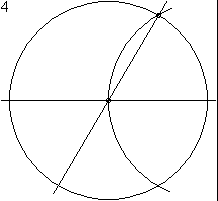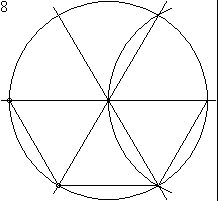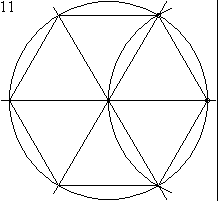
Die Konstruktion eines regelmäßigen Sechsecks nur mit Zirkel und Lineal
Die Konstruktion mit Zirkel und Lineal ist in der Geometrie die klassische Methode, um geometrische Figuren aus vorgegebenen Größen zu zeichnen. Verwendet werden dürfen ausschließlich ein Zirkel und ein Lineal. Letzteres hat keine Markierungen; man kann damit also nur Geraden zeichnen, aber keine Strecken abmessen.
Problemlösungen, die auf andere Hilfsmittel zurückgreifen, wurden von den Griechen der klassischen Periode (und auch später von den meisten Geometrietreibenden bis ins 20. Jahrhundert) als nicht zufriedenstellend betrachtet.
Die Beschränkung auf die „euklidischen Werkzeuge“ leitete sich aus den Postulaten ab, die Euklid am Anfang seines Lehrbuches »Die Elemente« zusammengestellt hatte. Daraus ergeben sich als einzige zugelassene Anwendungen dieser Werkzeuge:
- das Ziehen einer Geraden mit unbeschränkter Länge durch zwei beliebig gegebene, voneinander verschiedene Punkte.
- das Ziehen eines Kreises, der einen beliebig gegebenen Punkt als Mittelpunkt hat und durch einen beliebig gegebenen anderen Punkt verläuft und
- das Übertragen bzw. Abschlagen einer Strecke auf einer Geraden oder einer Kreislinie.
Mit diesen Anwendungen sind folgende algebraische Operationen (also die Konstruktion des Ergebnisses auf dem Zahlenstrahl) möglich:
- die Addition (und Subtraktion) zweier reeller Zahlen;
- die Multiplikation zweier reeller Zahlen;
- das Bestimmen der Inversen einer reellen Zahl (ungleich Null) und damit die Division;
- das Ziehen der Quadratwurzel einer positiven reellen Zahl.
Eine Reihe von geometrischen Problemen konnte jedoch mit diesen Mitteln nicht gelöst werden. Darunter sind die klassischen Probleme der antiken Mathematik:
Der Beweis, dass diese Probleme grundsätzlich nicht mit Zirkel und Lineal zu lösen sind, gelang jedoch erst im 19. Jahrhundert. Dennoch bewirkten die Versuche, das Unmögliche zu vollbringen, eine ganze Reihe von hervorragenden Leistungen. Die Griechen fanden eine Reihe von brillanten Lösungen der »klassischen« Probleme mit anderen Hilfsmitteln, wobei sie viele bemerkenswerte Resultate der höheren Geometrie entdeckten.
Siehe auch
Weblinks
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Zirkel und Lineal — Entwickler René Grothmann Aktuelle Version 9.5 Betriebssystem plattformunabhängig Programmiersprache Java Kategorie … Deutsch Wikipedia
Konstruktion mit Zirkel und Lineal — Die Artikel Konstruktion (Mathematik) und Konstruktion mit Zirkel und Lineal überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen … Deutsch Wikipedia
Zirkel — Zirkelschmied (1568) Der Zirkel ( … Deutsch Wikipedia
Zirkel (Gerät) — Dieser Artikel behandelt das Zeichengerät Zirkel; andere Bedeutungen siehe Zirkel (Begriffsklärung). Zirkel Zirkelschmied (1568) Der Zi … Deutsch Wikipedia
Geometrie — Euklidische Geometrie; Topologie * * * Geo|me|trie [geome tri:], die; : Teilgebiet der Mathematik, das sich mit den räumlichen und nicht räumlichen (ebenen) Gebilden befasst: analytische, projektive Geometrie. * * * Geo|me|trie auch: Geo|met|rie… … Universal-Lexikon
Lineal — Abrichtlineal; Zeichenmaßstab * * * Li|ne|al [line a:l], das; s, e: mit einer Messskala versehenes, langes, schmales, dünnes Gerät aus Holz oder Plastik zum Ziehen gerader Linien: einen Strich mit Bleistift und Lineal zeichnen; die Gartenbeete… … Universal-Lexikon
Geometrie — René Descartes, La Géometrie (Erstausgabe 1637) Die Geometrie (altgriechisch γεωμετρία geometria ‚Erdmaß‘, ‚Landmessung‘) ist ein Teilgebiet der Mathematik. Einerseits versteht man unter Geometrie die zwei und dreidimensionale euklidisch … Deutsch Wikipedia
Kreis (Geometrie) — Leonardo da Vincis: Der vitruvianische Mensch Der Mensch im Mittelpunkt eines Kreises und eines Quadrates. Der Nabel des Menschen ist der Mittelpunkt des Kreises. Der Begriff Kreis gehört zu den wichtigsten Begriffen der euklidischen Geometrie.… … Deutsch Wikipedia
Winkel (Geometrie) — Ein Winkel ist in der Geometrie ein Teil der Ebene, der von zwei in der Ebene liegenden Strahlen (Halbgeraden) mit gemeinsamem Anfangspunkt begrenzt wird. Der gemeinsame Anfangspunkt der beiden Strahlen wird Scheitelpunkt des Winkels,… … Deutsch Wikipedia
Inversion (Geometrie) — Die Inversion, Spiegelung am Kreis oder Kreisspiegelung ist eine spezielle Abbildung der ebenen Geometrie, die das Innere und das Äußere eines gegebenen Kreises miteinander vertauscht. Inhaltsverzeichnis 1 Definition 2 Konstruktion 2.1 Mit Zirkel … Deutsch Wikipedia