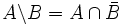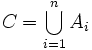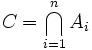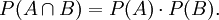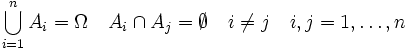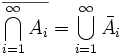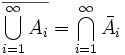- Zufallsereignis
-
Der Begriff Ereignis (auch: Zufallsereignis) bezeichnet in der Wahrscheinlichkeitstheorie eine messbare Menge von Ergebnissen eines Wahrscheinlichkeitsraumes, grob gesprochen also in etwa eine Menge möglicher Ergebnisse eines Zufallsexperiments. Bei einem Würfelwurf entspricht beispielsweise das Ereignis „eine gerade Zahl würfeln“ der Menge {2,4,6}, eine Teilmenge aller möglichen Ergebnisse. Man spricht davon, dass ein Ereignis eintritt, wenn eines seiner Elemente Ausgang eines Zufallsexperiments ist.
Das mit der Ergebnismenge Ω identische Ereignis bezeichnet man als sicheres Ereignis, da es immer eintritt. Im Gegensatz dazu bezeichnet man das mit der leeren Menge identische Ereignis als unmögliches Ereignis. Es tritt nie ein. Beim Beispiel des Würfelwurfs ist das sichere Ereignis die Menge {1,2,3,4,5,6} und das unmögliche Ereignis die Menge
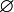 .
.Inhaltsverzeichnis
Gleichheit von Ereignissen
Wenn das Ereignis A das Ereignis B in gleicher Weise nach sich zieht wie das Ereignis B das Ereignis A, dann bezeichnet man die Ereignisse A und B als gleich. A = B
Untermenge
Tritt mit dem Ereignis A stets auch das Ereignis B ein, dann zieht das Ereignis A das Ereignis B nach sich,
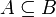 , A bildet eine Untermenge von B.
, A bildet eine Untermenge von B.Ausschließen
Wenn das gleichzeitige Auftreten von zwei Ereignissen A und B unmöglich ist, dann heißt es, die zwei Ereignisse schließen einander aus,
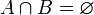 .
.Komplementäres Ereignis
Das zu dem Ereignis A komplementäre Ereignis (Gegenereignis)
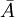 tritt genau dann ein, wenn das Ereignis A nicht eintritt und wird mit
tritt genau dann ein, wenn das Ereignis A nicht eintritt und wird mit 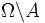 bezeichnet. Speziell gilt:
bezeichnet. Speziell gilt:Summe von Ereignissen
Tritt ein Ereignis C genau dann ein, wenn mindestens eines der Ereignisse A oder B eintritt, dann bezeichnet man das Ereignis C als die Summe der Ereignisse und benutzt dafür die Notation
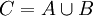 . In Verallgemeinerung auf n Ereignisse schreibt man:
. In Verallgemeinerung auf n Ereignisse schreibt man:Differenz von Ereignissen
Wenn ein Ereignis C nur dann eintritt, wenn ein Ereignis A, aber nicht gleichzeitig das Ereignis B eintritt, dann bezeichnet man das Ereignis C als Differenz der beiden Ereignisse A und B.
Produkt von Ereignissen
Tritt ein Ereignis C genau dann ein, wenn sowohl das Ereignis A als auch das Ereignis B eintritt, dann heißt C das Produkt der Ereignisse mit der Notation
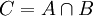 . In Verallgemeinerung auf n Ereignisse schreibt man:
. In Verallgemeinerung auf n Ereignisse schreibt man:Unabhängige Ereignisse
Die zwei Ereignisse A und B heißen voneinander unabhängig, wenn
Unter Verwendung der Formel für die bedingte Wahrscheinlichkeit lässt sich das als
- P(A) = P(A | B)
schreiben, vorausgesetzt P(B) > 0.
Vollständiges System von Ereignissen
Die Ereignisse
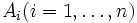 bilden ein vollständiges System von Ereignissen (oder Ereignisssytem), wenn im Ergebnis eines Versuchs genau eines von ihnen eintreten muss.
bilden ein vollständiges System von Ereignissen (oder Ereignisssytem), wenn im Ergebnis eines Versuchs genau eines von ihnen eintreten muss.Beispiel: Die Ereignisse
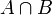 ,
, 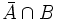 ,
, 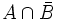 ,
, 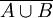 bilden ein solches vollständiges System von Ereignissen.
bilden ein solches vollständiges System von Ereignissen.Formel von de Morgan
Sind
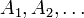 zufällige Ereignisse, dann gelten die de Morganschen Formeln
zufällige Ereignisse, dann gelten die de Morganschen FormelnSiehe auch
Im Artikel Wahrscheinlichkeitstheorie wird der Begriff Ereignis im Kontext mit den anderen Grundbegriffen der Wahrscheinlichkeitstheorie dargestellt.
Literatur
- Rainer Schlittgen: Einführung in die Statistik. 9. Auflage. Oldenbourg Wissenschaftsverlag, Oldenbourg 2000, ISBN 3-486-27446-5
Wikimedia Foundation.