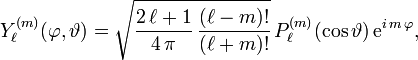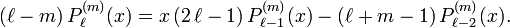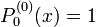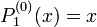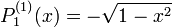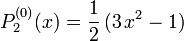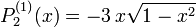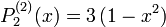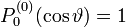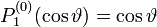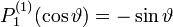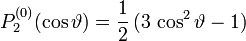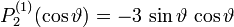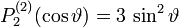Zugeordnete Legendre-Polynome
- Zugeordnete Legendre-Polynome
-
Bei zugeordnete Legendrepolynome bzw. assoziierten Legendrepolynomen, auch zugeordnete Kugelfunktionen genannt, handelt es sich um Funktionen, die in der Mathematik und theoretischen Physik verwendet werden. Da nicht alle zugeordneten Legendrepolynome wirklich Polynome sind, sprechen viele Autoren auch von zugeordneten bzw. assoziierten Legendrefunktionen.
Die zugeordneten Legendrepolynome sind die Lösungen der allgemeinen Legendre-Gleichung: ![(1-x^2) \, \frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} - 2x\frac{\mathrm{d}y}{\mathrm{d}x} + \left(\ell[\ell+1] - \frac{m^2}{1-x^2}\right) \, y = 0](/pictures/dewiki/57/9e52c5cb26f76298b6d304b0b6d73bcd.png)
Diese gewöhnliche Differenzialgleichung hat nicht-singuläre Lösungen im Intervall [-1, 1] nur dann, wenn 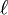 und
und 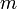 ganzzahlig sind mit
ganzzahlig sind mit 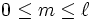 .
.
Man begegnet der allgemeinen Legendre-Gleichung (und damit den zugeordneten Legendrepolynomen) häufig in der Physik, insbesondere wenn eine sphärische Symmetrie vorliegt, wie beispielsweise im Zentralpotential. Hier lassen sich die Laplacegleichung sowie verwandte partielle Differentialgleichungen oft auf die allgemeine Legendre-Gleichung zurückführen. Das prominenteste Beispiel hierfür ist die quantenmechanische Lösung der Energiezustände des Wasserstoffatoms.
Definition
Die zugeordneten Legendrepolynome werden als 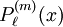 bezeichnet. Am einfachsten lassen sie sich als Ableitungen von gewöhnlichen Legendrepolynomen definieren:
bezeichnet. Am einfachsten lassen sie sich als Ableitungen von gewöhnlichen Legendrepolynomen definieren:
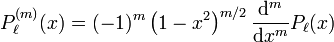
wobei 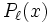 das
das 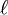 -te Legendrepolynom ist
-te Legendrepolynom ist
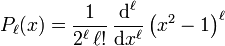 .
.
Daraus ergibt sich
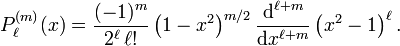
Zusammenhang mit Legendre-Polynomen
Die verallgemeinerte Legendre-Gleichung geht für m = 0 in die Legendre-Gleichung über, sodass  gilt.
gilt.
Orthogonalität
Für die zugeordneten Legendre-Polynome gelten im Intervall I = [-1,1] zwei Orthogonalitätsrelationen:
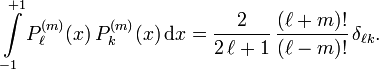
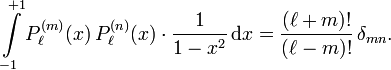
Oft wird 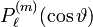 betrachtet, für diese gilt die Normierung auf der Einheitskugel
betrachtet, für diese gilt die Normierung auf der Einheitskugel
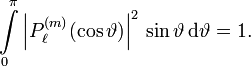
Die zugeordnete Legendre-Gleichung lautet dann
![\frac{\mathrm{d}^2 y}{\mathrm{d} \vartheta^2} + \frac{\cos \vartheta}{\sin \vartheta} \, \frac{\mathrm{d}y}{\mathrm{d} \vartheta} + \left[ \ell\,(\ell+1) - \frac{m^2}{\sin^2 \vartheta} \right] y = 0.](/pictures/dewiki/55/7f4d2d2f28ff7dc7f226acaafee274b2.png)
Über 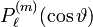 werden die sog. Kugelflächenfunktionen definiert als
werden die sog. Kugelflächenfunktionen definiert als
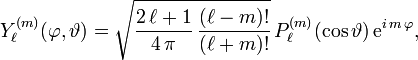
welche auf der Einheitskugel ein vollständiges Orthonormalsystem bilden.
Die ersten zugeordneten Legendre-Polynome
Für die zugeordneten Legendre gilt folgende Rekursionsformel
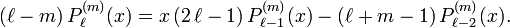
Die ersten Legendre-Polynomen bestimmen sich damit zu
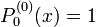
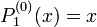
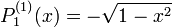
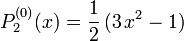
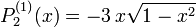
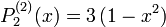
Und mit 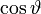 als Argument
als Argument
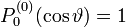
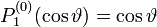
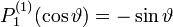
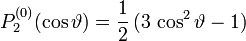
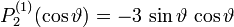
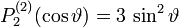
Zugeordnete Legendre Funktionen 2. Art
Ähnlich wie bei der Legendreschen Gleichung stellen die zugeordneten Legendrepolynome 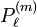 nur eine Gruppe von Lösungsfunktionen der verallgemeinerten Legendreschen Gleichung dar. Die zugeordneten Legendre-Funktionen 2. Art
nur eine Gruppe von Lösungsfunktionen der verallgemeinerten Legendreschen Gleichung dar. Die zugeordneten Legendre-Funktionen 2. Art 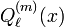 stellen ebenso Lösungen dar. Auch für sie gilt
stellen ebenso Lösungen dar. Auch für sie gilt 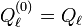 mit den Legendre-Funktionen 2. Art
mit den Legendre-Funktionen 2. Art 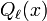 .
.
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Legendre-Polynome — Die Legendre Polynome, auch zonale Kugelfunktionen genannt, sind die partikulären Lösungen der legendreschen Differentialgleichung. Sie sind spezielle reelle oder komplexe Polynome, die ein orthogonales Funktionensystem bilden. Benannt sind sie… … Deutsch Wikipedia
Assoziierte Legendre-Polynome — Bei zugeordnete Legendrepolynome bzw. assoziierten Legendrepolynomen, auch zugeordnete Kugelfunktionen genannt, handelt es sich um Funktionen, die in der Mathematik und theoretischen Physik verwendet werden. Da nicht alle zugeordneten… … Deutsch Wikipedia
Zugeordnete Legendrefunktionen — Bei zugeordnete Legendrepolynome bzw. assoziierten Legendrepolynomen, auch zugeordnete Kugelfunktionen genannt, handelt es sich um Funktionen, die in der Mathematik und theoretischen Physik verwendet werden. Da nicht alle zugeordneten… … Deutsch Wikipedia
Legendre-Polynom — Die Legendre Polynome (nach Adrien Marie Legendre), auch zonale Kugelfunktionen genannt, sind spezielle Polynome, die auf dem Intervall [ 1,1] ein orthogonales Funktionensystem bilden. Sie sind die partikulären Lösungen der legendreschen… … Deutsch Wikipedia
Zugeordnete Legendrepolynome — Bei zugeordneten Legendrepolynomen bzw. assoziierten Legendrepolynomen, auch zugeordnete Kugelfunktionen genannt, handelt es sich um Funktionen, die in der Mathematik und theoretischen Physik verwendet werden. Da nicht alle zugeordneten… … Deutsch Wikipedia
Legendrepolynom — Die Legendre Polynome, auch zonale Kugelfunktionen genannt, sind die partikulären Lösungen der legendreschen Differentialgleichung. Sie sind spezielle reelle oder komplexe Polynome, die ein orthogonales Funktionensystem bilden. Benannt sind sie… … Deutsch Wikipedia
Legendresche Differentialgleichung — Die Legendre Polynome, auch zonale Kugelfunktionen genannt, sind die partikulären Lösungen der legendreschen Differentialgleichung. Sie sind spezielle reelle oder komplexe Polynome, die ein orthogonales Funktionensystem bilden. Benannt sind sie… … Deutsch Wikipedia
Legendresches Polynom — Die Legendre Polynome, auch zonale Kugelfunktionen genannt, sind die partikulären Lösungen der legendreschen Differentialgleichung. Sie sind spezielle reelle oder komplexe Polynome, die ein orthogonales Funktionensystem bilden. Benannt sind sie… … Deutsch Wikipedia
Assoziierte Legendrefunktionen — Bei zugeordnete Legendrepolynome bzw. assoziierten Legendrepolynomen, auch zugeordnete Kugelfunktionen genannt, handelt es sich um Funktionen, die in der Mathematik und theoretischen Physik verwendet werden. Da nicht alle zugeordneten… … Deutsch Wikipedia
Assoziierte Legendrepolynome — Bei zugeordnete Legendrepolynome bzw. assoziierten Legendrepolynomen, auch zugeordnete Kugelfunktionen genannt, handelt es sich um Funktionen, die in der Mathematik und theoretischen Physik verwendet werden. Da nicht alle zugeordneten… … Deutsch Wikipedia
![(1-x^2) \, \frac{\mathrm{d}^2\,y}{\mathrm{d}x^2} - 2x\frac{\mathrm{d}y}{\mathrm{d}x} + \left(\ell[\ell+1] - \frac{m^2}{1-x^2}\right) \, y = 0](/pictures/dewiki/57/9e52c5cb26f76298b6d304b0b6d73bcd.png)
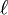 und
und 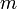 ganzzahlig sind mit
ganzzahlig sind mit 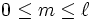 .
.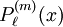 bezeichnet. Am einfachsten lassen sie sich als Ableitungen von gewöhnlichen Legendrepolynomen definieren:
bezeichnet. Am einfachsten lassen sie sich als Ableitungen von gewöhnlichen Legendrepolynomen definieren: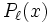 das
das 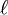 -te Legendrepolynom ist
-te Legendrepolynom ist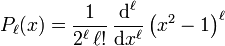 .
.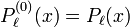 gilt.
gilt.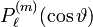 betrachtet, für diese gilt die Normierung auf der Einheitskugel
betrachtet, für diese gilt die Normierung auf der Einheitskugel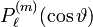 werden die sog. Kugelflächenfunktionen definiert als
werden die sog. Kugelflächenfunktionen definiert als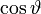 als Argument
als Argument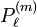 nur eine Gruppe von Lösungsfunktionen der verallgemeinerten Legendreschen Gleichung dar. Die zugeordneten Legendre-Funktionen 2. Art
nur eine Gruppe von Lösungsfunktionen der verallgemeinerten Legendreschen Gleichung dar. Die zugeordneten Legendre-Funktionen 2. Art 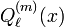 stellen ebenso Lösungen dar. Auch für sie gilt
stellen ebenso Lösungen dar. Auch für sie gilt 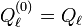 mit den Legendre-Funktionen 2. Art
mit den Legendre-Funktionen 2. Art 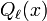 .
.
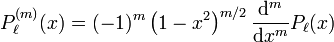
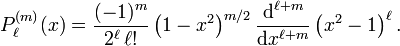
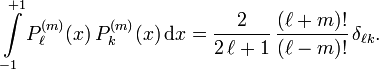
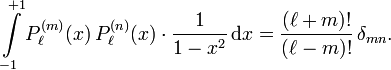
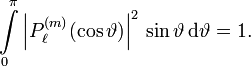
![\frac{\mathrm{d}^2 y}{\mathrm{d} \vartheta^2} + \frac{\cos \vartheta}{\sin \vartheta} \, \frac{\mathrm{d}y}{\mathrm{d} \vartheta} + \left[ \ell\,(\ell+1) - \frac{m^2}{\sin^2 \vartheta} \right] y = 0.](/pictures/dewiki/55/7f4d2d2f28ff7dc7f226acaafee274b2.png)