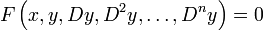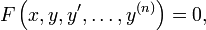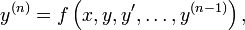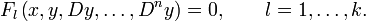Differenzialgleichung

Eine Differentialgleichung, oder auch „Differenzialgleichung“, (oft durch DGL oder DG abgekürzt) ist eine mathematische Gleichung, in der eine gesuchte Funktion y(x), die von einer oder mehreren Variablen abhängt, und Ableitungen dieser Funktion auftreten. Viele Naturgesetze können mittels Differentialgleichungen formuliert werden, bzw. andersherum sind Differentialgleichungen ein wesentliches Werkzeug der mathematischen Modellierung. Ganz allgemein ist

$F\left (x,y,Dy,D^2y, \ldots, D^ny\right ) = 0$

eine Differentialgleichung n-ter Ordnung. Hierbei bezeichnet D^ky die k-ten Ableitungen nach der oder den Unbekannten x. Dabei beschreibt eine Differentialgleichung das Änderungsverhalten dieser Größen zueinander. Differentialgleichungen sind ein wichtiges Objekt der Analysis, die die Lösungstheorie untersucht. Nicht nur weil für viele Differentialgleichungen keine explizite Lösungsdarstellung möglich ist, spielt die näherungsweise Lösung mittels numerischer Verfahren eine wesentliche Rolle.

Auftreten und Anwendungen

Eine Vielzahl von Phänomenen in Natur und Technik kann durch Differentialgleichungen und darauf aufbauende mathematische Modelle beschrieben werden. Einige typische Beispiele sind:

• in der Physik verschiedene Arten von Bewegungen, von Schwingungen oder das Belastungsverhalten von Bauteilen,
• in der Astronomie die Bahnen der Himmelskörper und die Turbulenzen im Innern der Sonne,
• in der Biologie etwa Prozesse bei Wachstum, bei Strömungen oder in Muskeln,
• in der Chemie die Kinetik von Reaktionen,
• in der Elektrotechnik das Verhalten von Netzwerken mit energiespeichernden Elementen,
• in der Differentialgeometrie das Verhalten von Flächen,
• in der Strömungsmechanik das Verhalten eben dieser Strömungen.
• in der Ökonomie die Analyse von wirtschaftlichen Wachstumsprozessen (Wachstumstheorie)

Das Feld der Differentialgleichungen hat der Mathematik entscheidende Impulse verliehen. Viele Teile der aktuellen Mathematik forschen an der Existenz-, Eindeutigkeits- und Stabilitätstheorie verschiedener Typen von Differentialgleichungen.

Typen von Differentialgleichungen

Man unterscheidet verschiedene Typen von Differentialgleichungen. Ganz grob unterteilen sie sich in die folgenden Teilgebiete. Alle der folgenden Typen können im wesentlichen unabhängig und gleichzeitig nebeneinander auftreten.

Gewöhnliche Differentialgleichungen

→ Hauptartikel Gewöhnliche Differentialgleichung

Hängt die Funktion y = y(x) lediglich von einer Variablen 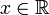$x\in\R$ ab, so spricht man von einer gewöhnlichen Differentialgleichung. Es kommen lediglich gewöhnliche Ableitungen nach der einen Veränderlichen vor.

Schreibt sich die gewöhnliche Differentialgleichung in der Form

$F\left (x,y,y', \ldots, y^{(n)}\right ) = 0,$

so heißt die gewöhnliche Differentialgleichung implizit. Ist die Differentialgleichung nach der höchsten Ableitung aufgelöst, d.h. es gilt

$y^{(n)} = f\left (x,y,y', \ldots, y^{(n-1)}\right ),$

so nennt man die gewöhnliche Differentialgleichung explizit. In den Anwendungen sind explizite gewöhnliche Differentialgleichungen mathematisch einfacher zu verarbeiten. Es gibt eine abgeschlossene Theorie expliziter gewöhnlicher Differentialgleichungen.

Partielle Differentialgleichung

→ Hauptartikel Partielle Differentialgleichung

In diesem Teil ist die Veränderliche x nicht mehr ein Skalar, sondern eine vektorwertige Größe $x=(x_1,\ldots, x_m)\in\mathbb R^m$.

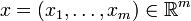Hängt die Lösung y von mehreren Unbekannten 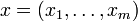$x=(x_1, \ldots, x_m)$ ab und es treten in der Gleichung partielle Ableitungen nach mehr als einer der Unbekannten auf, so spricht man von einer partiellen Differentialgleichung. Partielle Differentialgleichungen sind ein großes Feld und die Theorie ist mathematisch nicht abgeschlossen, sondern Gegenstand der aktuellen Forschung in mehreren Gebieten.

Man unterscheidet verschiedene Typen partieller Differentialgleichungen. Zunächst gibt es lineare partielle Differentialgleichungen. Dabei ist die Funktion F linear in den Größen 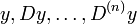$y,Dy, \ldots, D^{(n)}y$. Die Abhängigkeit bezüglich der Variablen x kann durchaus nicht-linear sein. Die Theorie linearer partieller Differentialgleichungen ist am weitesten fortgeschritten, jedoch weit davon entfernt abgeschlossen zu sein.

Hängt die Gleichung sowohl nicht-linear in der Veränderlichen x als auch in der Lösung y ab, so nennt man die partielle Differentialgleichung semi-linear. Eine semi-lineare Gleichung ist schon schwieriger zu behandeln.

Ist nur noch Abhängigkeit von den höchsten Ableitungen linear, so spricht man von einer quasi-linearen partiellen Differentialgleichung. Gerade im Gebiet der quasi-linearen Gleichungen werden zur Zeit die meisten Resultate der aktuellen Forschung ermittelt.

Kann man schließlich auch keine lineare Abhängigkeit bezüglich der höchsten Ableitungen feststellen, nennt man die Gleichung eine nicht-lineare partielle Differentialgleichung oder eine vollständig-nichtlineare partielle Differentialgleichung.

Besonders interessant in dem Gebiet partieller Differentialgleichungen sind die Gleichungen zweiter Ordnung. Das bedeutet, dass Ableitungen bis einschließlich der zweiten Ableitung auftreten. In diesen Spezialfällen gibt es noch weitere Klassifikationsmöglichkeiten.

Weitere Typen

Beim Typus der stochastischen Differentialgleichungen treten in der Gleichung sogenannte stochastische Prozesse auf. Eigentlich sind stochastische Differentialgleichungen keine Differentialgleichungen im obigen Sinne, sondern lediglich gewisse Differentialrelationen, welche als Differentialgleichung interpretiert werden können.

Der Typus der Algebro-Differentialgleichungen zeichnet sich dadurch aus, dass zusätzlich zur Differentialgleichung auch noch algebraische Relationen als Nebenbedingungen gegeben sind.

Weiter gibt es noch sogenannte Delay-Differentialgleichungen. Hier treten neben einer Funktion und ihren Ableitungen an einer Stelle x auch noch Funktionswerte bzw. Ableitungen in der Vergangenheit auf.

Unter einen Integro-Differentialgleichung versteht man eine Gleichung in der nicht nur die Funktion und deren Ableitungen, sondern auch noch Integrationen der Funktion auftauchen.

Je nach Anwendungsgebiet und Methodik gibt es noch weitere Typen von Differentialgleichungen.

Systeme von Differentialgleichungen

Als System von Differentialgleichungen bezeichnet man den Fall, wenn 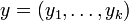$y=(y_1, \ldots, y_k)$ eine vektorwertige Abbildung ist und damit die Gleichung

$F_l \left (x,y,Dy, \ldots, D^{n}y\right ) = 0,\qquad l=1, \ldots, k.$

ebenfalls vektorwertige. Lässt sich dieses implizite Differentialgleichungssystem nicht überall lokal in ein explizites System umwandeln, so handelt es sich um eine Algebro-Differentialgleichung.

Problemstellungen

Die Lösungsmenge einer Differentialgleichung ist im allgemeinen nicht durch die Gleichung selbst eindeutig bestimmt, sondern benötigt zusätzlich noch weitere Anfangs- oder Randwerte. Im Bereich der partiellen Differentialgleichungen können auch sogenannte Anfangsrandwertprobleme auftreten.

Grundsätzlich wird bei Anfangs- oder Anfangsrandwertproblemen eine der Veränderlichen als Zeit interpretiert. Bei diesen Problemen werden gewisse Daten zu einem gewissen Zeitpunkt, nämlich dem Anfangszeitpunkt, vorgeschrieben.

Bei den Randwert- oder Anfangsrandwertproblemen wird eine Lösung der Differentialgleichung in einem beschränkten oder unbeschränktem Gebiet gesucht und wir stellen als Daten sogenannte Randwerte, welche eben auf dem Rand des Gebietes gegeben sind. Je nach Art der Randbedingungen unterscheidet man weitere Typen von Differentialgleichungen, etwa Dirichlet-Probleme oder Neumann-Probleme.

Lösungsmethoden

Auf Grund der Vielfältigkeiten sowohl bei den eigentlichen Differentialgleichungen als auch bei den Problemstellungen ist es nicht möglich, eine allgemein gültige Lösungsmethodik anzugeben. Lediglich explizite gewöhnliche Differentialgleichungen können mit einer geschlossenen Theorie gelöst werden.

Die Fragen der Existenz, Eindeutigkeit, Darstellung und numerischen Berechnung von Lösungen sind somit je nach Gleichung vollständig bis gar nicht gelöst. Aufgrund der Bedeutung von Differentialgleichungen in der Praxis ist hierbei die Anwendung der numerischen Lösungsverfahren besonders bei partiellen Differentialgleichungen der theoretischen Untermauerung voraus.

Eines der Millennium-Probleme ist der Existenzbeweis einer Lösung für sogenannte Navier-Stokes-Gleichungen. Diese Gleichungen treten beispielsweise in der Strömungsmechanik auf.

Beispiele von Differentialgleichungen

• Beispiele von linearen gewöhnlichen Differentialgleichungen
• Beispiele von nichtlinearen gewöhnlichen Differentialgleichungen
• Partielle Differentialgleichungen

Siehe auch

• Integralgleichung

Literatur

• Joseph Petzval: Integration der linearen Differentialgleichungen mit Constanten und veränderlichen Coefficienten. Erster Band. Braumüller, Wien 1853.
• Joseph Petzval: Integration der linearen Differentialgleichungen mit Constanten und veränderlichen Coefficienten. Zweiter Band. Gerold's Sohn, Wien 1859.
• Ludwig Schlesinger: Einführung in die Theorie der Differentialgleichungen mit einer unabhängigen Variabeln. G.J. Göschen, Leipzig 1900.
• Ludwig Schlesinger Vorlesungen über lineare Differentialgleichungen. B. G. Teubner, Leipzig 1908.
• G. H. Golub, J. M. Ortega: Wissenschaftliches Rechnen und Differentialgleichungen. Eine Einführung in die Numerische Mathematik. Heldermann Verlag, Lemgo 1995, ISBN 3-88538-106-0.
• E.L. Ince: Ordinary Differential Equations. Dover Publications, 1956, ISBN 0-486-60349-0.
• G. Oberholz: Differentialgleichungen für technische Berufe - vierte Auflage. Verlag Anita Oberholz, Gelsenkirchen 1995, ISBN 3-9801902-4-2.
• L. Papula: Mathematik für Ingenieure und Naturwissenschaftler Band 2. Viewegs Fachbücher der Technik, Wiesbaden 2001, ISBN 3-528-94237-1.
• J. Sprekels, Bernold Fiedler, Konrad Gröger: International Conference on Differential Equations. World Scientific, 2000, ISBN 981-02-4359-6.

Weblinks

• Matheplanet: Differentialgleichungen – Anleitungen zum Lösen diverser Differentialgleichungen mit Beispielen
• Mathematik-Online Kurs zum Thema Differentialgleichung der Uni Stuttgart
• Prof. Dr. Dörte Haftendorn (Uni Lüneburg) – Differentialgleichungen: Numerik, Beispiele, Isoklinen, ...
• MIT – OpenCourseWare, Differential Equations von Professor Arthur Mattuck