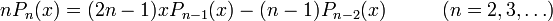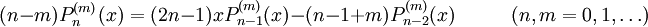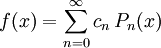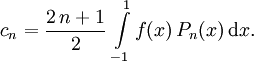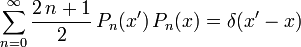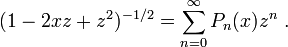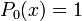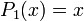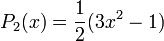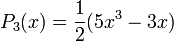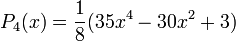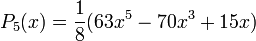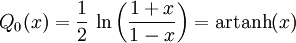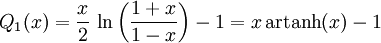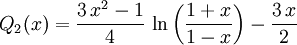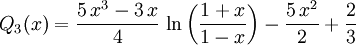- Legendrepolynom
-
Die Legendre-Polynome, auch zonale Kugelfunktionen genannt, sind die partikulären Lösungen der legendreschen Differentialgleichung. Sie sind spezielle reelle oder komplexe Polynome, die ein orthogonales Funktionensystem bilden. Benannt sind sie nach dem Mathematiker Adrien-Marie Legendre. Eine wichtige Rolle spielen die Legendre-Polynome in der theoretischen Physik, insbesondere in der Elektrodynamik und in der Quantenmechanik.
Inhaltsverzeichnis
Herkunft
Konstruktion orthogonaler Polynome
Für ein Intervall I = [a,b] und eine darauf gegebene Gewichtsfunktion
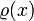 ist eine Folge (Pn) von reellen Polynomen
ist eine Folge (Pn) von reellen Polynomen ![P_n\in\R[X]](/pictures/dewiki/56/8f1dfca941124ba30c555b95041ee1e7.png) orthogonal, wenn sie die Orthogonalitätsbedingung
orthogonal, wenn sie die Orthogonalitätsbedingungfür alle
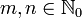 mit
mit 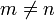 erfüllt. Für das Intervall I = [ − 1,1] zusammen mit der einfachsten aller Gewichtsfunktionen
erfüllt. Für das Intervall I = [ − 1,1] zusammen mit der einfachsten aller Gewichtsfunktionen 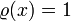 können solche orthogonale Polynome mit Hilfe des Gram-Schmidt'schen Orthogonalisierungsverfahren ausgehend von den Monomen
können solche orthogonale Polynome mit Hilfe des Gram-Schmidt'schen Orthogonalisierungsverfahren ausgehend von den Monomen 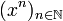 iterativ erzeugt werden. Die Legendre-Polynome ergeben sich, wenn dabei zusätzlich Pn(1) = 1 gefordert wird.
iterativ erzeugt werden. Die Legendre-Polynome ergeben sich, wenn dabei zusätzlich Pn(1) = 1 gefordert wird.Legendresche Differentialgleichung
Die Legendre-Polynome Pn(x) sind Lösungen der legendreschen Differentialgleichung
welche auch in der Form
geschrieben werden kann. Die allgemeine Lösung dieser Differentialgleichung lautet
mit den beiden linear unabhängigen Funktionen Pn(x) und Qn(x). Man bezeichnet die Legendre-Polynome Pn(x) daher auch als Legendre-Funktionen 1. Art und Qn(x) als Legendre-Funktionen 2. Art, denn diese sind keine Polynome mehr.
Legendre-Polynome
Das n-te Legendre-Polynom hat den Grad n und ist aus
![\Bbb Q[x]](/pictures/dewiki/98/b8d87991ade42e2311b8d0bdcf77315b.png) , d.h., es hat rationale Koeffizienten. Für die Legendre-Polynome gibt es mehrere Darstellungsformen bzw. man kann sie rekursiv bestimmen.
, d.h., es hat rationale Koeffizienten. Für die Legendre-Polynome gibt es mehrere Darstellungsformen bzw. man kann sie rekursiv bestimmen.Rodrigues-Formel
Alternative Darstellung
mit
Integraldarstellung
Für alle
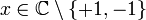 gilt
giltRekursionsformeln
Für die Legendre-Polynome gelten folgende Rekursionsformeln:
Die erste rekursive Formel lässt sich mittels der Substitution n'=n+1 auch wie folgt darstellen:
Durch Anwendung der Ableitungsregel für Ausdrücke der Art y = xn mit y' = nxn − 1 = nx − 1y, bzw. y(m) = (n − m + 1)x − 1y(m − 1) ergibt sich folgende rekursive Darstellung der Legendre-Polynome, welche auch die Ableitungen dieser Polynome berücksichtigt:
Die Anfangsbedingungen lauten
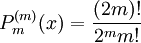 und
und 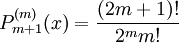 .
.Bei m = 0 ergibt sich wiederum die weiter oben angegebene Formel mit ihren Anfangsbedingungen.
Eigenschaften
Vollständiges Orthogonalsystem
Man betrachte den Hilbert-Raum
![V:= L^2([-1,1]; \R)](/pictures/dewiki/98/beb5290fdc45f68a45a58082a0eca8ac.png) , ausgestattet mit dem Skalarprodukt
, ausgestattet mit dem Skalarprodukt 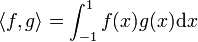 . Die Familie (Pn)n der Legendre-Polynome bildet auf
. Die Familie (Pn)n der Legendre-Polynome bildet auf 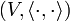 ein vollständiges Orthogonalsystem. Normiert man noch (oder ändert man das Skalarprodukt durch Multiplikation von Konstanten ab), so bilden sie ein vollständiges Orthonormalsystem auf V.
ein vollständiges Orthogonalsystem. Normiert man noch (oder ändert man das Skalarprodukt durch Multiplikation von Konstanten ab), so bilden sie ein vollständiges Orthonormalsystem auf V. 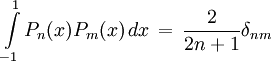 , wobei δnm das Kronecker-Delta bezeichnet. Dabei bedeutet die Vollständigkeit, dass sich jede Funktion
, wobei δnm das Kronecker-Delta bezeichnet. Dabei bedeutet die Vollständigkeit, dass sich jede Funktion 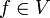 (natürlich im Sinne der von
(natürlich im Sinne der von 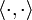 erzeugten Topologie) nach Legendre-Polynomen „entwickeln“ lässt:
erzeugten Topologie) nach Legendre-Polynomen „entwickeln“ lässt:mit den Entwicklungskoeffizienten
In der physikalischen oder technischen Literatur wird die Vollständigkeit gern wie folgt als Distributionsgleichung geschrieben:
wobei δ die diracsche Delta-Distribution ist. Eine solche Distributionsgleichung ist immer so zu lesen, dass beide Seiten dieser Gleichung auf Testfunktionen anzuwenden sind. Wendet man die rechte Seite auf eine solche Testfunktion
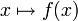 an, so erhält man f(x'). Zur Anwendung der linken Seite muss man definitionsgemäß mit f(x) multiplizieren und anschließend über x integrieren. Dann erhält man aber genau obige Entwicklungsformel (mit x' an Stelle von x). Orthogonalität und Vollständigkeit lassen sich daher kurz und prägnant wie folgt schreiben:
an, so erhält man f(x'). Zur Anwendung der linken Seite muss man definitionsgemäß mit f(x) multiplizieren und anschließend über x integrieren. Dann erhält man aber genau obige Entwicklungsformel (mit x' an Stelle von x). Orthogonalität und Vollständigkeit lassen sich daher kurz und prägnant wie folgt schreiben:- Orthogonalität:
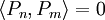 für
für 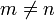 .
. - Vollständigkeit:
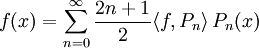 für alle
für alle ![f\in L^2([-1,1]; \R)](/pictures/dewiki/48/025fa481350405c191d808d622ca4ff5.png) (im Sinne der L2-Konvergenz).
(im Sinne der L2-Konvergenz).
Eigenschaften als orthogonales Polynom
Pn(x) hat auf dem Intervall I = [ − 1,1] genau n einfache Nullstellen. Zwischen zwei benachbarten Nullstellen von Pn(x) liegt genau eine Nullstelle von Pn + 1(x).
Allgemeine Eigenschaften
- Pn(1) = 1
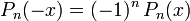
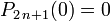
Erzeugende Funktion
Für alle
 ,
, 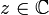 , | z | < 1 gilt
, | z | < 1 giltDabei hat die Potenzreihe auf der rechten Seite für
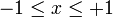 den Konvergenzradius 1.
den Konvergenzradius 1.Die Funktion
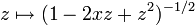 wird daher als erzeugende Funktion der Legendre-Polynome Pn bezeichnet.
wird daher als erzeugende Funktion der Legendre-Polynome Pn bezeichnet.Der in der Physik oft auftretende Term
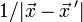 (z. B. in den Potentialen der newtonschen Gravitation oder der Elektrostatik) lässt sich damit in eine Potenzreihe entwickeln für
(z. B. in den Potentialen der newtonschen Gravitation oder der Elektrostatik) lässt sich damit in eine Potenzreihe entwickeln für 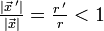 :
:Die ersten Legendre-Polynome
Die ersten Legendre-Polynome auf [ − 1,1] lauten:
Legendre-Funktionen 2. Art
Die Rekursionsformeln der Legendre-Polynome gelten auch für die Legendre-Funktionen 2. Art, so dass diese sich iterativ mit der Angabe der ersten bestimmen lassen:
Siehe auch
Weblinks
- Eric W. Weisstein: Legendre Polynomial auf MathWorld (englisch)
- J. B. Calvert: Legendre Polynomials (englisch)
Wikimedia Foundation.

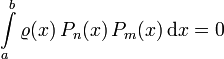
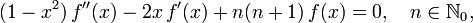
![\frac{\mathrm{d}}{\mathrm{d}x} \left[ (1-x^2) \, f'(x) \right] + n(n+1) \, f(x) = 0](/pictures/dewiki/97/a468304d387a06c5800616a14ba2ced3.png)
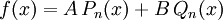
![P_n(x) = \frac{1}{2^n\,n!}\cdot {\mathrm{d}^n \over \mathrm{d}x^n } \left[ (x^2 -1)^n \right]](/pictures/dewiki/51/399ecbf49e375e7ea5af75484d1b59be.png)


![P_n(x) = \frac{1}{\pi} \int_0^\pi \left[x + \sqrt{x^2 - 1} \cos\varphi\right]^n \, \mathrm{d}\varphi](/pictures/dewiki/99/cadaf54ece9d105d1dc287a5b38602c7.png)