Riccati-Differentialgleichung
- Riccati-Differentialgleichung
-
Die riccatische Differentialgleichung ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form
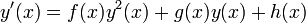 .
.
Sie ist nach dem Mathematiker Jacopo Francesco Riccati benannt, einem italienischen Grafen (1676–1754), der sich intensiv mit der Klassifizierung von Differentialgleichungen befasste und Methoden zur Reduzierung der Ordnung von Gleichungen entwickelte.
Eine allgemeine Integration der Riccati-Differentialgleichung ist mit den üblichen Methoden nicht möglich.
Denselben Namen riccatische Differentialgleichung tragen noch zwei andere Gleichungstypen, die für verschiedene Themen von angewandter Mathematik bis zur Finanzwissenschaft von Bedeutung sind.
Transformation im Falle einer bekannten Lösung
Angenommen, man hätte bereits eine Lösung u (etwa durch Raten) gefunden. Dann lässt sich die riccatische Differentialgleichung vollständig lösen, da das Auffinden der übrigen Lösungen sich nun auf eine bernoullische Differentialgleichung reduziert, welche leicht gelöst werden kann.
Formulierung des Transformationssatzes
Es seien 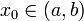 sowie
sowie 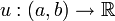 eine Lösung der riccatischen Differentialgleichung
eine Lösung der riccatischen Differentialgleichung
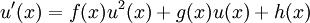
und z eine Lösung der bernoullischen Differentialgleichung
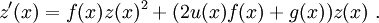
Dann ist
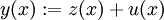
die Lösung der riccatischen Differentialgleichung
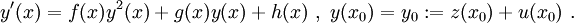
Beweis
Es gilt
![\begin{array}{lll}
y'(x)&=&z'(x) + u'(x)\\
&=&f(x)z(x)^2 + (2u(x)f(x) + g(x))z(x) + f(x)u^2(x) + g(x)u(x) + h(x)\\
&=&f(x)[z(x)^2 + 2u(x)z(x) + u^2(x)] + g(x)[z(x)+u(x)] + h(x)\\
&=&f(x)y^2(x) + g(x)y(x) + h(x)\ ,\\
\end{array}](/pictures/dewiki/48/0a9fa21fa9daf54daf78d1a0392f023a.png)
während der Anfangswert trivialerweise erfüllt ist.
Umformung auf lineare Differentialgleichung zweiter Ordnung
Im Allgemeinen, unabhängig davon, ob man eine spezielle Lösung gefunden hat, lässt sich die riccatische Differentialgleichung auf eine lineare Differentialgleichung zweiter Ordnung mit nicht-konstanten Koeffizienten transformieren. Sollten zufälligerweise die Koeffizienten konstant sein, lässt sich diese transformierte Gleichung mit Hilfe des Verfahrens der Variation der Konstanten leicht vollständig lösen. Im Fall nicht-konstanter Koeffizienten kann auch die lineare Form der riccatischen Differentialgleichung nur sehr schwer lösbar sein.
Formulierung des Transformationssatzes
Es seien 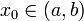 sowie
sowie 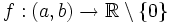 stetig differenzierbar und z eine Lösung der linearen Differentialgleichung zweiter Ordnung
stetig differenzierbar und z eine Lösung der linearen Differentialgleichung zweiter Ordnung
![z''(x) - \left[g(x) + \frac{f'(x)}{f(x)}\right] \cdot z'(x) + [f(x)h(x)] \cdot z(x) = 0](/pictures/dewiki/53/50b2efa9daa927990837182ad6830d2c.png)
mit 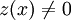 für alle
für alle 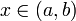 . Dann ist
. Dann ist
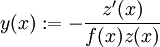
die Lösung der riccatischen Differentialgleichung
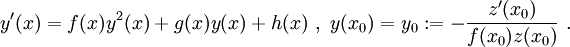
Beweis
Der Übersicht halber werden die Argumente nicht mitgeschrieben. Nach der Quotientenregel gilt
![\begin{array}{lll}
y'&=&\frac{-fzz''+z'(f'z+fz')}{f^2z^2}\\
&=&\frac{-fz[(g+\frac{f'}{f})z' - fhz] + z'(f'z+fz')}{f^2z^2}\\
&=&f\frac{z'^2}{f^2z^2} - g\frac{z'}{fz} + h\\
&=&fy^2 + gy + h\ ,\\
\end{array}](/pictures/dewiki/100/def4c6e2ec56f2668d14d36368bb12b2.png)
während der Anfangswert trivialerweise erfüllt ist.
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Riccati-Gleichung — Die riccatische Differentialgleichung ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form . Sie ist nach dem Mathematiker Jacopo Francesco Riccati benannt, einem italienischen Grafen (1676–1754), der sich intensiv mit… … Deutsch Wikipedia
Riccatische Differentialgleichung — Die riccatische Differentialgleichung ist eine nichtlineare gewöhnliche Differentialgleichung erster Ordnung der Form . Sie ist nach dem Mathematiker Jacopo Francesco Riccati benannt, einem italienischen Grafen (1676–1754), der sich intensiv mit… … Deutsch Wikipedia
Vicenzo Riccati — Vincenzo Riccati Vincenzo Riccati (* 11. Januar 1707 in Castelfranco Veneto, Italien; † 17. Januar 1775 in Treviso) war ein Mathematiker aus dem nördlichen Italien. Er war der zweite Sohn von Jacopo Riccati (1676 1754). Riccati führte unter… … Deutsch Wikipedia
Francesco Siacci — (* 20. April 1839 in Rom; † 31. Mai 1907 in Neapel) war ein italienischer Mathematiker, Ballistiker und Offizier. Francesco Siacci Siacci studierte in Rom und ging nach dem Abschluss 1860 nach Turin, wo er Offizier und Professor für Mechanik an… … Deutsch Wikipedia
Cotangens — Schaubild Tangens Schaubild Kotangens Tangens und Kotangens sind trigonometrische Funktionen und spielen in der Mathematik und ihren Anwendungsgebieten eine herausragende Rolle. Der Tangens des Winkels … Deutsch Wikipedia
Kotangens — Schaubild Tangens Schaubild Kotangens Tangens und Kotangens sind trigonometrische Funktionen und spielen in der Mathematik und ihren Anwendungsgebieten eine herausragende Rolle. Der Tangens des Winkels … Deutsch Wikipedia
Kotangensfunktion — Schaubild Tangens Schaubild Kotangens Tangens und Kotangens sind trigonometrische Funktionen und spielen in der Mathematik und ihren Anwendungsgebieten eine herausragende Rolle. Der Tangens des Winkels … Deutsch Wikipedia
Regelungstheorie — Die Regelungsheorie (auch Kontrolltheorie genannt) ist ein Teilgebiet der angewandten Mathematik. Sie betrachtet dynamische Systeme, deren Verhalten durch sogenannte Eingangsgrößen von außen beeinflusst werden kann. Beispiele für Systeme sind in… … Deutsch Wikipedia
Tangens — Schaubild Tangens Schaubild Kotangens Tangens und Kotangens sind trigonometrische Funktionen und spielen in der Mathematik und ihren Anwendungsgebieten eine herausragende Rolle. Der Tangens des Winkels … Deutsch Wikipedia
Tangensfunktion — Schaubild Tangens Schaubild Kotangens Tangens und Kotangens sind trigonometrische Funktionen und spielen in der Mathematik und ihren Anwendungsgebieten eine herausragende Rolle. Der Tangens des Winkels … Deutsch Wikipedia
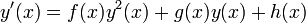 .
.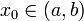 sowie
sowie 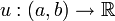 eine Lösung der riccatischen Differentialgleichung
eine Lösung der riccatischen Differentialgleichung
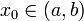 sowie
sowie 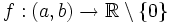 stetig differenzierbar und z eine Lösung der linearen Differentialgleichung zweiter Ordnung
stetig differenzierbar und z eine Lösung der linearen Differentialgleichung zweiter Ordnung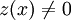 für alle
für alle 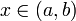 . Dann ist
. Dann ist

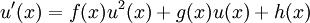
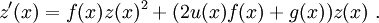
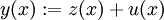
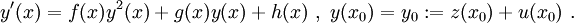
![\begin{array}{lll}
y'(x)&=&z'(x) + u'(x)\\
&=&f(x)z(x)^2 + (2u(x)f(x) + g(x))z(x) + f(x)u^2(x) + g(x)u(x) + h(x)\\
&=&f(x)[z(x)^2 + 2u(x)z(x) + u^2(x)] + g(x)[z(x)+u(x)] + h(x)\\
&=&f(x)y^2(x) + g(x)y(x) + h(x)\ ,\\
\end{array}](/pictures/dewiki/48/0a9fa21fa9daf54daf78d1a0392f023a.png)
![z''(x) - \left[g(x) + \frac{f'(x)}{f(x)}\right] \cdot z'(x) + [f(x)h(x)] \cdot z(x) = 0](/pictures/dewiki/53/50b2efa9daa927990837182ad6830d2c.png)
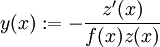
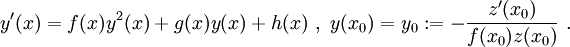
![\begin{array}{lll}
y'&=&\frac{-fzz''+z'(f'z+fz')}{f^2z^2}\\
&=&\frac{-fz[(g+\frac{f'}{f})z' - fhz] + z'(f'z+fz')}{f^2z^2}\\
&=&f\frac{z'^2}{f^2z^2} - g\frac{z'}{fz} + h\\
&=&fy^2 + gy + h\ ,\\
\end{array}](/pictures/dewiki/100/def4c6e2ec56f2668d14d36368bb12b2.png)