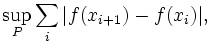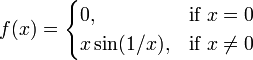- Beschränkte Schwankung
-
In der Analysis ist eine Funktion f von beschränkter Variation (beschränkter Schwankung), wenn ihre totale Variation (totale Schwankung) endlich ist, sie also in gewisser Weise nicht beliebig stark oszilliert. Diese Begriffe hängen eng mit der Stetigkeit und der Integrierbarkeit von Funktionen zusammen.
Der Raum aller Funktionen von beschränkter Variation auf dem Gebiet Ω wird mit BV(Ω) bezeichnet.
Inhaltsverzeichnis
Reelle Funktionen
Die totale Variation einer reellwertigen Funktion f:
![[a, b]\rightarrow \mathbb{R}](/pictures/dewiki/52/4383dae020756de02c1047284ebd3679.png) , die auf einem abgeschlossenen Intervall definiert ist, ist das Supremum
, die auf einem abgeschlossenen Intervall definiert ist, ist das Supremumwobei dieses Supremum über alle möglichen Partitionen P = { x1, ..., xn } des Intervalls [a, b] gebildet wird.
Genau die stetigen Funktionen von beschränkter Variation sind Riemann-Stieltjes-integrierbar. Deshalb kann BV[a, b] mit einer Seminorm ausgestattet werden:
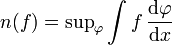 .
.
Dieses Supremum wird über alle Funktionen
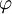 mit kompaktem Träger und Funktionswerten im Intervall [-1,1] gebildet.
mit kompaktem Träger und Funktionswerten im Intervall [-1,1] gebildet.Die Seminorm stimmt mit dem Supremum, das die beschränkte Variation definiert, überein.
Beispiel
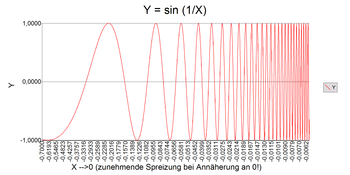
Ein einfaches Beispiel für eine unbeschränkte Variation ist die Funktion y=sin(1/x) in der Nähe von x=0. Es ist anschaulich einsichtig, das der Wert des Quotienten (1/x) für x -> 0 mit zunehmender Annäherung an 0 immer schneller gegen ∞ anwachsen wird, und damit der Sinus dieses Werts dabei unendlich viele Schwingungen durchlaufen wird. Dies zeigt das Bild rechts.
Die Funktion
ist ebenfalls nicht von beschränkter Schwankung im Intervall [a, b], im Gegensatz zur Funktion:
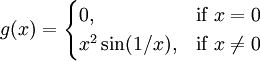 .
.
Hier wird die Variation des Sinusterms, die für
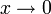 stark zunimmt, durch die zusätzliche Potenz genug gedämpft.
stark zunimmt, durch die zusätzliche Potenz genug gedämpft.Mehrdimensionale Funktionen
Im mehrdimensionalen Fall wird der Begriff der totalen Variation über die schwache Ableitung definiert.
Zusammenhang zu rektifzierbaren Wegen
Eine Funktion f:
![[a, b]\rightarrow \mathbb{R}](/pictures/dewiki/52/4383dae020756de02c1047284ebd3679.png) kann auch als Weg im metrischen Raum
kann auch als Weg im metrischen Raum  aufgefasst werden. Es gilt, dass f genau dann von beschränkter Variation ist wenn f ein rektifizierbarer Weg ist, also eine endliche Länge hat.
aufgefasst werden. Es gilt, dass f genau dann von beschränkter Variation ist wenn f ein rektifizierbarer Weg ist, also eine endliche Länge hat.
Wikimedia Foundation.