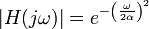Binomialfilter

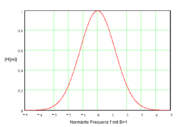
Betragsfrequenzgang von H(jω) eines Gauß-Filters mit normierter Frequenz und einer Bandbreite B von 1.

Impulsantwort h(t) eines Gauß-Filters

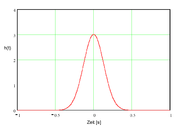
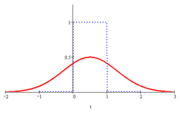
Gauß-Filter sind Frequenzfilter, welche bei der Sprungantwort keine Überschwingung aufweisen und gleichzeitig maximale Flankensteilheit im Übergangsbereich aufweisen. Als Besonderheit besitzt bei diesem Filter sowohl die Übertragungsfunktion als auch die Impulsantwort den Verlauf einer gaußschen Glockenkurve, wie in den Abbildungen rechts dargestellt, wovon sich auch der Name dieses Filtertyps ableitet.

Anwendungsbereiche dieses Filters liegen bei digitalen Modulationsverfahren und im Bereich der Bildverarbeitung.

Übertragungsfunktion

Der Betrag der Übertragungsfunktion H(jω) ist bei Gauß-Filtern gegeben durch

$|H(j\omega)| = e^{- \left( {\frac{\omega}{2 \alpha}} \right) ^2}$

mit der Konstanten α

$\alpha = \frac{\pi}{\sqrt{\ln(\sqrt{2})}}$.

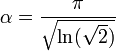Die Impulsantwort eines Gauß-Filters lautet

$h(t) = \frac{\alpha}{\sqrt{\pi}} e^{{-(\alpha t)}^2}$.

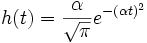Anwendungen

Digitale Signalverarbeitung

Ein Rechteckimpuls, blau punktiert dargestellt, wird durch die Impulsformung eines Gauß-Filters in den rot dargestellten Signalverlauf übergeführt.

Gauß-Filter besitzen eine konstante, minimale Gruppenlaufzeit im Sperr- und Durchlassbereich. Dies erlaubt den Einsatz dieses Filter primär zur Impulsformung mit Anwendungsbereichen in der digitalen Signalverarbeitung.

Die Impulsformung findet sich bei digitalen Modulationsverfahren wie dem Gaussian Frequency Shift Keying (GMSK), da damit die einzelnen, meist rechteckförmigen Sendesymbole in Impulse der gaußschen Glockenkurve mit geringeren Bandbreitenbedarf als die ursprünglichen rechteckförmigen Sendesymbole umgewandelt werden können. Damit ist eine höhere spektrale Effizienz des Modulationsverfahrens verbunden.

In Mobilfunksystemen, wie dem GSM, werden Gauß-Filter im Rahmen der GMSK-Modulation auf der Funkschnittstelle zur Übertragung der digitalen Sprach- und Steuerinformationen eingesetzt.

Bildverarbeitung

In der Bildverarbeitung werden Gauß-Filter zur Glättung oder „Weichzeichnen“ des Bildinhaltes verwendet. Es kann damit das Bildrauschen vermindert werden: Kleinere Strukturen gehen verloren, grobere Strukturen bleiben dagegen erhalten. Spektral kommt die Glättung einem Tiefpassfilter gleich.

Da ein Bild zwei Dimensionen aufweist, muss für die Bildverarbeitung die Impulsantwort auf zwei Dimensionen erweitert werden. Die Impulsantwort besitzt zwei Argumente x und y für jede Raumrichtung:

$h(x,y) = \frac{\alpha}{\sqrt{\pi}} e^{- \alpha^2 (x^2 + y^2)}$.

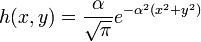Für praktische Realisierungen im Rahmen der digitalen Bildverarbeitung wird die diskrete Impulsantwort meist in Form einer zweidimensionalen Matrix verwendet.

Alternativ wird in der Literatur bei der Beschreibung von Gauß-Filtern statt der Konstanten α dazu gleichwertig die Varianz σ² in dem Ausdruck der Impulsantwort verwendet − was das mathematische Naheverhältnis der Impulsantwort eines Gauß-Filters zu der Funktion der zweidimensionalen Normalverteilung ausdrückt:

$h(x,y) = \frac{1}{\sqrt{\sigma^2{2\pi}}}e^{-\frac{x^2+y^2}{2\sigma^2}}$.

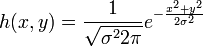Literatur

• Karl Dirk Kammeyer, Volker Kühn: MATLAB in der Nachrichtentechnik. 1 Auflage. J. Schlembach Fachverlag, 2001, ISBN 3-935340-05-2.