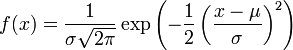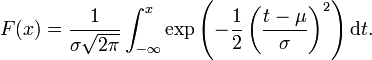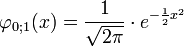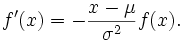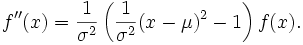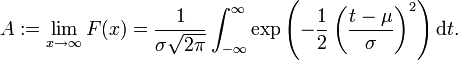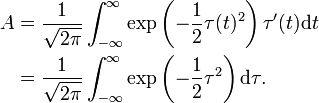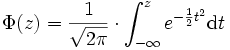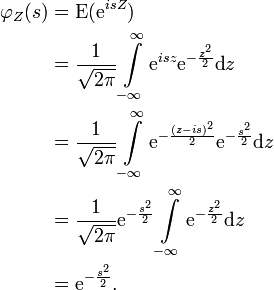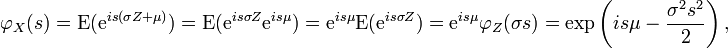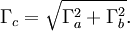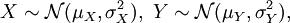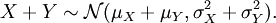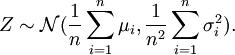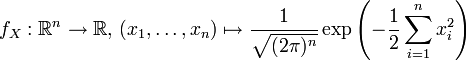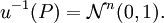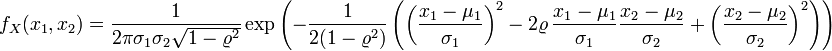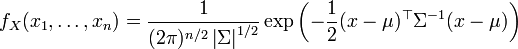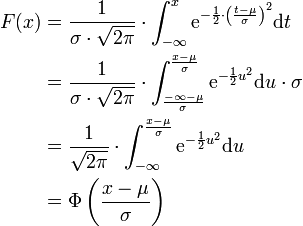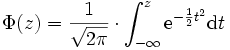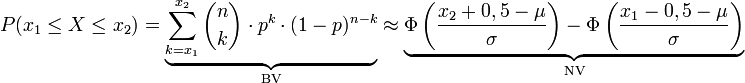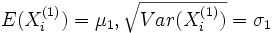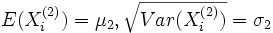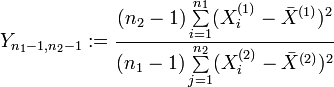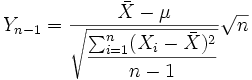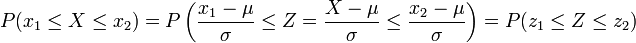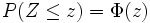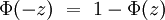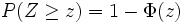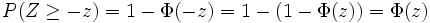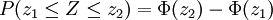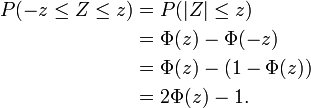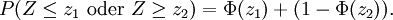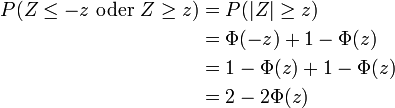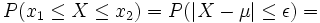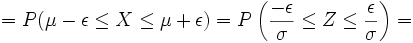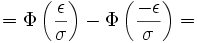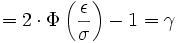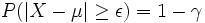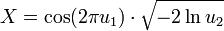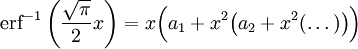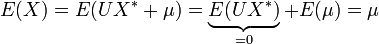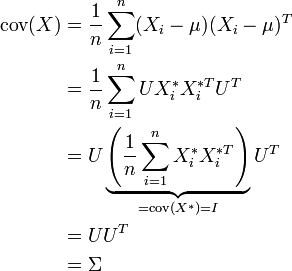Gaußsche Glockenkurve

Dichten normalverteilter Zufallsgrößen

Die Normal- oder Gauß-Verteilung (nach Carl Friedrich Gauß) ist ein wichtiger Typ kontinuierlicher Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichte wird auch Gauß-Funktion, Gauß-Kurve, Gauß-Glocke oder Glockenkurve genannt.

Die besondere Bedeutung der Normalverteilung beruht unter anderem auf dem zentralen Grenzwertsatz, der besagt, dass eine Summe von n unabhängigen, identisch verteilten Zufallsvariablen im Grenzwert 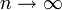$n\rightarrow\infty$ normalverteilt ist. Das bedeutet, dass man Zufallsvariablen dann als normalverteilt ansehen kann, wenn sie durch Überlagerung einer großen Zahl von unabhängigen Einflüssen entstehen, wobei jede einzelne Einflussgröße einen im Verhältnis zur Gesamtsumme unbedeutenden Beitrag liefert.

Viele natur-, wirtschafts- und ingenieurswissenschaftliche Vorgänge lassen sich durch die Normalverteilung entweder exakt oder wenigstens in sehr guter Näherung beschreiben (vor allem Prozesse, die in mehreren Faktoren unabhängig voneinander in verschiedene Richtungen wirken).

Zufallsgrößen mit Normalverteilung benutzt man zur Beschreibung zufälliger Vorgänge wie:

• zufällige Messfehler,
• zufällige Abweichungen vom Nennmaß bei der Fertigung von Werkstücken,
• Beschreibung der brownschen Molekularbewegung.

In der Versicherungsmathematik ist die Normalverteilung geeignet zur Modellierung von Schadensdaten im Bereich mittlerer Schadenshöhen.

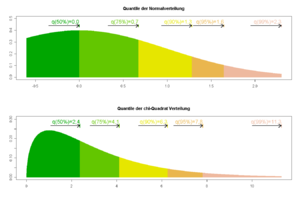
In der Messtechnik wird häufig eine Normalverteilung angesetzt, die die Streuung der Messfehler beschreibt. Hierbei ist von Bedeutung, wie viele Messpunkte innerhalb einer gewissen Streubreite liegen. Die Standardabweichung σ beschreibt die Breite der Normalverteilung. Berücksichtigt man die tabellierten Werte der Verteilungsfunktion, gilt näherungsweise folgende Aussage:

• 68,27 % aller Messwerte haben eine Abweichung von höchstens σ vom Mittelwert,
• 95,45 % aller Messwerte haben eine Abweichung von höchstens 2σ vom Mittelwert,
• 99,73 % aller Messwerte haben eine Abweichung von höchstens 3σ vom Mittelwert.

Somit kann neben dem Mittelwert auch der Standardabweichung eine physikalische Bedeutung zugeordnet werden.

Definition

Eine stetige Zufallsvariable X mit der Wahrscheinlichkeitsdichte $f:\R\to\R_{>0},\ x\mapsto f(x)$

$f(x) = \frac {1}{\sigma\sqrt{2\pi}}\exp\left(-\frac {1}{2} \left(\frac{x-\mu}{\sigma}\right)^2\right)$ ^[1]

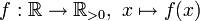
heißt μ-σ-normalverteilt, auch geschrieben als 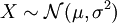$X \sim \mathcal N(\mu, \sigma^2)$ oder (μ,σ²)-normalverteilt, wobei μ der Erwartungswert und σ die Standardabweichung sind.

Die Verteilungsfunktion der Normalverteilung ist gegeben durch

$F(x) = \frac{1}{\sigma\sqrt{2\pi}} \int_{-\infty}^x \exp\left(-\frac{1}{2} \left(\frac{t-\mu}{\sigma}\right)^2\right) \mathrm dt.$

Dichtefunktion der Standardnormalverteilung $\varphi_{0;1}(x)=\frac {1}{\sqrt{2\pi}} \cdot e^{-\frac {1}{2} x^2}$

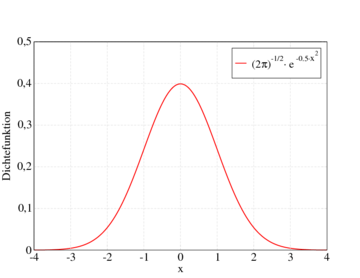
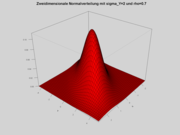
So sieht die Dichtefunktion der Standardnormalverteilung (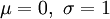$\mu=0,\ \sigma = 1$) aus. Angegeben sind die Intervalle im Abstand 1, 2 und 3 Standardabweichungen vom Erwartungswert 0, die rund 68 %, 95,5 % und 99,7 % der Fläche unter der Glockenkurve umfassen. Die gleichen Prozentsätze gelten für alle Normalverteilungen in Bezug auf die entsprechenden Erwartungswerte und Standardabweichungen. Man beachte, dass die Dichte der Normalverteilung nie den Wert Null annimmt, das heißt es gilt f(x) > 0 für alle reellen x.

Die Normalverteilung ist eine Grenzverteilung, die nicht direkt beobachtet werden kann. Die Annäherung verläuft aber mit wachsendem n sehr schnell, so dass schon die Verteilung einer Summe von 30 oder 40 unabhängigen, identisch verteilten Zufallsgrößen einer Normalverteilung recht ähnlich ist.

Eigenschaften

Symmetrie

Der Graph der Wahrscheinlichkeitsdichte 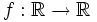$f:\R\to\R$ ist eine Gauß'sche Glockenkurve, deren Höhe und Breite von σ abhängt. Sie ist achsensymmetrisch zur Achse x = μ. Ihre Stammfunktion F ist Punktsymmetrisch zu P(μ | 0,5).

Maximalwert und Wendepunkte der Dichtefunktion

Mit Hilfe der ersten und zweiten Ableitung lassen sich der Maximalwert und die Wendepunkte bestimmen. Die erste Ableitung ist

$f'(x) = -\frac{x-\mu}{\sigma^2} f(x).$

Das Maximum der Dichtefunktion der Normalverteilung liegt demnach bei x_max = μ und beträgt dort $f_\mathrm{max} = \frac 1{\sigma\sqrt{2\pi}}.$

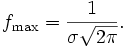
Die zweite Ableitung lautet

$f''(x) = \frac 1{\sigma^2}\left(\frac 1{\sigma^2}(x-\mu)^2-1\right) f(x).$

Somit liegen die Wendepunkte der Dichtefunktion bei $x=\mu\pm\sigma$.

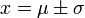Normierung

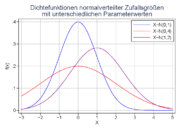
Wichtig ist, dass die gesamte Fläche unter der Kurve gleich 1 ist, also der Wahrscheinlichkeit eines sicheren Ereignisses entspricht. Somit folgt, dass, wenn zwei gaußsche Glockenkurven dasselbe μ, aber unterschiedliche σ-Werte haben, jene Kurve mit dem größeren σ breiter und niedriger ist (da ja beide zugehörigen Flächen jeweils den Wert von 1 haben und nur die Standardabweichung (oder „Streuung“) höher ist). Zwei Glockenkurven mit dem gleichen σ, aber unterschiedlichen μ haben gleich aussehende Graphen, die jedoch auf der x-Achse um die Differenz der μ-Werte zueinander verschoben sind.

Die Normierung lässt sich wie folgt nachweisen:

Wir definieren

$A := \lim_{x \to \infty} F(x) = \frac 1{\sigma \sqrt{2\pi}} \int_{-\infty}^\infty \exp\left(-\frac 12 \left(\frac{t-\mu}\sigma\right)^2\right) \mathrm dt.$

Ist die Verteilung F normiert, so muss A = 1 gelten.

Um das Integral zu vereinfachen, verwenden wir die lineare Substitution 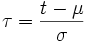$\tau = \frac{t-\mu}\sigma$ und erhalten dann wegen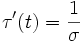 $\tau'(t) = \frac 1\sigma$

$\begin{align} A &= \frac 1{\sqrt{2\pi}} \int_{-\infty}^\infty \exp\left(-\frac 12 \tau(t)^2\right) \tau'(t) \mathrm dt\\ &= \frac 1{\sqrt{2\pi}} \int_{-\infty}^\infty \exp\left(-\frac 12 \tau^2\right) \mathrm d\tau. \end{align}$

Wie erwartet ist A unabhängig von den Parametern σ und μ. Für die Normiertheit dieses Integrals siehe den Artikel Fehlerintegral.

Berechnung

Da sich das Integral der Wahrscheinlichkeitsdichtefunktion nicht auf eine elementare Stammfunktion zurückführen lässt, wurde für die Berechnung früher meist auf Tabellen zurückgegriffen (siehe dazu die Tabelle der Verteilungsfunktion der Standardnormalverteilung); heutzutage sind entsprechende Zellenfunktionen in üblichen Tabellenkalkulationsprogrammen stets verfügbar. Tabellen wie Zellenfunktionen gelten aber in der Regel nicht für beliebige μ- und σ-Werte, sondern nur für die Standardnormalverteilung, bei der μ = 0 und σ = 1 ist (man spricht auch von einer 0-1-Normalverteilung oder normierten Normalverteilung).

Die Tabellen sind also für die Wahrscheinlichkeitsverteilungsfunktion Φ (auch Gauß'sches Fehlerintegral genannt) mit

$\Phi(z)=\frac 1{\sqrt{2\pi}} \cdot \int_{-\infty}^z e^{-\frac 12 t^2} \mathrm{d}t$

ausgelegt. Analog dazu wird die zugehörige normierte Wahrscheinlichkeitsdichtefunktion f mit φ bezeichnet.

Ist nun eine beliebige μ-σ-Verteilung gegeben, so muss diese nur in eine Standardnormalverteilung transformiert werden.

Erwartungswert

Die Normalverteilung besitzt den Erwartungswert

$\operatorname{E}(X) =\frac{1}{\sigma\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty}x \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\operatorname{d}x = \mu$.

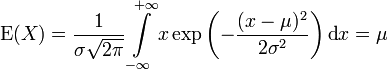Varianz und Standardabweichung

Die Varianz ergibt sich analog zu

$\operatorname{Var}(X) = \frac{1}{\sigma\sqrt{2\pi}}\int\limits_{-\infty}^{+\infty}(x-\mu)^2 \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\operatorname{d}x = \sigma^2$.

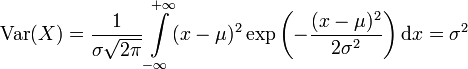Für die Standardabweichung ergibt sich

$\sqrt{\operatorname{Var}(X)} = \sigma$.

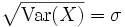Variationskoeffizient

Aus Erwartungswert und Standardabweichung erhält man unmittelbar den Variationskoeffizienten

$\operatorname{VarK}(X) = \frac{\sigma}{\mu}$.

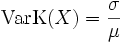Schiefe

Die Schiefe besitzt unabhängig von den Parametern μ und σ immer den Wert 0.

Charakteristische Funktion

Die charakteristische Funktion für eine standardnormalverteilte Zufallsvariable 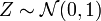$Z \sim \mathcal N(0,1)$ berechnet sich gemäß

$\begin{align} \varphi_Z(s) &= \operatorname E(\mathrm e^{isZ})\\ &= \frac 1{\sqrt{2\pi}}\int\limits_{-\infty}^\infty \mathrm e^{isz} \mathrm e^{-\frac{z^2}2} \operatorname dz\\ &= \frac 1{\sqrt{2\pi}}\int\limits_{-\infty}^\infty \mathrm e^{-\frac{(z-is)^2}2} \mathrm e^{-\frac{s^2}2} \operatorname dz\\ &= \frac 1{\sqrt{2\pi}}\mathrm e^{-\frac{s^2}2} \int\limits_{-\infty}^\infty \mathrm e^{-\frac{z^2}2} \operatorname dz\\ &= \mathrm e^{-\frac{s^2}2}. \end{align}$

Den Übergang von der dritten zur vierten Zeile erhält man dabei durch Anwendung des Cauchyschen Integralsatzes.

Für eine Zufallsvariable 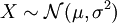$X \sim \mathcal N(\mu, \sigma^2)$ erhält man nun

$\varphi_X(s) = \operatorname E(\mathrm e^{is(\sigma Z + \mu)}) = \operatorname E(\mathrm e^{is\sigma Z}\mathrm e^{is\mu}) = \mathrm e^{is\mu}\operatorname E(\mathrm e^{is\sigma Z}) = \mathrm e^{is\mu}\varphi_Z(\sigma s) = \exp\left(is\mu-\frac{\sigma^2 s^2}2\right),$

wobei $Z \sim \mathcal N(0,1)$.

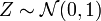Momenterzeugende Funktion

Die momenterzeugende Funktion der Normalverteilung ist

$m_X(s) = \exp\left(\mu s+\frac{\sigma^2 s^2}2\right)$.

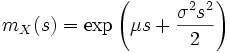Momente

Sei X N(μ,σ²)-verteilt. Dann sind die ersten Momente wie folgt:

Nummer, k	Moment, E(X^k)	zentriertes Moment	Kumulante
0	1	1
1	μ	0	μ
2	μ2 + σ2	σ2	σ2
3	μ3 + 3μσ2	0	0
4	μ4 + 6μ2σ2 + 3σ4	3σ4	0
5	μ5 + 10μ3σ2 + 15μσ4	0	0
6	μ6 + 15μ4σ2 + 45μ2σ4 + 15σ6	15σ6	0
7	μ7 + 21μ5σ2 + 105μ3σ4 + 105μσ6	0	0
8	μ8 + 28μ6σ2 + 210μ4σ4 + 420μ2σ6 + 105σ8	105σ8	0

Invarianz gegenüber Faltung

Die Normalverteilung ist invariant gegenüber der Faltung, d. h. die Summe unabhängiger normalverteilter Zufallsgrößen ist wieder normalverteilt. Eine veranschaulichende Formulierung dieses Sachverhaltes lautet: Die Faltung einer Gaußkurve der Halbwertsbreite Γ_a mit einer Gaußkurve der Halbwertsbreite Γ_b ergibt wieder eine Gaußkurve mit der Halbwertsbreite

$\Gamma_c = \sqrt{\Gamma_a^2 + \Gamma_b^2}.$

Sind also X,Y zwei unabhängige Zufallsvariable mit

$X \sim \mathcal N(\mu_X,\sigma_X^2),\ Y \sim \mathcal N(\mu_Y,\sigma_Y^2),$

so ist deren Summe ebenfalls normalverteilt:

$X+Y \sim \mathcal N(\mu_X+\mu_Y,\sigma_X^2+\sigma_Y^2).$

Das lässt sich dadurch beweisen, dass die charakteristische Funktion der Summe das Produkt der charakteristischen Funktionen der Summanden ist.

Speziell ist das arithmetische Mittel n unabhängiger und normalverteilter Zufallsgrößen 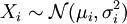$X_i \sim \mathcal N(\mu_i, \sigma_i^2)$ wieder eine normalverteilte Zufallsgröße mit

$Z \sim \mathcal N(\frac 1n \sum_{i=1}^n \mu_i, \frac 1{n^2} \sum_{i=1}^n \sigma_i^2).$

Nach dem Satz von Cramér gilt sogar die Umkehrung: Ist eine normalverteilte Zufallsgröße die Summe von unabhängigen Zufallsgrößen, dann sind die Summanden ebenfalls normalverteilt.

Die Dichtefunktion der Normalverteilung ist ein Fixpunkt der Fourier-Transformation, d. h. die Fourier-Transformierte einer Gaußkurve ist wieder eine Gaußkurve. Das Produkt der Standardabweichungen dieser korrespondierenden Gaußkurven ist konstant; es gilt die heisenbergsche Unschärferelation.

Entropie

Die Normalverteilung hat die Entropie: $\log\left(\sigma\sqrt{2\,\pi\,e}\right)\!$.

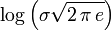Da sie für eine gegebene Varianz die größte Entropie unter allen Verteilungen hat, wird sie in der Maximum-Entropie-Methode oft als a-priori-Wahrscheinlichkeit verwendet.

Mehrdimensionale Verallgemeinerung

Dichte der zweidimensionalen Normalverteilung; die Standardabweichung der zweiten Koordinate Y ist 2, die Korrelation zwischen den Koordinaten 0,7

Das Wahrscheinlichkeitsmaß 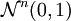$\mathcal N^n(0,1)$ auf $\R^n$, das durch die Dichtefunktion

$f_X: \R^n \to \R,\,(x_1,\ldots,x_n) \mapsto \frac 1{\sqrt{(2\pi)^n}} \exp\left( -\frac 12 \sum_{i=1}^n x_i^2 \right)$

definiert wird, heißt Standardnormalverteilung der Dimension n. Ein Zufallsvektor 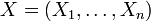$X = (X_1,\ldots,X_n)$ ist genau dann standardnormalverteilt auf $\R^n$, wenn seine Komponenten 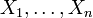$X_1,\ldots,X_n$ standardnormalverteilt und stochastisch unabhängig sind.

Die multivariate Standardnormalverteilung ist abgesehen von Translationen (d. h. Erwartungswert 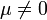$\mu\ne0$) die einzige multivariate Verteilung, deren Komponenten stochastisch unabhängig sind und deren Dichte zugleich rotationssymmetrisch ist.

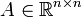Ein Wahrscheinlichkeitsmaß P auf $\R^n$ heißt n-dimensionale Normalverteilung, wenn eine Matrix $A \in \R^{n \times n}$ und ein Vektor 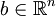$b \in \R^n$ existieren, sodass mit der affinen Abbildung 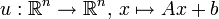$u: \R^n \to \R^n,\,x \mapsto Ax+b$ gilt:

$u^{-1}(P) = \mathcal N^n(0,1).$

Die Dichtefunktion der zweidimensionalen Normalverteilung mit einem Korrelationskoeffizienten 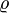$\varrho$ ist

$f_X(x_1,x_2) = \frac 1{2\pi\sigma_1\sigma_2\sqrt{1-\varrho^2}} \exp\left( -\frac 1{2(1-\varrho^2)} \left( \left(\frac{x_1-\mu_1}{\sigma_1}\right)^2 - 2\varrho\,\frac{x_1-\mu_1}{\sigma_1} \frac{x_2-\mu_2}{\sigma_2} + \left(\frac{x_2-\mu_2}{\sigma_2}\right)^2 \right) \right)$

und schließlich im n-dimensionalen Fall

$f_X(x_1, \ldots, x_n) = \frac 1 {(2\pi)^{n/2} \left|\Sigma\right|^{1/2}} \exp \left( -\frac 12 (x-\mu)^\top \Sigma^{-1} (x-\mu) \right)$

mit | Σ | als der Determinante der Kovarianzmatrix Σ.

Beziehungen zu anderen Verteilungsfunktionen

Transformation zur Standardnormalverteilung (z-Transformation)

Ist eine Normalverteilung mit beliebigen μ und σ gegeben, so kann diese durch eine Transformation auf eine 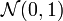$\mathcal{N}(0,1)$-Normalverteilung zurückgeführt werden. Dazu wird die Verteilungsfunktion F(x) der allgemeinen Normalverteilung mit 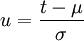$u=\frac{t-\mu}{\sigma}$ substituiert und die Integralgrenzen werden angepasst:

Nebenrechnung für die Substitution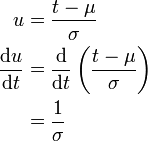

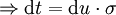
$\begin{align} u &= \frac{t-\mu}\sigma\\ \frac{\mathrm du}{\mathrm dt}&= \frac{\mathrm d}{\mathrm dt} \left(\frac{t-\mu}\sigma\right)\\ &= \frac 1\sigma \end{align}$ $\Rightarrow \mathrm dt=\mathrm du \cdot \sigma$

$\begin{align} F(x) &= \frac 1{\sigma \cdot \sqrt{2\pi}} \cdot \int_{-\infty}^x \mathrm e^{-\frac 12 \cdot \left( \frac{t-\mu}{\sigma}\right)^2} \mathrm dt\\ &= \frac 1{\sigma \cdot \sqrt{2\pi}} \cdot \int_{\frac{-\infty-\mu}\sigma}^{\frac{x-\mu}\sigma} \mathrm e^{-\frac 12 u^2} \mathrm du \cdot \sigma\\ &= \frac 1{\sqrt{2\pi}} \cdot \int_{-\infty}^{\frac{x-\mu}\sigma} \mathrm e^{-\frac 12 u^2} \mathrm du\\ &= \Phi \left(\frac{x-\mu}{\sigma}\right) \end{align}$

Wird nun 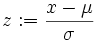$z:= \frac{x-\mu}{\sigma}$ definiert und u durch t ersetzt, so erhält man die Verteilungsfunktion der Standardnormalverteilung:

$\Phi(z)=\frac 1{\sqrt{2\pi}} \cdot \int_{-\infty}^z \mathrm e^{-\frac 12 t^2} \mathrm{d}t$

Geometrisch betrachtet entspricht die durchgeführte Substitution einer flächentreuen Transformation der Glockenkurve von 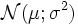$\mathcal{N}(\mu;\sigma^2)$ zur Glockenkurve von $\mathcal{N}(0;1)$.

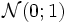Approximation der Binomialverteilung durch die Normalverteilung

Die Normalverteilung kann zur Approximation der Binomialverteilung verwendet werden, wenn der Stichprobenumfang n hinreichend groß und in der Grundgesamtheit der Anteil p der gesuchten Eigenschaft nicht zu klein ist. Als Faustregeln dafür gelten: 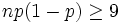$np(1-p)\geq 9$, was für die Standardabweichung bedeutet: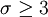 $\sigma\geq 3$

Falls diese Bedingung nicht erfüllt sein sollte, ist die Näherung immer noch vertretbar genau, wenn gilt: 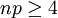$np\geq 4$ und zugleich $n(1-p)\geq 4$.

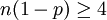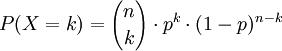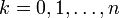Ist eine Binomialverteilung (Bernoulli-Versuch) mit n voneinander unabhängigen Stufen (bzw. Zufallsversuchen) mit einer Erfolgswahrscheinlichkeit p gegeben, so lässt sich die Wahrscheinlichkeit für k Erfolge allgemein durch $P(X=k)= {n \choose k} \cdot p^k\cdot (1-p)^{n-k}$ für $k=0,1,\dots,n$ berechnen.

Für sehr große Werte von n kann diese Binomialverteilung durch eine Normalverteilung approximiert werden (Satz von Moivre-Laplace, zentraler Grenzwertsatz). Dabei ist

• der Erwartungswert $\mu=n\cdot p$
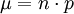
• und die Standardabweichung $\sigma=\sqrt{n \cdot p \cdot (1-p) }$

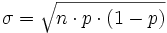
Ist nun σ > 3, dann ist folgende Näherung brauchbar:

$P(x_1 \leq X \leq x_2) = \underbrace{\sum_{k=x_1}^{x_2} {n \choose k} \cdot p^k\cdot (1-p)^{n-k}}_{\mathrm{BV}} \approx \underbrace{\Phi\left(\frac{x_2+0,5-\mu}{\sigma}\right) -\Phi\left(\frac{x_1-0,5-\mu}{\sigma}\right)}_{\mathrm{NV}}\,$

Bei der Normalverteilung wird die untere Grenze um 0,5 verkleinert und die obere Grenze um 0,5 vergrößert, um eine bessere Approximation bei einer geringen Standardabweichung σ gewährleisten zu können. Dies nennt man auch Stetigkeitskorrektur. Nur wenn σ einen sehr hohen Wert besitzt, kann auf sie verzichtet werden.

Da die Binomialverteilung diskret ist, muss auf einige Punkte geachtet werden:

• < oder 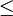$\leq$ (und auch größer und größer gleich) müssen beachtet werden (was ja bei der Normalverteilung nicht der Fall ist). Deshalb muss bei P(X_BV < x) die nächstkleinere natürliche Zahl gewählt werden, d. h.

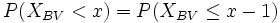$P(X_{BV}&amp;amp;lt;x)=P(X_{BV}\leq x-1)$ bzw. $P(X_{BV}&amp;amp;gt;x)=P(X_{BV}\geq x+1)$

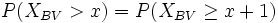
damit mit der Normalverteilung weitergerechnet werden kann.

z. B. $P(X_{BV}&amp;amp;lt;70)=P(X_{BV}\leq 69)$

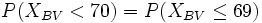
• Außerdem ist

$P(X_{BV} \leq x) = P(0 \leq X_{BV} \leq x)$

$P(X_{BV} \geq x) = P(x \leq X_{BV} \leq n)$

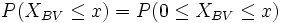
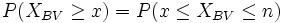
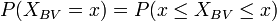$P(X_{BV} = x) = P(x \leq X_{BV} \leq x)$ (unbedingt mit Stetigkeitskorrektur)

und lässt sich somit durch die oben angegebene Formel berechnen.

Der große Vorteil der Approximation liegt darin, dass sehr viele Stufen einer Binomialverteilung sehr schnell und einfach bestimmt werden können.

Beziehung zur Cauchy-Verteilung

Der Quotient von zwei unabhängigen 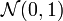$\mathcal{N}(0,1)$ standardnormalverteilten Zufallsvariablen ist Cauchy-verteilt.

Beziehung zur Chi-Quadrat-Verteilung

• Die Summe 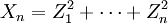$X_n=Z_1^2 + \cdots + Z_n^2$ von n unabhängigen quadrierten standardnormalverteilten Zufallsvariablen 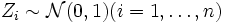$Z_i\sim \mathcal{N}(0,1) (i=1,\ldots,n)$ genügt einer Chi-Quadrat-Verteilung 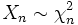$X_n\sim\chi^2_n$ mit n Freiheitsgraden.

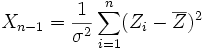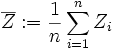• Die Summe $X_{n-1}=\frac{1}{\sigma^{2}}\sum_{i=1}^{n} (Z_{i}-\overline Z)^{2}$ mit $\overline Z:=\frac{1}{n}\sum_{i=1}^{n} Z_i$ und n unabhängigen normalverteilten Zufallsvariablen 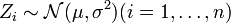$Z_i\sim \mathcal{N}(\mu,\sigma^{2}) (i=1,\ldots,n)$ genügt einer Chi-Quadrat-Verteilung 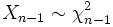$X_{n-1}\sim\chi^2_{n-1}$ mit n − 1 Freiheitsgraden.

Die Chi-Quadrat-Verteilung wird zur Konfidenzschätzung für die Varianz einer normalverteilten Grundgesamtheit verwendet.

Beziehung zur Rayleigh-Verteilung

Der Betrag 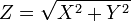$Z = \sqrt{X^2 + Y^2}$ zweier normalverteilter Zufallsvariablen X,Y ist Rayleigh-verteilt.

Beziehung zur logarithmischen Normalverteilung

Ist die Zufallsvariable X normalverteilt mit 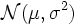$\mathcal{N}(\mu,\sigma^{2})$, dann ist die Zufallsvariable Y = e^X logarithmisch-normalverteilt mit $\mathcal{LN}(\mu,\sigma^{2})$.

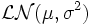Die Entstehung einer logarithmischen Normalverteilung ist auf multiplikatives, die einer Normalverteilung auf additives Zusammenwirken vieler Zufallsgrößen zurückführen.

Beziehung zur F-Verteilung

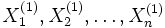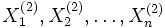Wenn die identischen normalverteilten Zufallsvariablen $X_1^{(1)}, X_2^{(1)}, \dots , X_n^{(1)}$ und $X_1^{(2)}, X_2^{(2)}, \dots , X_n^{(2)}$ die Parameter

$E(X_{i}^{(1)})=\mu_{1}, \sqrt{Var(X_{i}^{(1)})}=\sigma_{1}$

$E(X_{i}^{(2)})=\mu_{2}, \sqrt{Var(X_{i}^{(2)})}=\sigma_{2}$

mit σ₁ = σ₂ = σ besitzen, dann unterliegt die Zufallsvariable

$Y_{n_{1}-1,n_{2}-1}:=\frac{(n_{2}-1)\sum\limits_{i=1}^{n_{1}}(X_{i}^{(1)}-\bar{{X}}^{(1)})^{2}} {(n_{1}-1)\sum\limits_{j=1}^{n_{2}}(X_{i}^{(2)}-\bar{{X}}^{(2)})^{2}}$

einer F-Verteilung mit ((n₁ − 1,n₂ − 1)) Freiheitsgraden. Dabei sind

$\bar{X}^{(1)}=\frac{1}{n_{1}}\sum_{i=1}^{n_{1}}X_{i}^{(1)}\quad \bar{X}^{(2)}=\frac{1}{n_{2}}\sum_{i=1}^{n_{2}}X_{i}^{(2)}$.

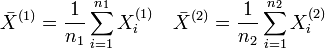Beziehung zur Student-t-Verteilung

Wenn die unabhängigen Zufallsvariablen 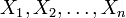$X_1, X_2, \dots , X_n$ identisch normalverteilt sind mit den Parametern μ und σ, dann unterliegt die stetige Zufallsgröße

$Y_{n-1}=\frac{\bar{X}-\mu}{\displaystyle\sqrt{\frac{\sum_{i=1}^{n}(X_{i}-\bar{X})^{2}}{n-1}}}\sqrt{n}$

einer Student-t-Verteilung mit (n − 1) Freiheitsgraden.

Die Student-t-Verteilung wird zur Konfidenzschätzung für den Erwartungswert einer normalverteilten Zufallsvariable bei unbekannter Varianz verwendet.

Rechnen mit der Standardnormalverteilung

Bei Aufgabenstellungen, bei denen die Wahrscheinlichkeit für normalverteilte Zufallsvariablen durch die Standardnormalverteilung ermittelt werden soll, ist es nicht nötig, die oben angegebene Transformation jedes Mal durchzurechnen. Stattdessen wird einfach das Ergebnis der Transformation verwendet, um die Grenzen x₁, x₂ und die Zufallsvariable X auf die Grenzen z₁, z₂ und die Zufallsvariable Z anzugleichen. Somit kann eine 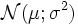$\mathcal{N}(\mu;\sigma^2)$ Verteilung durch

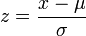$z=\frac {x-\mu}{\sigma}$   beziehungsweise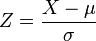   $Z=\frac {X-\mu}{\sigma}$

zu 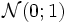$\mathcal{N}(0;1)$ transformiert werden.

Die Wahrscheinlichkeit für ein Ereignis, welches z. B. innerhalb der Werte x₁ und x₂ (für den Erwartungswert μ und die Standardabweichung σ) liegt, ist durch folgende Umrechnung gleich der Wahrscheinlichkeit der Standardnormalverteilung mit den neuen Grenzen z₁ und z₂:

$P( x_1 \leq X \leq x_2 ) = P\left( \frac {x_1-\mu}{\sigma} \leq Z= \frac {X-\mu}{\sigma} \leq \frac {x_2-\mu}{\sigma}\right)= P(z_1 \leq Z \leq z_2)$

P steht für die englische Bezeichnung „probability“ oder das französische Wort „probabilité“ der Wahrscheinlichkeit.

Grundlegende Fragestellungen

Allgemein gibt die Verteilungsfunktion die Fläche unter der Glockenkurve bis zum Wert x an, d. h. es wird das bestimmte Integral von 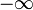$-\infty$ bis x berechnet.

Dies entspricht in Aufgabenstellungen einer gesuchten Wahrscheinlichkeit, bei der die Zufallsvariable X kleiner oder kleiner gleich einer bestimmten Zahl x ist. Durch die Verwendung der reellen Zahlen und der Stetigkeit der Normalverteilung macht es keinen Unterschied, ob nun < oder 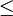$\leq$ verlangt ist,

weil 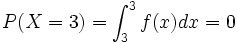$P(X = 3) = \int_3^3 f(x)dx = 0$ und somit $P(X&amp;amp;lt;3) = P(X \leq 3)$.

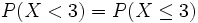Dasselbe gilt für größer und größer gleich.

Dadurch, dass X nur kleiner oder größer einer Grenze (oder innerhalb oder außerhalb zweier Grenzen) liegen kann, ergeben sich für Aufgaben bei normalverteilten Wahrscheinlichkeitsberechnungen folgende zwei grundlegende Fragestellungen:

• Wie hoch ist die Wahrscheinlichkeit, dass bei einem Zufallsversuch die normalverteilte Zufallsvariable Z höchstens den Wert z annimmt?

  $P(Z \leq z)=\Phi(z)$

In der Schulmathematik wird für diese Aussage auch die Bezeichnung Linker Spitz verwendet, da die Fläche unter der Gaußkurve von links bis zur Grenze verläuft. Für z sind auch negative Werte erlaubt, trotzdem haben viele Tabellen der Standardnormalverteilung nur positive Einträge. Durch die Symmetrie der Kurve und der Negativitätsregel des linken Spitz stellt dies aber keine Einschränkung dar:

$\Phi(-z)\ =\ 1-\Phi(z)$

• Wie hoch ist die Wahrscheinlichkeit, dass bei einem Zufallsversuch die normalverteilte Zufallsvariable Z mindestens den Wert z annimmt?

$P(Z \geq z) = 1 - \Phi(z)$

Analog wird hier oft die Bezeichnung Rechter Spitz verwendet. Ebenso gibt es eine Negativitätsregel:

$P(Z \geq -z)= 1- \Phi(-z)= 1-(1-\Phi(z)) = \Phi(z)$

(Da jede Zufallsvariable X der allgemeinen Normalverteilung sich in die Zufallsgröße Z der Standardnormalverteilung umwandeln lässt, gelten die Fragestellungen für beide Größen gleichbedeutend.)

Streubereich und Antistreubereich

Der Streubereich gibt die Wahrscheinlichkeit wieder, dass die normalverteilte Zufallsvariable Z Werte zwischen z₁ und z₂ annimmt:

$P(z_1 \le Z \le z_2) = \Phi(z_2) - \Phi(z_1)$

Beim Sonderfall des symmetrischen Streubereiches (z₁ = − z₂, mit z₂ > 0) gilt

$\begin{align} P(-z\le Z\le z ) &amp;amp;amp;= P (|Z|\le z)\\ &amp;amp;amp;= \Phi(z)-\Phi(-z)\\ &amp;amp;amp;= \Phi(z)-(1-\Phi(z))\\ &amp;amp;amp;= 2\Phi(z)-1. \end{align}$

Hingegen gibt der Antistreubereich die Höhe der Wahrscheinlichkeit an, dass die normalverteilte Zufallsvariable Z Werte außerhalb des Bereichs zwischen z₁ und z₂ annimmt:

$P(Z\le z_1\text{ oder }Z\ge z_2) = \Phi(z_1) + (1-\Phi(z_2)).$

Somit folgt bei einem symmetrischen Antistreubereich

$\begin{align} P(Z\le -z\text{ oder }Z\ge z) &amp;amp;amp;= P(|Z|\ge z)\\ &amp;amp;amp;=\Phi(-z)+1-\Phi(z)\\ &amp;amp;amp;= 1-\Phi(z)+1-\Phi(z)\\ &amp;amp;amp;=2-2 \Phi(z) \end{align}$

Streubereiche am Beispiel der Qualitätssicherung

Besondere Bedeutung haben beide Streubereiche z. B. bei der Qualitätssicherung von technischen oder wirtschaftlichen Produktionsprozessen. Hier gibt es einzuhaltende Toleranzgrenzen x₁ und x₂ , wobei es meist einen größten noch akzeptablen Abstand ε vom Erwartungswert μ (= dem optimalen Sollwert) gibt. σ kann hingegen empirisch aus dem Produktionsprozess gewonnen werden.

Wurde [x₁;x₂] = [μ − ε;μ + ε] als einzuhaltendes Toleranzintervall angegeben, so liegt (je nach Fragestellung) ein symmetrischer Streu- oder Antistreubereich vor.

Im Falle des Streubereiches gilt:

$P(x_1 \leq X \leq x_2) = P(|X-\mu|\leq\epsilon)=$

$=P(\mu-\epsilon \leq X \leq \mu+\epsilon) = P\left(\frac{-\epsilon}{\sigma} \leq Z \leq \frac{\epsilon}{\sigma}\right)=$

$=\Phi\left(\frac{\epsilon}{\sigma}\right)-\Phi\left(\frac{-\epsilon}{\sigma}\right)=$

$= 2 \cdot \Phi\left(\frac{\epsilon}{\sigma}\right)-1 =\gamma$

Der Antistreubereich ergibt sich dann aus

$P(|X-\mu|\geq \epsilon )= 1-\gamma$

oder wenn kein Streubereich berechnet wurde durch

$P(|X-\mu|\geq \epsilon )=2\cdot\left(1-\Phi\left(\frac{\epsilon} {\sigma}\right)\right)=\alpha$.

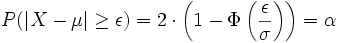Das Ergebnis γ ist also die Wahrscheinlichkeit für verkaufbare Produkte, während α die Wahrscheinlichkeit für Ausschuss bedeutet, wobei beides von den Vorgaben von μ, σ und ε abhängig ist.

Ist bekannt, dass die maximale Abweichung ε symmetrisch um den Erwartungswert liegt, so sind auch Fragestellungen möglich, bei denen die Wahrscheinlichkeit vorgegeben und eine der anderen Größen zu berechnen ist.

Testen auf Normalverteilung

Quantile einer Normalverteilung und einer Chi-Quadrat-Verteilung

Um zu überprüfen, ob vorliegende Daten normalverteilt sind, können folgende Methoden angewandt werden:

• Chi-Quadrat-Test
• Kolmogorov-Smirnov-Test
• Anderson-Darling-Test (Modifikation des Kolmogorov-Smirnov-Tests)
• Lilliefors-Test (Modifikation des Kolmogorov-Smirnov-Tests)
• Shapiro-Wilk-Test
• Jarque-Bera-Test
• Q-Q-Plot (deskriptive Überprüfung)
• Maximum-Likelihood-Methode (deskriptive Überprüfung)

Die Tests haben unterschiedliche Eigenschaften hinsichtlich der Art der Abweichungen von der Normalverteilung, die sie erkennen. So erkennt der Kolmogorov-Smirnov-Test Abweichungen in der Mitte der Verteilung eher als Abweichungen an den Rändern, während der Jarque-Bera-Test ziemlich sensibel auf stark abweichende Einzelwerte an den Rändern („heavy tails“) reagiert.

Beim Lilliefors-Test muss im Gegensatz zum Kolomogorov-Smirnov-Test nicht standardisiert werden, d. h. μ und σ der angenommenen Normalverteilung dürfen unbekannt sein.

Mit Hilfe von Quantil-Quantil-Plots (auch Normal-Quantil-Plots oder kurz Q-Q-Plot) ist eine einfache grafische Überprüfung auf Normalverteilung möglich.
Mit der Maximum-Likeliehood-Methode können die Parameter μ und σ der Normalverteilung geschätzt und die empirischen Daten mit der angepassten Normalverteilung grafisch verglichen werden.

Simulation normalverteilter Zufallsvariablen

Box-Muller-Methode

Nach der Box-Muller-Methode lässt sich eine standardnormalverteilte Zufallsvariable X aus zwei gleichverteilten Zufallsvariablen 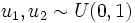$u_1,u_2 \sim U(0,1)$, sogenannten Standardzufallszahlen, simulieren:

$X=\cos(2 \pi u_1) \cdot \sqrt{-2\ln u_2}$

Polar-Methode

Die Polar-Methode von Marsaglia ist auf einem Computer noch schneller, da sie nur einen Logarithmus benutzt:

1. Erzeuge zwei voneinander unabhängige, im Intervall [ − 1,1] gleichverteilte Zufallszahlen u₁,u₂
2. Berechne 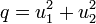$q=u_1^2+u_2^2$. Falls q > 1, wiederhole Schritt 1.
3. Berechne $p = \sqrt {-2 \cdot \ln q / q }$
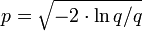
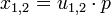4. $x_{1,2}=u_{1,2} \cdot p$ liefert zwei voneinander unabhängige, standardnormalverteilte Zufallszahlen x_1,2.

Durch lineare Transformation lassen sich hieraus beliebige normalverteilte Zufallszahlen erzeugen: Ist die Zufallsvariable 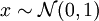$x \sim \mathcal{N}(0,1)$-verteilt, so ist 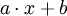$a \cdot x + b$ schließlich 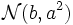$\mathcal{N}(b,a^2)$-verteilt.

Zwölferregel

Der zentrale Grenzwertsatz besagt, dass sich unter bestimmten Voraussetzungen die Verteilung der Summe unabhängiger, identisch verteilter Zufallszahlen einer Normalverteilung nähert.

Ein Spezialfall ist die Zwölferregel, die sich auf die Summe von zwölf Zufallszahlen aus einer Gleichverteilung auf dem Intervall [0,1] beschränkt und bereits zu passablen Verteilungen führt.

Stark ins Gewicht fällt die Forderung der Unabhängigkeit der zwölf Zufallsvariablen X_i, die bei normalen Pseudozufallszahlen (LKG) nicht garantiert ist. Im Gegenteil wird vom Spektraltest meist nur die Unabhängigkeit von maximal vier bis sieben der X_i garantiert. Für numerische Simulationen ist die Zwölferregel daher sehr bedenklich. Andere, sogar leichter zu programmierende Verfahren, sind daher vorzuziehen.

Verwerfungsmethode

Normalverteilungen lassen sich mit der Verwerfungsmethode (s. dort) simulieren.

Inversionsmethode

Die Normalverteilung lässt sich auch mit der Inversionsmethode berechnen. Da das Fehlerintegral leider nicht explizit mit elementaren Funktionen integrierbar ist, muss man auf Reihenentwicklungen der inversen Funktion für einen Startwert (a₁...a₁₄ weiter unten) und anschließende Korrektur mit dem Newtonverfahren zurückgreifen. Dazu werden erf(x) und erfc(x) benötigt, die ihrerseits mit Reihenentwicklungen und Kettenbruchentwicklungen berechnet werden können - insgesamt ein relativ hoher Aufwand. Die notwendigen Entwicklungen sind in der Literatur zu finden.^[2]

Entwicklung des inversen Fehlerintegrals (wegen des Pols nur als Startwert für das Newtonverfahren verwendbar):

$\operatorname{erf}^{-1} \left(\frac{\sqrt\pi}2 x\right) = x\Bigl(a_1 + x^2 \bigl(a_2 + x^2 (\dots)\bigr)\Bigr)$

mit den Koeffizienten

$\begin{align} a_i &amp;amp;amp;= 1, \frac 13, \frac 7{30}, \frac {127}{630}, \frac {4369}{22680}, \frac {34807}{178200}, \frac {20036983}{97297200}, \frac {2280356863}{10216206000}, \frac {49020204823}{198486288000},\\ &amp;amp;amp; {65967241200001\over 237588086736000}, {15773461423793767\over 49893498214560000}, {655889589032992201\over 1803293578326240000},\\ &amp;amp;amp; {94020690191035873697\over 222759794969712000000}, {655782249799531714375489\over 1329207696584271504000000},\ldots \end{align}$

Simulation mehrdimensionaler normalverteilter Zufallsvektoren

Die Komponenten des Zufallsvektors X ^* werden durch standardnormalverteilte Zufallsvariable gefüllt (diese lassen sich mit einem der obigen Verfahren erzeugen). Dann ist der Zufallsvektor

X = UX ^* + μ

eine Realisierung der Normalverteilung mit Erwartungswertvektor μ und Kovarianzmatrix 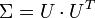$\Sigma=U\cdot U^T$. U wird dabei durch die Cholesky-Zerlegung berechnet.

Plausibilisierung:

Erwartungswert:

$E(X) = E(U X^* + \mu) = \underbrace{E(UX^*)}_{=0} + E(\mu) = \mu$

Kovarianz:

$\begin{align} \operatorname{cov}(X) &amp;amp;amp;= \frac 1n \sum_{i=1}^n (X_i-\mu) (X_i-\mu)^T\\ &amp;amp;amp;= \frac 1n \sum_{i=1}^n U X_i^* X_i^{*T} U^T\\ &amp;amp;amp;= U\underbrace{\left(\frac 1n \sum_{i=1}^n X_i^* X_i^{*T} \right)}_{=\operatorname{cov}(X^*)=I} U^T\\ &amp;amp;amp;= U U^T\\ &amp;amp;amp;= \Sigma \end{align}$

Anwendungen außerhalb der Wahrscheinlichkeitsrechnung

Die Normalverteilung lässt sich auch zur Beschreibung nicht direkt stochastischer Sachverhalte verwenden, etwa in der Physik für das Amplitudenprofil der Gauß-Strahlen und andere Verteilungsprofile.

Zudem findet sie Verwendung in der Gabor-Transformation.

Siehe auch

• Additives weißes gaußsches Rauschen
• Wahrscheinlichkeitsnetz
• Statistik

Quellen

1. ↑ Bei der Funktion exp(x) handelt es sich um die Exponentialfunktion mit der Basis e, auch als e^x bekannt.
2. ↑ William B. Jones, W. J. Thron; Continued Fractions: Analytic Theory and Applications; Addison Wesley, 1980

Weblinks

• Darstellung mit Programmcode in Visual Basic

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | Zeta

 

Kontinuierliche univariate Verteilungen

Kontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-Halbkreis

Kontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambda

Kontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | Voigt

 

Multivariate Verteilungen

Diskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet Multinomial

Kontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-Gamma

Multivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart