Bitweiser Operator

In der Informatik ist ein bitweiser Operator ein Operator, der auf ein oder zwei Bitfolgen oder Binärzahlen auf der Ebene einzelner Bits angewendet wird. Auf vielen Computern sind bitweise Operationen etwas schneller als Additions- und Subtraktionsoperationen und deutlich schneller als Multiplikations- und Divisionsoperationen.

Bitweise Operatoren

NICHT

Ein bitweises NICHT oder Komplement ist eine einstellige Verknüpfung, die eine logische Negation jedes Bits durchführt und damit das Einerkomplement einer Binärzahl bildet. Jede 0 wird durch eine 1 ausgetauscht und umgekehrt. Beispiel:

NICHT 0111
    = 1000

In vielen Programmiersprachen der C-Familie wird das bitweise NICHT als „~“ (Tilde) dargestellt. Dieser Operator darf nicht mit dem Operator für „logisches NICHT“ „!“ (Ausrufezeichen) verwechselt werden, der den gesamten Wert als Booleschen Ausdruck interpretiert und true oder false zurückgibt. Das „logische NICHT“ ist keine bitweise Operation.

NICHT (Logisch): !1d = 0d; !5d = 0d
NICHT (Bitweise): ~1d = 0d; ~5d = ~0101b = 1010b = 10d

ODER

Ein bitweises ODER wird auf zwei Bitfolgen gleicher Länge angewendet und gibt eine Bitfolge derselben Länge zurück, indem es jeweils Bits an der gleichen Stelle (jeweils das erste Bit, jeweils das zweite Bit usw.) mit einem logischen ODER (logische Disjunktion) verknüpft. Bei jedem Paar ist das Ergebnisbit 1, falls das Bit der ersten Bitfolge 1 ist ODER das Bit der zweiten Bitfolge 1 ist, ansonsten ist das Ergebnisbit 0. Beispiel:

     0101
ODER 0011
   = 0111

In den mit C verwandten Programmiersprachen wird das bitweise ODER durch „|“ (senkrechter Strich) dargestellt. Dieser Operator darf nicht mit seinem booleschen Gegenstück verwechselt werden, das seine Operanden als boolesche Werte interpretiert und als „||“ (zwei senkrechte Striche) dargestellt wird.

Das bitweise ODER wird verwendet, wenn mehrere Bits als Flags verwendet werden; die Bits einer einzelnen Binärzahl können jeweils eine eigene boolesche Variable darstellen. Wendet man das bitweise ODER auf einen solchen Binärwert und eine „Maske“ an, die an bestimmten Stellen eine 1 enthält, so erhält man eine neue Bitfolge, in der diese Bits zusätzlich zu den ursprünglich vorhandenen gesetzt sind. Beispiel:

0010

kann als Liste von vier Flags angesehen werden. Das erste, zweite und vierte Flag sind nicht gesetzt (0), das dritte Flag ist gesetzt (1). Das erste Flag kann gesetzt werden, indem man diese Bitfolge mit einer Bitfolge verknüpft, die nur an der ersten Stelle eine 1 hat:

   0010
OR 1000
 = 1010

Diese Technik wird eingesetzt, um Speicherplatz zu sparen, wenn Programme sehr viele Boolesche Werte verwalten müssen.

XOR

Ein bitweises exklusives ODER wird auf zwei Bitfolgen der gleichen Länge angewendet und führt die logische XOR-Operation auf jedem Paar korrespondierender Bits durch. Das Ergebnisbit ist 1, falls die zwei Bits unterschiedlich sind, und 0, falls sie gleich sind. Beispiel:

    0101
XOR 0011
  = 0110

In den mit C verwandten Programmiersprachen wird das bitweise XOR als „^“ (Circumflex) dargestellt.

In der Assemblersprache wird das bitweise XOR gelegentlich eingesetzt, um den Wert eines Prozessorregisters auf 0 zu setzen. Wendet man XOR auf zwei identische Operanden an, so erhält man immer 0. In vielen Architekturen benötigt diese Operation weniger Rechenzeit, als man für das Laden einer 0 und das Speichern im Register benötigt.

Das bitweise XOR kann auch verwendet werden, um Flags in Bitfolgen umzuschalten. Beispiel:

0010

Das erste und das dritte Bit können simultan umgeschaltet werden, indem man diese Bitfolge mit XOR mit einer Maske verknüpft, welche die Bits 1 und 3 gesetzt hat:

    0010
XOR 1010
  = 1000

Diese Technik kann eingesetzt werden, um Bitfolgen zu manipulieren, die mehrere boolesche Variablen repräsentieren.

UND

Ein bitweises UND wird auf zwei Bitfolgen gleicher Länge angewendet und führt die logische UND-Verknüpfung (logische Konjunktion) auf jedem Paar korrespondierender Bits durch. Das Ergebnisbit ist 1, falls beide Bits 1 sind, ansonsten 0. Beispiel:

    0101
UND 0011
  = 0001

In den mit C verwandten Programmiersprachen wird das bitweise UND durch „&“ (kaufmännisches Und, engl. 'ampersand') dargestellt. Dieser Operator darf nicht mit seinem booleschen Gegenstück verwechselt werden, das seine Operanden als boolesche Werte interpretiert und als „&&“ (zwei kaufmännische Und) dargestellt wird.

Das bitweise UND kann verwendet werden, um eine Bitfolge zu maskieren. Dadurch können Teile eines Bitstrings isoliert werden, und man kann bestimmen, ob ein bestimmtes Bit gesetzt ist oder nicht. Beispiel:

0011

Um herauszufinden, ob das dritte Bit gesetzt ist oder nicht, wird darauf ein bitweises UND mit einer Maske angewendet, die an der dritten Position eine 1 enthält:

    0011
UND 0010
  = 0010

Da das Ergebnis nicht Null ist, muss das dritte Bit in der ursprünglichen Bitfolge eine 1 gewesen sein. Diese Anwendung des bitweisen UND wird bitweise Maskierung genannt, weil Teile, die nicht geändert werden sollen oder für die Berechnung nicht wichtig sind, ausgeblendet werden.

Das bitweise UND kann mit dem bitweisen NICHT kombiniert werden, um Bits zu löschen. Beispiel:

0110 

Das zweite Flag kann gelöscht (d.h. auf 0 gesetzt) werden, indem darauf das bitweise UND mit einer Maske angewendet wird, die das Komplement einer Bitfolge darstellt, die nur an der zweiten Position eine 1 enthält:

NICHT 0100
    = 1011

      0110
  UND 1011
    = 0010

Bitweise Verschiebungen

Bitweise Verschiebungen (engl. bitwise shift) werden manchmal ebenfalls als bitweise Operationen aufgefasst, weil sie auf der binären Ebene statt auf dem numerischen Wert einer Variable arbeiten; bitweise Verschiebungen arbeiten jedoch nicht auf Paaren von korrespondierenden Bits und sind damit nicht bitweise im ursprünglichen Sinn. Schaltungstechnisch können bitweise Verschiebungen und Rotationen um eine beliebige Stellenanzahl in Form von Barrel-Shiftern realisiert werden.

Bei diesen Operationen werden die Ziffern nach links oder rechts verschoben. Register der Prozessoren haben eine begrenzte Anzahl zur Verfügung stehender Speicherplätze, weshalb einige Bits an einem Ende aus dem Register „hinausgeschoben“ werden, während die gleiche Anzahl an Bits am anderen Ende „hineingeschoben“ wird. Der Unterschied zwischen den bitweisen Verschiebungsoperatoren besteht in der Berechnung der Bits, die auf diese Weise „hineingeschoben“ werden.

Dieses Verfahren ermöglicht somit den Zugriff auf einzelne Bits einer Null-Eins-Abfolge und stellt eine Alternative zur Multiplikation bzw. Division dar.

Beispiel

Symbolik:

• „<<“ Verschieben nach links,
• „>>“ Verschieben nach rechts, um den jeweils dahinter angegeben Wert
• „>>>“ ist eine Sonderform von „>>“; linke Seite wird mit Nullen aufgefüllt.

In Sprachen wie C wird für Rechtsverschiebungen abhängig vom Datentyp und ggf. Vorzeichen entweder mit Nullen (unsigned oder nicht-negativ) oder mit Einsen (signed und kleiner Null) aufgefüllt.

01001111 <<  1 = 10011110
00111100 <<  2 = 11110000
01001111 >>  1 = 00100111
11110000 >>  2 = 11111100 (signed)
11110000 >>  2 = 00111100 (unsigned)
01001111 >>> 1 = 00100111
11110000 >>> 2 = 00111100

Eine arithmetische Verschiebung um n ist äquivalent zu einer Multiplikation mit 2ⁿ.

12(dezimal) = 00001100 << 2 = 00110000 = 48(dezimal) = 2² * 12 = 4 * 12

Arithmetische Verschiebung

Arithmetischer Linksshift

Arithmetischer Rechtsshift

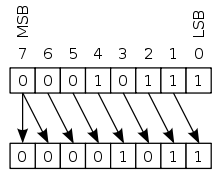
Bei einer arithmetischen Verschiebung (engl. arithmetic shift) werden die hinausgeschobenen Bits abgeschnitten. Bei einer Verschiebung nach links werden auf der rechten Seite Nullen nachgeschoben; bei einer Verschiebung nach rechts werden Kopien des Vorzeichenbits auf der linken Seite eingeschoben. Beispiel (4-Bit-Register):

  0110 LINKS-SHIFT
= 1100

  1100 RECHTS-SHIFT
= 1110

Bei der Linksverschiebung wird das am weitesten links stehende Bit aus dem Register hinausgeschoben und eine neue 0 am rechten Ende eingefügt. Bei der Rechtsverschiebung wird das am weitesten rechts stehende Bit hinausgeschoben (eventuell in ein Überlaufflag) und das ursprünglich höchstwertige Bit (MSB) am linken Ende eingefügt, wodurch das Vorzeichen der Zahl erhalten bleibt. Manchmal werden mehrere Verschiebungen zu einer Verschiebung um mehrere Stellen zusammengefasst.

Eine arithmetische Verschiebung um n ist äquivalent zu einer Multiplikation mit 2ⁿ (unter der Voraussetzung, dass kein Überlauf auftritt). Eine arithmetische Verschiebung einer Zweierkomplementzahl um n nach rechts entspricht einer Division durch 2ⁿ und Rundung auf die nächstkleinere Zahl.

Logische Verschiebung

→ Hauptartikel: Logische Verschiebung

Logischer Rechtsshift

Logischer Linksshift

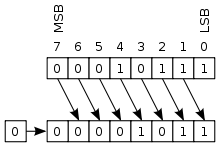
Bei einer logischen Verschiebung (engl. logic shift) werden die hinausgeschobenen Bits verworfen und Nullen eingeschoben, unabhängig von Schieberichtung und Vorzeichen. Deshalb sind logische und arithmetische Verschiebung nach links identische Operationen. Bei der logischen Verschiebung nach rechts werden jedoch Nullen statt Kopien des Vorzeichenbits eingefügt. Daher wird die logische Verschiebung bei vorzeichenlosen Binärzahlen eingesetzt, während arithmetische Verschiebungen bei vorzeichenbehafteten Zweierkomplementzahlen verwendet werden.

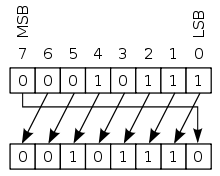
Zyklische Verschiebung ohne Übertragsbit

Zyklischer Rechtsshift

Zyklischer Linksshift

Eine andere Form der bitweisen Verschiebung ist die zyklische Verschiebung (engl. circular shift) oder bitweise Rotation. Bei dieser Operation „rotieren“ die Bits, als ob das linke und das rechte Ende verbunden wären. Das Bit, das hineingeschoben wird, hat denselben Wert wie das Bit, das aus dem Register hinausgeschoben wird. Diese Operation erhält alle existierenden Bits und wird teilweise in der digitalen Kryptographie eingesetzt, beispielsweise beim AES-Verfahren, von und nach seinen Entwicklern auch „Rijndael“ genannt. In elementarer Form, jedoch nicht auf Bitebene sondern auf der Basis eines Alphabets, wird sie in der Verschiebechiffre angewendet.

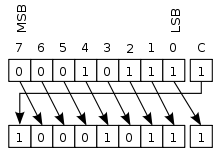
Zyklische Verschiebung mit Übertragsbit

Zyklischer Rechtsshift mit Übertragsbit C (Carry)

Zyklischer Linksshift mit Übertragsbit C (Carry)

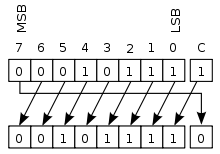
Zyklische Verschiebung mit Übertragsbit (engl. rotate through carry) funktioniert ähnlich wie die zyklische Verschiebung ohne Übertragsbit, jedoch werden die beiden Enden des Registers behandelt, als ob sie durch das Übertragsbit getrennt werden. Das Carry-Bit wird in das Register hineingeschoben, das aus dem Register hinausgeschobene Bit wird zum neuen Übertragsbit.

Eine einzelne zyklische Verschiebung mit Übertragsbit kann eine logische oder arithmetische Verschiebung um eine Stelle simulieren, wenn das Übertragsbit vorher entsprechend gesetzt wird. Enthält das Übertragsbit beispielsweise eine 0, dann entspricht die Verschiebung nach rechts einer arithmetischen Verschiebung nach rechts. Aus diesem Grund sind bei manchen Mikroprozessoren wie dem PICmicro nur Befehle für die beiden zyklischen Verschiebungsoperationen implementiert, es gibt keine speziellen Befehle für arithmetische oder logische Verschiebungen.

Zyklische Verschiebung mit Übertragsbit ist besonders nützlich, wenn Verschiebungen mit Zahlen durchgeführt werden, die größer als die Wortbreite des Prozessors sind, weil die Zahl dann in zwei Registern gespeichert wird und das aus einem Register hinausgeschobene Bit in das andere Register hineingeschoben werden muss. Bei zyklischer Verschiebung mit Übertragsbit wird dieses Bit bei der ersten Verschiebung im Übertragsbit „gespeichert“ und bei der nächsten Verschiebung weitergegeben, ohne dass zusätzliche Instruktionen notwendig sind.

Verschiebeoperatoren in C, C++ und Java

In C, C++ und verwandten Sprachen werden die Verschiebungsoperatoren durch „<<“ und „>>“ dargestellt. Die Anzahl der Verschiebungen wird als zweiter Operand übergeben. Beispiel:

x = y << 2

weist der Variable x das Ergebnis der bitweisen Verschiebung von y um zwei Stellen nach links zu. Dies führt zum selben Ergebnis wie x = y * 4.

In C und C++ verwenden Berechnungen mit vorzeichenlosen Werten logische Verschiebungen; Berechnungen mit vorzeichenbehafteten Werten sind undefiniert, sofern der rechte Operand negativ ist, durch einen Linksshift sich das Vorzeichen ändert oder ein negativer Wert einem Rechtsshift unterzogen wird.^[1]

In Java sind alle Ganzzahl-Datentypen vorzeichenbehaftet, und die Operatoren „<<“ und „>>“ führen arithmetische Verschiebungen durch. In Java gibt es zusätzlich den Operator „>>>“, der eine logische Rechtsverschiebung durchführt. Da logische und arithmetische Linksverschiebungen identisch sind, gibt es keinen „<<<“ Operator.

Anwendungen

Obwohl Rechner oft effiziente Befehle zur Ausführung von arithmetischen und logischen Operationen eingebaut haben, können alle diese Operationen auch durch Kombinationen von bitweisen Operatoren und Nullvergleichen durchgeführt werden. Folgender Pseudocode zeigt beispielsweise, wie zwei beliebige Ganzzahlen a und b nur mithilfe von Verschiebungen und Additionen multipliziert werden können:

c := 0
solange b ≠ 0
    falls (b und 1) ≠ 0
        c := c + a
    schiebe a um 1 nach links
    schiebe b um 1 nach rechts
return c

Siehe auch

• Boolesche Algebra
• Boolescher Operator
• Logikgatter
• Logischer Operator

Quellen

1. ↑ ISO/IEC-Standard „C programming language“, Abschnitt 6.5.7#5 (englisch)

Weblinks

• Division durch bitweise Verschiebung (englisch)