- Borelmass
-
Als Borelmaß (nach Émile Borel) bezeichnet man im mathematischen Gebiet der Maßtheorie diejenigen Maße µ auf der Borelschen σ-Algebra eines Hausdorff-Raums X, für die gilt:
Diese Eigenschaft bezeichnet man als lokale Endlichkeit[1]. Wenn der Raum X lokal-kompakt ist, entspricht lokale Endlichkeit der Forderung, dass µ auf kompakten Mengen endlich ist.
Ein Spezialfall ist das Lebesgue-Borel-Maß.
Weitere Bedeutungen
Der Begriff wird in der Fachliteratur nicht einheitlich verwendet. Manchmal werden auch
- äußere Maße, bezüglich derer alle Borelmengen messbar sind[2]
- Das Maß auf der borelschen σ-Algebra auf
 , das jedem Intervall [a,b] das Maß b − a zuordnet
, das jedem Intervall [a,b] das Maß b − a zuordnet
als Borelmaß bezeichnet.
Einzelnachweise
Wikimedia Foundation.


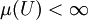 .
.