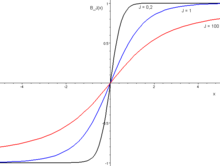
- Brillouin-Funktion
-
Die Brillouin-Funktion ist eine spezielle Funktion, die aus der quantenmechanischen Beschreibung eines Paramagneten hervorgeht. Benannt ist sie nach dem französisch-amerikanischen Physiker Léon Brillouin. Die Definition der Brillouin-Funktion lautet:
Dabei bezeichnet J in der Anwendung in der Physik die Gesamtdrehimpulsquantenzahl. Bei der Beschreibung eines Paramagneten ist es sinnvoll den Parameter ξ einzuführen, welcher wie folgt definiert ist:
Die einzelnen Formelzeichen stehen für folgende Größen:
- m – Magnetisches Moment eines Teilchens
- B – Betrag des angelegten äußeren Magnetfeldes
- kB – Boltzmann-Konstante
- T – Absolute Temperatur
- g – Landé-Faktor
- μB – Bohrsches Magneton
Mit dem Parameter ξ kann nun die Magnetisierung M eines Paramagneten mit der Stoffmenge N in einem äußeren Magnetfeld formuliert werden:
Eine weitere, halb-klassische Beschreibung eines Paramagneten geschieht mit Hilfe der Langevin-Funktion:
Diese ergibt sich im Limes
 und zugleich
und zugleich  (wobei das magnetische Gesamtmoment konstant bleibt) aus der Brillouin-Funktion.
(wobei das magnetische Gesamtmoment konstant bleibt) aus der Brillouin-Funktion.Siehe auch: Langevin-Funktion.
Literatur
- Torsten Fließbach: Statistische Physik – Lehrbuch zur Theoretischen Physik IV. Elsevier-Spektrum Akademischer Verlag, Heidelberg 2006.
Weblinks
Wikimedia Foundation.