Reziproke Proportionalität

Reziproke Proportionalität^[1], indirekte bzw. umgekehrte Proportionalität^[2] oder Antiproportionalität besteht zwischen zwei Größen, deren Produkt konstant ist. Die eine Größe ist dann eine reziprok proportionale (auch: antiproportionale) Funktion der anderen Größe. Die Verdopplung (Verdreifachung, Halbierung, ...) der einen ist mit einer Halbierung (Drittelung, Verdopplung, ...) der anderen verbunden. Der Funktionsgraph ist eine Hyperbel, die sich den Koordinatenachsen asymptotisch annähert.

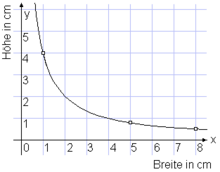
Funktionsgraph eines reziprok proportionalen Zusammenhangs: Höhe und Breite von Rechtecken mit Flächeninhalt A = 4 cm²

In Anwendungen ist das konstante Produkt bekannt oder wird aus einem gegebenen Wertepaar (x₀, y₀) berechnet. Danach kann man die eine Größe (y) als Funktion der anderen (x) ausrechnen:

$y = \frac{A}{x} = \frac{x_0 y_0}{x}$.

Beispiel: Gegeben ist ein Rechteck, 8 cm breit und 0,5 cm hoch. Gesucht ist ein flächengleiches Rechteck der Breite 5 cm.

Die konstante Fläche ist A = 8 cm · 0,5 cm = 4 cm². Die gesuchte Höhe ist A/5 cm = 0,8 cm.

Nebenstehendes Diagramm zeigt die beiden Wertepaare als markierte Punkte. An der Hyperbel y = A/x kann man weitere flächengleiche Rechtecke ablesen, z.B. 1 cm breit, 4 cm hoch.

Schreibweise

Für „a ist umgekehrt proportional zu b“ schreibt man kurz:   $a \sim \frac{1}{b}$

Einzelnachweise

1. ↑ So im Bronstein benannt
2. ↑ Das große Tafelwerk interaktiv ISBN 978-3-464-57143-9