Diskrete Menge

Diskretheit (lat. discretus „unterschieden“, „getrennt“) bezeichnet allgemein eine räumliche oder zeitliche Trennung von Objekten oder Ereignissen.

Ein diskretes Signal besteht aus zeitlich oder räumlich getrennten Teilen, zum Beispiel sind Rauchzeichen und Morsezeichen diskret. Zu unterscheiden ist das Signal vom Signalträger, der bei der elektrischen Übertragung von Morsezeichen ein kontinuierlicher elektrischer Strom ist.

Diskrete Signale sind seit der Erfindung des Computers meist auch binär, d. h. sie bestehen aus einer Abfolge von zwei verschiedenen Werten, etwa 0 und 1.

Diskretheit in der Mathematik

Diskrete Teilmengen der reellen Zahlen

In der Mathematik wird eine Teilmenge M der reellen Zahlen als diskrete Teilmenge bezeichnet, wenn es zu jedem Element 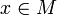$x \in M$ ein offenes Intervall gibt, das außer x kein weiteres Element von M enthält. Die Elemente einer diskreten Menge sind anschaulich voneinander isoliert, getrennt.

Zum Beispiel ist die Menge der ganzen Zahlen eine diskrete Teilmenge der reellen Zahlen. Die rationalen Zahlen sind dagegen nicht diskret, denn z. B. für die Zahl 0 gibt es kein offenes Intervall, das außer 0 keine weiteren Brüche enthält.

Diskretheit bedeutet nicht, dass es zwischen je zwei Elementen einer diskreten Menge nur endlich viele Elemente geben muss. Zum Beispiel ist die Menge 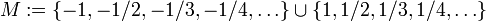$M := \{-1, -1/2, -1/3, -1/4, \ldots\} \cup \{1, 1/2, 1/3, 1/4, \ldots \}$ eine diskrete Teilmenge: Für jedes Element 1 / n gibt es das offene Intervall ]1 / (n + 1),1 / (n − 1)[, das aus M nur 1 / n enthält; analoges gilt für die Elemente − 1 / n. Zwischen -1 und 1 liegen jedoch unendlich viele Elemente von M. In einem bestimmten Sinn ist Diskretheit das Gegenteil zu Kontinuität.

Diskrete Teilmengen in höheren Dimensionen

Analog bezeichnet man 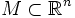$M \subset \mathbb R^n$ als diskret, wenn für alle 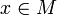$x \in M$ eine offene Umgebung in 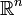$\mathbb R^n$ existiert, die außer x kein weiteres Element von M enthält. Äquivalent ist die Forderung, dass M keinen Häufungspunkt enthält.

Diskrete Teilmenge eines topologischen Raums

Man verallgemeinert den Begriff des isolierten Punktes auf topologische Räume durch folgende Definition:

Ein Punkt x des topologischen Raumes X heißt isolierter Punkt, wenn die einelementige Menge {x} offen ist.

Ein isolierter Punkt hat also eine Umgebung, "in der er allein ist". Mit diesem Begriff verallgemeinert man nun den Begriff der diskreten Teilmenge:

Ein topologischer Raum heißt diskreter topologischer Raum, wenn jeder seiner Punkte isoliert ist.

Eigenschaften

In einem diskreten topologischen Raum ist jede Teilmenge offen.

Eine Funktion von einem topologischen Raum, deren Bildmenge diskret ist, ist genau dann stetig, wenn sie lokal konstant ist.

Jede Funktion, deren Definitionsbereich diskret ist, ist stetig.

Diskreter metrischer Raum

Ein metrischer Raum, dessen Metrik die Gestalt d(x, y) = 1 für x ≠ y hat, heißt diskreter metrischer Raum.

Eigenschaften

Ein diskreter metrischer Raum ist vollständig und auch als topologischer Raum diskret.

Ein metrischer Raum, der als topologischer Raum diskret ist, muss allerdings nicht die diskrete Metrik besitzen, und auch nicht vollständig sein. Zum Beispiel ist die im Abschnitt "Diskrete Teilmenge der reellen Zahlen" angegebene Menge M = {-1/n, 1/n | n in N} ein diskreter topologischer Raum, aber der Grenzwert 0 der Cauchyfolge (1, 1/2, 1/3, ...) liegt außerhalb von M.

Siehe auch

• Abzählbarkeit