Kernel-Regression

Unter Kernel-Regression versteht man eine Reihe nichtparametrischer statistischer Methoden, bei denen die Abhängigkeit einer zufälligen Größe von Ausgangsdaten mittels Kerndichteschätzung geschätzt werden. Die Art der Abhängigkeit, dargestellt durch die Regressionskurve, wird im Gegensatz zur linearen Regression nicht als linear festgelegt. Der Vorteil ist eine bessere Anpassung an die Daten im Falle nichtlinearer Zusammenhänge. Abhängig davon, ob die Ausgangsdaten selbst zufällig sind oder nicht, unterscheidet man zwischen Random-Design- und Fixed-Design-Ansätzen. Das grundlegende Verfahren wurde 1964 unabhängig voneinander von Geoffrey Watson und Elisbar Nadaraia (englische Transkription: Elizbar Nadaraya) vorgeschlagen.

Univariate Kernel-Regression

Kerndichteschätzer

Dotplot, Histogramm und Kerndichteschätzer der Variablen LSTAT des Boston Housing Datensatzes.

Ein Kerndichteschätzer $\hat{f}$ zur Bandweite h > 0 ist eine Schätzung der unbekannten Dichtefunktion f einer Variablen. Ist $x_1,\ldots,x_n$ eine Stichprobe, K ein Kern, so ist die Kerndichteschätzung definiert als:

$\hat{f}(x)=\frac{1}{n}\sum_{j=1}^{n}K_h(x-x_j)=\frac{1}{nh}\sum_{j=1}^{n}K\left(\frac{x-x_j}{h}\right)$.

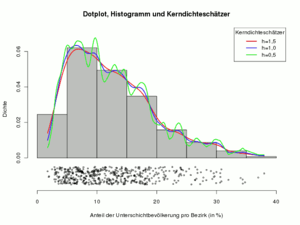
Wie die Grafik rechts zeigt, ist die Wahl der Bandbreite h entscheidend für die Qualität der Approximation.

→ Hauptartikel: Kerndichteschätzer

Typische Kerne mit
unbeschränktem Träger		Träger [ − 1;1]
Kern	$K(u)\,$	Kern	$K(u) I(|u|\le 1)$
Gauß	$\tfrac{1}{\sqrt{2\pi}} \exp(-\tfrac{1}{2}u^2)$	Uniform	$\tfrac{1}{2}$
Cauchy	$\tfrac{1}{\pi(1+u^2)}$	Dreieck	(1 − | u | )
Picard	$\tfrac{1}{2}\exp(-|u|)$	Kosinus	$\tfrac{\pi}{4}\cos(\tfrac{\pi}{2}u)$
		Epanechnikov (p=1) Quartic (p=2) Triweight (p=3)	Cp(1 − u2)p Cp = 3 / 4 Cp = 15 / 16 Cp = 35 / 32

Nadaraya-Watson-Schätzer

Lineare Regression (schwarz) und Nadaraya-Watson-Schätzer mit verschiedenen Bandweiten (rot: mittel, grün: groß und blau: klein)

Der Nadaraya-Watson-Schätzer schätzt eine unbekannte Regressionsfunktion m(x) aus den Beobachtungsdaten (x₁,y₁),...,(x_n,y_n) als ^[1][2]

$\hat{m}(x)=\frac{\sum_{i=1}^n y_i K_h(x-x_i)}{\sum_{i=1}^n K_h(x-x_i)}$

mit K_h(u) = 1 / hK(u / h) und einem Kern K und einer Bandweite h > 0. Die Funktion K_h ist dabei eine Funktion, die Beobachtungen nahe x ein großes Gewicht und Beobachtungen weit entfernt von x ein kleines Gewicht zuordnet. Die Bandweite legt fest, in welchem Bereich um x die Beobachtungen ein großes Gewicht haben.

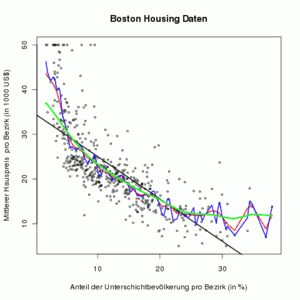
Während die Wahl des Kerns meist recht frei erfolgen kann, hat die Wahl der Bandweite einen großen Einfluss auf die Glattheit des Schätzers. Die Grafik rechts zeigt, dass eine große Bandweite (grün) zu einer glatteren Schätzung führt als die Wahl einer kleinen Bandweite (blau).

Ableitung

Die Idee des Nadaraya-Watson-Schätzers beruht darauf, dass die unbekannte Regressionsfunktion

Y = m(X)

mit Hilfe des bedingten Erwartungswertes durch die gemeinsame Dichte f(x,y) und die Randdichte f_X(x) dargestellt wird.

$m(x)=E(Y|X=x) = \int y \frac{f(x,y)}{f_X(x)} dy = \frac{\int f(x,y) dy}{f_X(x)}$

Die unbekannten Dichten f(x,y) und f_X(x) werden mit Hilfe einer Kerndichteschätzung geschätzt. Zur Berechnung der gemeinsamen Dichte aus den Beobachtungen wird ein bivariater Kerndichteschätzer mit Produktkern K(x,y) = K(x)K(y) und Bandweiten g und h genutzt:

$\hat{f}_{g,h}(x,y)=\frac{1}{n}\sum_{i=1}^n K_h(x-x_i)K_g(y-y_i)$.

Es folgt

$\int y \left(\frac{x-x_i}{h}\right) dy = \frac{1}{n}\sum_{i=1}^n y_i K_h(x-x_i)$

und mittels Kerndichteschätzung für f_X(x) der Nadaraya-Watson-Schätzer.

Eigenschaften

Gewichte W_hi(x) für verschiedene x, i und Bandweiten h.

1. Wie im Fall der linearen Regression kann der Nadaraya-Watson-Schätzer auch als Linearkombination der y_i mit Gewichtsfunktionen W_hi geschrieben werden:

$\hat{m}(x)=\sum_{i=1}^n y_i W_{hi}(x)$.

Damit ist der Nadaraya-Watson-Schätzer das (lokal) gewichtete Mittel der Beobachtungswerte y_i, es gilt

$\tfrac{1}{n}\sum_{i=1}^n W_{hi}(x)=1$.

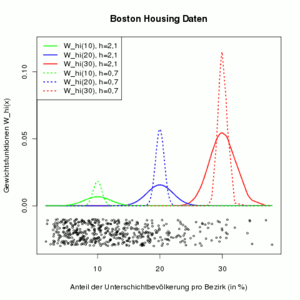
Die Grafik rechts zeigt die Gewichte für verschiedene Werte von x (blau: x = 10, grün: x = 20, rot: x = 30). Der Dotplot unterhalb von Null zeigt die Daten der erklärenden Variable. Je größer die Bandweite ist (durchgezogene Linie vs. gestrichelte Linie), desto mehr Beobachtungen um x haben ein Gewicht ungleich Null. Je weniger Daten zu Verfügung stehen (rechts), desto stärker müssen die verfügbaren Beobachtungen gewichtet werden.

2. Die mittlere quadratische Abweichung ergibt sich approximativ als

$MSE(\hat{m}(x))\approx \underbrace{h^4 B^2}_{Bias^2} + \underbrace{\tfrac{1}{nh}V}_{Varianz}$

mit B und V unabhängig von n und h. Damit ist die Konvergenz langsamer als bei der linearen Regression, d.h. mit der gleichen Zahl von Beobachtungen kann der Vorhersagewert in der linearen Regression präziser geschätzt werden als beim Nadaraya-Watson-Schätzer.

Dabei ist die Verzerrung des Nadaraya-Watson-Schätzers

$Bias^2(\hat{m}(x)) = \frac{h^4}{4}\left(m''(x)+2\frac{m'(x)f'_X(x)}{f_X(x)} \mu_2^2(K) \right)$

mit m'(x) und m''(x) die erste bzw. zweite Ableitung der unbekannten Regressionsfunktion, f'_X(x) die erste Ableitung der Dichte f_X(x) und $\mu_2(K) = \int u^2 K(u) du$.

Und die Varianz des Schätzers

$Var(\hat{m}(x)) = \frac{1}{nh}\frac{\sigma^2(x)}{f_X(x)}|K|_2^2$

mit σ²(x) = Var(Y | X = x) und $|K|_2 = \int K^2 (u)du$.

Bandweitenwahl

Resubstitution und Leave-One-Out Kreuzvalidierung für die Bandweite des Nadaraya-Watson Schätzers für das obige Beispiel. Die "optimale" Bandweite ergibt sich für ca. h = 0,7.

Das Hauptproblem bei der Kernel-Regression ist die Wahl einer geeigneten Bandweite h. Als Basis dient die Minimierung der mittlere quadratische Abweichung

$MSE(\hat{m}(x))=E\left((\hat{m}(x)-m(x))^2\right)$

bzw. deren Approximation. Die Approximation enthält jedoch die zweite Ableitung der unbekannten Regressionsfunktion m''(x) sowie die unbekannte Dichtefunktion f_X(x) und deren Ableitung. Stattdessen wird die datenbasierten gemittelte quadratische Abweichung

$ASE(\hat{m}(x))=\frac{1}{n}\sum_{i=1}^n (\hat{m}(x)-y_i)^2$

minimiert. Da zur Schätzung von $\hat{m}(x)$ der Wert von y_i genutzt wird, führt eine Bandweite h = 0 zu einem $ASE(\hat{m}(x))=0$ (Resubstitution Schätzung). Daher wird eine Leave-One-Out-Kreuzvalidierung durchgeführt, d.h. zur Berechnung des Schätzwertes $\hat{m}(x_i)$ werden alle Beobachtungen herangezogen außer der i-ten. Damit wird der $ASE(\hat{m}(x))$ für verschiedene Bandweiten berechnet. Die Bandweite, die einen minimalen ASE ergibt wird dann zur Schätzung der unbekannten Regressionfunktion genommen.

Konfidenzbänder

Nach der Schätzung der Regressionsfunktion $\hat{m}(x)$ stellt sich die Frage, wie weit diese von der wahren Funktion m(x) abweicht. Die Arbeit von Bickel und Rosenblatt (1973)^[3] liefert zwei Theoreme für punktweise Konfidenzbänder und gleichmässige Konfidenzbänder.

Neben der Information über die Abweichung zwischen $\hat{m}(x)$ und m(x) liefern die Konfidenzbänder einen Hinweis darauf, ob ein mögliches parametrisches Regressionsmodell, z.B. eine lineare Regression, zu den Daten passt. Liegt der geschätzte Verlauf der Regressionfunktion des parametrisches Regressionsmodell außerhalb der Konfidenzbänder, so ist dies ein Hinweis darauf, dass das parametrische Regressionsmodell nicht zu den Daten passt. Ein formaler Test ist mit Hilfe von Bootstrap-Verfahren möglich.

Lineare Regression (schwarz) und Nadaraya-Watson-Schätzer (rot) mit optimaler Bandweite und punktweisen 95%-Konfidenzband.

Punktweise Konfidenzbänder: Unter bestimmten Voraussetzungen konvergiert in Verteilung

$n^{2/5}\left(\hat{m}(x)-m(x)\right)\longrightarrow N(B(x), V(x))$

mit h = cn^{1 / 5}, $B(x) = c\mu_2(K)\left(\tfrac{m''(x)}{2}+\tfrac{m'(x)f'_X(x)}{f_X(x)}\right)$ und $V(x) = \tfrac{\sigma(x)|K|^2_2}{cf_X(x)}$.

Wenn die Bandweite klein genug ist, dann kann der asymptotische Bias B(x) vernachlässigt werden gegen die asymptotische Varianz V(x). Damit können approximative 1 − α Konfidenzbänder berechnet werden

$\hat{m}(x)\pm z_{1-\alpha/2} \sqrt{\tfrac{|K|_2^2 \hat{\sigma}^2(x)}{nh\hat{f}_X(x)}}$

mit z_{1 − α / 2} das 1 − α / 2 Quantil der Standardnormalverteilung. Die unbekannte Dichte f_x(x) wird dabei mit einer Kerndichteschätzung $\hat{f}_X(x)$ geschätzt und σ²(x) mit

$\hat{\sigma}^2(x) = \tfrac1n \sum_{i=1}^n W_{hi}(x) \left(y_i-\hat{m}(x)\right)^2$.

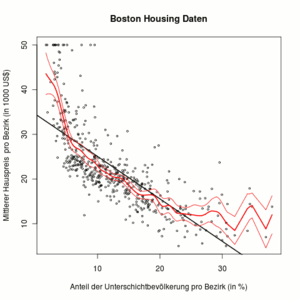
Die Grafik rechts zeigt den Nadaraya-Watson Schätzer mit punktweisen 95% Konfidenzband (rote Linien). Die schwarze lineare Regressionsgerade liegt in verschiedenen Bereichen deutlich außerhalb der Konfidenzbandes. Dies ist ein Hinweis darauf, dass ein lineares Regressionsmodell hier nicht angemessen ist.

Gleichmässige Konfidenzbänder: Unter etwas stärkeren Voraussetzungen als zuvor und mit $x\in[0;1]$, h = n ^{− κ} mit 1 / 5 < κ < 1 / 2 und für Kerne mit Träger in [ − 1;1] konvergiert

$P\left(|\hat{m}(x)-m(x)|\leq z_{n,\alpha} \sqrt{\tfrac{|K|_2^2 \hat{\sigma}^2(x)}{nh\hat{f}_X(x)}}\right) \longrightarrow 1-\alpha$

mit

$z_{n,\alpha}=\sqrt{ \tfrac{1}{\sqrt{2\kappa\log(n)}}\left(\log\left(\tfrac{1}{2\pi}\tfrac{|K'|_2}{|K|_2}\right)^{1/2}-\log\left(-\tfrac12\log(1-\alpha)\right)\right)+ \sqrt{2\kappa\log(n)}}$.

Die Bedingung $x\in[0;1]$ ist keine Einschränkung, da die Daten x_i erst auf das Intervall [0;1] transformiert werden können. Danach wird das Konfidenzband berechnet und wieder zurücktransformiert auf die Originaldaten.

Gasser-Müller-Schätzer

Im Fixed-Design-Fall mit $a=x_1\leq x_2\leq ... \leq x_n=b$ ist die Dichte f_X(x) bekannt, muss also nicht geschätzt werden. Dies vereinfacht sowohl die Berechnungen als auch die mathematische Behandlung des Schätzers. Für diesen Fall wurde der Gasser-Müller-Schätzer definiert als^[4]

$\hat{m}^{GM}(x)=\sum_{i=1}^n y_i W_{hi}^{GM}(x)$

mit

$W_{hi}^{GM}(x)=n \int_{s_{i-1}}^{s_i} K_h(x-u) du$

und s₀ = a, s_{n + 1} = b und s_i = (x_i + x_{i − 1}) / 2.

Eigenschaften

1. Der Gasser-Müller Schätzer ist wie der Nadaraya-Watson-Schätzer ein linearer Schätzer und die Summe der Gewichtsfunktionen ist Eins.

2. Für die mittlere quadratische Abweichung gilt:

$MSE(\hat{m}^{GM}(x)) \approx \underbrace{\tfrac{h^4}{4} \mu_2^2(K) (m''(x))^2}_{Bias^2} + \underbrace{\tfrac{1}{nh}\|K\|^2_2}_{Varianz}$.

Lokal polynomiale Kernel-Regression

Lokale Approximationen für den Nadaraya-Watson-Schätzer (lokal konstant) und den lokal linearen Schätzer an ausgewählten Datenpunkten. Die Grafik ist eingeschränkt auf Bereich [1.5;5] der x-Werte (also linker Rand der Daten), die Berechnungen wurden jedoch mit allen Daten durchgeführt.

Der Nadaraya-Watson Schätzer kann als Lösung des folgenden lokalen Minimierungsproblem geschrieben werden:

$\min_{\beta_0^{(0)}} \sum_{i=1}^n \left(y_i -\beta_0^{(0)}\right)^2 K_h(x-x_i)$,

d.h. für jedes x wird ein lokal konstanter Wert $\beta_0^{(0)}$ bestimmt, der gleich dem Wert des Nadaraya-Watson Schätzer $\hat{m}(x)$ an der Stelle x ist.

Anstelle einer lokalen Konstanten kann auch ein Polynom verwendet werden:

$\min_{\beta_0^{(p)},...,\beta_p^{(p)}} \sum_{i=1}^n (y_i -\beta_0^{(p)}-\beta_1^{(p)} (x_i-x) - ... -\beta_p^{(p)} (x_i-x)^p)^2 K_h(x-x_i)$,

d.h. der unbekannten Regressionswert wird durch eine lokales Polynom approximiert. Die lokal polynomiale Kernel-Regression m_p(x) ergibt sich an jeder Stelle durch

$m_p(x)=\hat{\beta}_0^{(p)}$.

Die Grafik rechts zeigt an ausgewählten Stellen x die verwendeten lokalen Polynome. Der Nadaraya-Watson Schätzer (rot) nutzt lokal konstanten Funktionen $\beta_0^{(0)}$. Die lokal lineare Kernel-Regression (blau) nutzt lokal lineare Funktionen $\beta_0^{(1)}+\beta_1^{(1)} (\tilde{x}-x)$ an der Stelle x. Die ausgewählten Stellen x sind in der Grafik mit Datenpunkten identisch. Die senkrechten grauen Linien verbinden die lokalen Polynome mit dem zugehörigen x-Wert (Datenpunkt). Der Schnittpunkt mit dem roten bzw. blauen Polynom ergibt den Schätzwert an der entsprechenden Stelle x für den Nadaraya-Watson Schätzer und die lokal lineare Kernel-Regression.

Vorteile und Eigenschaften

Die lokal polynomiale Regression bietet gegenüber dem Nadaraya-Watson Schätzer einige Vorteile:

• Im allgemeinen wird das lokal konstante $\beta_0^{(0)}$ von Beobachtungswerten beeinflusst die sowohl links als auch rechts vom Wert x liegen. An den Rändern funktioniert das jedoch nicht und dies führt zu boundary effects. Die lokal polynomiale Kernel-Regression approximiert jedoch lokal mit einem Polynom und kann dieses Problem vermeiden.
• Um die vte Ableitung zu schätzen, könnte man einfach den Nadaraya-Watson entsprechend oft ableiten. Mit der lokal polynomialen Kernel-Regression ergibt sich jedoch ein deutlich eleganterer Weg:

$m_p^{(v)}(x)=v!\hat{\beta}_v^{(p)}$

Meist wird p = v + 1 oder p = v + 3 benutzt. Ungerade Ordnungen p sind besser als gerade Ordnungen.

• Wie im Fall der linearen Regression und des Nadaraya-Watson-Schätzer kann auch die lokal polynomiale Kernel-Regression auch als Linearkombination der y_i mit Gewichtsfunktionen $W_{hi}^{(p)}$ geschrieben werden:

$\hat{m}_p(x)=\sum_{i=1}^n y_i W_{hi}^{(p)}(x)$.

Schätzung der Beta-Koeffizienten

Definiert man die folgenden Matrizen:

$\mathcal{X}=\begin{pmatrix} 1 & (x_1-x) & \cdots & (x_1-x)^p \\ 1 & (x_2-x) & \cdots & (x_2-x)^p \\ \vdots & \vdots & & \vdots \\ 1 & (x_n-x) & \cdots & (x_n-x)^p \end{pmatrix}$, $\mathcal{Y}=\begin{pmatrix} y_1\\ y_2 \\ \vdots\\ y_n \end{pmatrix}$

und

$\mathcal{W}=\begin{pmatrix} K_h(x-x_1) & 0 & \cdots & 0\\ 0 & K_h(x-x_2) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & K_h(x-x_n) \end{pmatrix}$

so ergeben sich die Schätzung der Beta-Koffizienten $\beta=(\beta_0^{(p)}, ..., \beta_p^{(p)})$ als

$\hat{\beta} = \left(\mathcal{X}^T\mathcal{W}\mathcal{X}\right)^{-1}\mathcal{X}^T\mathcal{W}\mathcal{Y}$.

Die für die Ableitung notwendigen Koeffizienten werden im Schätzverfahren also automatisch mit berechnet!

Um die Schätzung praktisch durchzuführen, berechnet man

$S_j = \sum_{i=1}^n K_h(x-x_i) (x_i-x)^j$

$T_j = \sum_{i=1}^n K_h(x-x_i) (x_i-x)^j y_i$

und berechnet

$\hat{\beta}=\begin{pmatrix} S_0 & S_1 & \cdots & S_p\\ S_1 & S_2 & \cdots & S_{p+1} \\ \vdots & \vdots & \ddots & \vdots \\ S_p & S_{p+1} & \cdots & S_{2p} \end{pmatrix}^{-1}\begin{pmatrix} T_0\\ T_1 \\ \vdots\\ T_p \end{pmatrix}$

Lokal lineare Kernel-Regression

Verschiedene lokale Regressionsmethoden: Nadaraya-Watson (rot), Lokal-linear (blau) und LOWESS (grün) und lineare Regression (schwarz).

Einer der bekannteste lokal linearen Regressionsmodelle (p = 1) ist der LOESS oder LOWESS (engl. Abkürzung von locally weighted scatterplot smoothing).^[5] Der LOWESS ist jedoch keine lokal-lineare Kernel-Regression, denn

• die Regressionsgewichte werden robust geschätzt und
• die Bandweite variiert mit x.

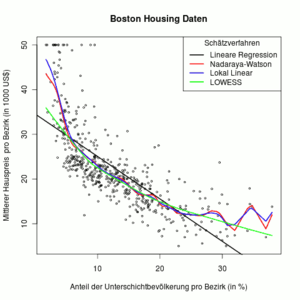
Die Grafik rechts zeigt zwei verschiedene Methoden der Kernel-Regression: Lokal konstant (rot, Nadaraya-Watson) und lokal linear (blau). Insbesondere an den Rändern approximiert die lokal lineare Kernel-Regression die Daten etwas besser.

Die lokal lineare Kernel-Regression ergibt sich als

$\hat{m}_1(x)=\tfrac{T_0S_2-T_1S_1}{S_0S_2-S_1 2}$.

Der mittlere quadratische Fehler der lokal linearen Regression ergibt sich, wie beim Nadaraya-Watson-Schätzer, als

$MSE(\hat{m}_1(x))\approx \underbrace{h^4 B^2}_{Bias^2} + \underbrace{\tfrac{1}{nh}V}_{Varianz}$

mit

$Bias^2(\hat{m}_1(x)) = \frac{h^4}{4}\left(m''(x)\right)^2 \mu_2^2(K)$

und die Varianz ist identisch zur Varianz des Nadaraya-Watson-Schätzers $Var(\hat{m}(x))$. Die einfachere Form des Bias macht die lokal linearen Kernel-Regression attraktiver für praktische Zwecke.

Einzelnachweise

1. ↑ Elizbar A. Nadaraya: On estimating regression. In: Theory of Probability and its Applications. 9, Nr. 1, 1964, S. 141-142, doi:10.1137/1109020.
2. ↑ Geoffrey S. Watson: Smooth Regression Analysis. In: Sankhyā: The Indian Journal of Statistics, Series A. 26, Nr. 4, Dezember 1964, S. 359-372.
3. ↑ Bickel, Rosenblatt (1973) On some global measures of the deviations of density function estimators, Annals of Statistics 1, S. 1071-1095
4. ↑ Theo Gasser, Hans-Georg Müller: Estimating Regression Functions and Their Derivatives by the Kernel Method. In: Scandinavian Journal of Statistics. 11, Nr. 3, 1984, S. 171-185.
5. ↑ W.S. Cleveland: Robust Locally Weighted Regression and Smoothing Scatterplots. In: Journal of the American Statistical Association. 74, Nr. 368, Dezember 1979, S. 829-836 (http://jstor.org/stable/2286407).

Literatur

• Jianqing Fan, Irene Gijbels: Local Polynomial Modelling and Its Applications. Chapman and Hall/CRC, 1996, ISBN 978-0412983214.
• Wolfgang Härdle, Marlene Müller, Stefan Sperlich, Axel Werwatz: Nonparametric and Semiparametric Models. Springer Verlag, Berlin, Heidelberg 2004, ISBN 978-3540207221 (http://fedc.wiwi.hu-berlin.de/xplore/ebooks/html/spm).
• Tristen Hayfield, Jeffrey S. Racine: Nonparametric Econometrics: The np Package. In: Journal of Statistical Software. 27, Nr. 5, 2008 (http://www.jstatsoft.org/v27/i05/).
• M.P. Wand, M.C. Jones: Kernel Smoothing. Chapman and Hall/CRC, 1994, ISBN 978-0412552700.