Charakteristische Funktion (Physik)

Die charakteristischen Funktionen (auch charakteristische Potentialformen genannt) bezeichnen in der Thermodynamik die totalen Differentiale und damit die Änderungen der thermodynamischen Potentiale: Innere Energie U, Enthalpie H, Freie Energie F, Freie Enthalpie G sowie Großkanonisches Potential Ω.

Die wichtigste charakteristische Funktion ist die aus dem Ersten und Zweiten Hauptsatz der Thermodynamik folgende Fundamentalgleichung

$\mathrm dU(S;V;N) = T dS - p dV + \mu {d}N. \!$

Die (kursiv geschriebenen) Differentiale auf der rechten Seite sind allesamt extensiv und haben die bekannte Bedeutung, z. B. ist S die Entropie. Das (nicht-kursiv geschriebene) Differential auf der linken Seite ist ein sog. totales Differential, verschwindet also bei Integration über einen geschlossenen Weg.

Aus der Definition der Enthalpie H

$H(S;p;N) = U(S;V;N) + pV \!$

folgt wegen $d(pV) = p dV + V dp \!$:

$\mathrm dH = \mathrm dU(S;V;N) + p dV + V dp, \!$

und mit der Fundamentalgleichung erhält man

$\mathrm dH(S;p;N) = T dS - p dV + \mu {d}N + p dV + V dp \!$

und damit die charakteristische Funktion:

$\mathrm dH(S;p;N) = T dS + V dp + \mu {d}N. \!$

Hier ist das zweite Differential auf der rechten Seite intensiv. Das Differential auf der linken Seite ist erneut total.

Aus der Definition der Freien Enthalpie G

$G(T;p;N) = H(S;p;N) - TS \!$

folgt ferner

$\mathrm dG(T;p;N) = \mathrm dH(S;p;N) - TdS - S dT, \!$

und damit die charakteristische Funktion

$\mathrm dG(T;p;N) = - S dT + V dp + \mu {d}N. \!$

Zuletzt noch die Definitionen der Freien Energie F und des sog. Großkanonischen Potentials Ω:

$F(T;V;N) = U(S;V;N) - TS \!$ und

$\Omega(T;V;\mu) =F(T;V;N)-\mu N\,.$

Es folgen entsprechend

$\mathrm dF(T;V;N) = -S dT - p dV + \mu {d}N \!$ und

$\mathrm d\Omega(T;V;\mu)= -S{d}T - p{d}V- N{d}\mu\,.$

Guggenheim-Schema

Guggenheim-Quadrat

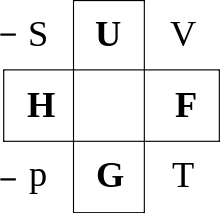
Zum praktischen Arbeiten kann man das sogenannte Guggenheim-Quadrat benutzen. Hieraus erhält man alle oben genannten charakteristischen Funktionen bis auf die des Großkanonischen Potentials, welche aber sehr ähnlich der der Freien Energie ist.

Man findet die Relation indem man das totale Differential aus der Mitte einer der vier Seiten des Schemas entnimmt und dann aus den gegenüberliegenden Ecken sowie den zwei benachbarten Feldern die rechte Seite abliest. Am Ende muss man stets den Summanden μdN hinzufügen.

Zum Beispiel entnimmt man U aus der oberen Seite, woraus das totale Differential dU der linken Seite der Gleichung folgt. Schräg gegenüber liegt dann beispielsweise T und von diesem wiederum diagonal gegenüber S, was zum Ausdruck TdS führt. Analog erhält man den Summanden − pdV mit der Besonderheit, dass wenn der Koeffizient des Summanden auf der linken Seite des Quadrats liegt, ein negatives Vorzeichen vorangestellt wird. Dies gilt jedoch nur für Koeffizienten. Es ergibt sich damit wie oben erwähnt dU = TdS − pdV + μdN.

Merksprüche für das Quadrat finden sich unter: Guggenheim-Quadrat (Merksprüche)

Siehe auch

• totales Differential