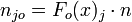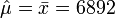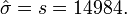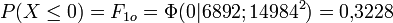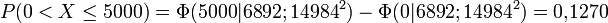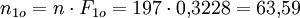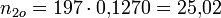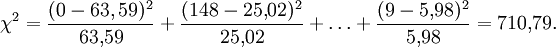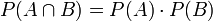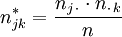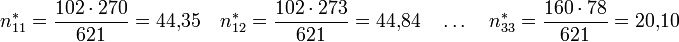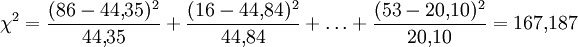Chi-Quadrat-Anpassungstest

Mit dem χ²-Test (Chi-Quadrat-Test) untersucht man Verteilungseigenschaften einer statistischen Grundgesamtheit.

Man unterscheidet vor allem die beiden Tests:

• Verteilungstest oder Anpassungstest: Hier wird geprüft, ob vorliegende Daten auf eine bestimmte Weise verteilt sind.
• Unabhängigkeitstest: Hier wird geprüft, ob zwei Merkmale stochastisch unabhängig sind.

Verteilungstest

Man betrachtet ein statistisches Merkmal x, dessen Wahrscheinlichkeiten in der Grundgesamtheit unbekannt sind. Es wird bezüglich der Wahrscheinlichkeiten von x eine vorläufig allgemein formulierte Nullhypothese

H₀: Das Merkmal x hat die Wahrscheinlichkeitsverteilung F_o(x)

aufgestellt.

Vorgehensweise

Die n Beobachtungen von x liegen in m verschiedenen Kategorien j (j = 1, …, m) vor. Treten bei einem Merkmal sehr viele Ausprägungen auf, fasst man sie zweckmäßigerweise in m Klassen zusammen und fasst die Klassenzugehörigkeit als j-te Kategorie auf. Die Zahl der Beobachtungen in einer Kategorie ist die beobachtete Häufigkeit n_j.

Man überlegt sich nun, wie viele Beobachtungen im Mittel in einer Kategorie liegen müssten, wenn x tatsächlich die hypothetische Verteilung hat. Dazu berechnet man zunächst die Wahrscheinlichkeit F_o(x)_j, dass x in diese Kategorie fällt.

$n_{jo}=F_o(x)_j\cdot n$

ist die unter H₀ zu erwartende Häufigkeit.

Die Prüfgröße für den Test ist

$\chi ^2= \sum_{j=1}^m \frac{(n_j-n_{jo})^2}{n_{jo}}$ .

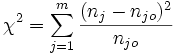Die Prüfgröße χ² ist bei ausreichend großen n_j annähernd χ²-verteilt mit m-1 Freiheitsgraden.

Wenn die Nullhypothese wahr ist, sollte der Unterschied zwischen der beobachteten und der theoretisch erwarteten Häufigkeit klein sein. Also wird H₀ bei einem hohen Prüfgrößenwert abgelehnt, der Ablehnungsbereich für H₀ liegt rechts.

Bei einem Signifikanzniveau α wird H₀ abgelehnt, wenn χ² > χ²(1-α; m-1), dem (1-α)-Quantil der χ²-Verteilung mit m-1 Freiheitsgraden ist.

Es existieren Tabellen für die χ²-Schwellenwerte in Abhängigkeit von der Anzahl der Freiheitsgrade und vom gewünschten Signifikanzniveau, z. B. [1] oder (knapper) [2].

Soll die Sicherheitsschwelle (= Signifikanzniveau), die zu einem bestimmten χ² gehört, bestimmt werden, so muss in der Regel aus der Tabelle ein Zwischenwert berechnet werden. Dazu verwendet man logarithmische Interpolation.

Besonderheiten

Schätzung von Verteilungsparametern

Im allgemeinen gibt man bei der Verteilungshypothese die Parameter der Verteilung an. Kann man diese nicht angeben, müssen sie aus der Stichprobe geschätzt werden. Hier geht bei der χ²-Verteilung pro geschätztem Parameter ein Freiheitsgrad verloren. Sie hat also m-w-1 Freiheitsgrade mit w als Zahl der geschätzten Parameter.

Mindestgröße der erwarteten Häufigkeiten

Damit die Prüfgröße als annähernd χ²-verteilt betrachtet werden kann, muss jede erwartete Häufigkeit eine gewisse Mindestgröße betragen. Verschiedene Lehrwerke setzen diese bei 1 oder 5 an. Ist die erwartete Häufigkeit zu klein, können gegebenenfalls mehrere Klassen zusammengefasst werden, um die Mindestgröße zu erreichen.

Beispiel zu Anpassungstest

Es liegen von ca. 200 börsennotierten Unternehmen die Umsätze vor. Das folgende Histogramm zeigt ihre Verteilung.

Es sei x: Umsatz eines Unternehmens [Mio. €].

Es soll nun die Hypothese getestet werden, dass x normalverteilt ist.

Da die Daten in vielen verschiedenen Ausprägungen vorliegen, wurden sie in Klassen eingeteilt. Es ergab sich die Tabelle:

Klasse	Intervall		Beobachtete Häufigkeit
j	über	bis	nj
1	…	0	0
2	0	5000	148
3	5000	10000	17
4	10000	15000	5
5	15000	20000	8
6	20000	25000	4
7	25000	30000	3
8	30000	35000	3
9	35000	...	9
Summe			197

Da keine Parameter vorgegeben werden, werden sie aus der Stichprobe ermittelt. Es sind geschätzt

$\hat \mu = \bar x = 6892$

und

$\hat \sigma = s = 14984.$

Es wird getestet:

H₀: X ist normalverteilt mit dem Erwartungswert μ = 6892 und der Varianz σ² = 14984².

Um die erwarteten Häufigkeiten zu bestimmen, werden zunächst die Wahrscheinlichkeit berechnet, dass X in die vorgegebenen Klassen fällt. Es sei Φ(x|6892;14984²) die Verteilungsfunktion der oben angegebenen Normalverteilung an der Stelle x. Man errechnet dann

$P(X \le 0) = F_{1o} = \Phi(0|6892;14984^2) = 0{,}3228$

$P(0 < X \le 5000) = \Phi(5000|6892;14984^2) - \Phi(0|6892;14984^2) = 0{,}1270$

…

Daraus ergeben sich die erwarteten Häufigkeiten

$n_{1o} = n \cdot F_{1o} = 197 \cdot 0{,}3228 = 63{,}59$

$n_{2o} = 197 \cdot 0{,}1270 = 25{,}02$

…

Es müssten also beispielsweise ca. 25 Unternehmen im Mittel einen Umsatz zwischen 0 und 5000 € haben, wenn das Merkmal Umsatz tatsächlich normalverteilt ist.

Die erwarteten Häufigkeiten sind zusammen mit den beobachteten Häufigkeiten in der folgenden Tabelle aufgeführt.

Klasse	Intervall		Beobachtete Häufigkeit	Wahrscheinlichkeit	Erwartete Häufigkeit
j	über	bis	nj	Fjo	njo
1	…	0	0	0,3228	63,59
2	0	5000	148	0,1270	25,02
3	5000	10000	17	0,1324	26,08
4	10000	15000	5	0,1236	24,35
5	15000	20000	8	0,1034	20,36
6	20000	25000	4	0,0774	15,25
7	25000	30000	3	0,0519	10,23
8	30000	35000	3	0,0312	6,14
9	35000	…	9	0,0303	5,98
Summe			197	1,0000	197,00

Die Prüfgröße wird jetzt folgendermaßen ermittelt:

$\chi^2 = \frac{(0- 63,59)^2}{63{,}59} + \frac{(148 - 25{,}02)^2}{25{,}02} + \dots + \frac{(9 - 5{,}98)^2}{5{,}98} = 710{,}79 .$

Bei einem Signifikanzniveau α = 0,05 liegt der kritische Wert der Testprüfgröße bei χ²(0,95;9-3=6) = 12,59. Da χ² > 12,59 ist, wird die Hypothese abgelehnt. Man kann davon ausgehen, dass das Merkmal Umsatz nicht normalverteilt ist.

Ergänzung

Die Daten wurden logarithmiert. Ein Normalverteilungstest dieser Daten wurde bei einem Signifikanzniveau von 0,05 nicht abgelehnt.

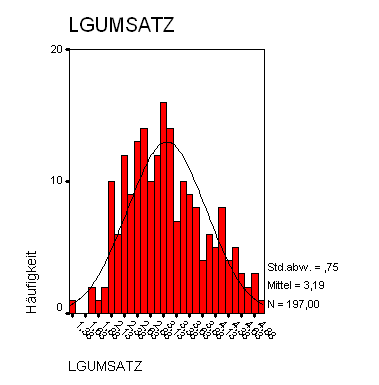
Das folgende Histogramm zeigt die Verteilung der logarithmierten Daten.

Unabhängigkeitstest

Siehe auch: Vierfeldertest

Der Unabhängigkeitstest ist ein Signifikanztest auf Unabhängigkeit in der Kontingenztafel.

Man betrachtet zwei statistische Merkmale x und y, die beliebig skaliert sein können. Man interessiert sich dafür, ob die Merkmale stochastisch unabhängig sind. Es wird die Nullhypothese

H₀: Das Merkmal x ist vom Merkmal y stochastisch unabhängig.

aufgestellt.

Vorgehensweise

Die Beobachtungen von x liegen in m Kategorien j (j = 1, …, m) vor, die des Merkmals y in r vielen Kategorien k (k = 1, …, r) vor. Treten bei einem Merkmal sehr viele Ausprägungen auf, fasst man sie zweckmäßigerweise zu Klassen j zusammen und fasst die Klassenzugehörigkeit als j-te Kategorie auf. Es gibt insgesamt n viele paarweise Beobachtungen von x und y, die sich auf m×r Kategorien verteilen.

Konzeptionell ist der Test so aufzufassen:

Man betrachte zwei diskrete Zufallsvariablen X und Y, deren gemeinsame Wahrscheinlichkeiten in einer Wahrscheinlichkeitstabelle dargestellt werden können.

Man zählt nun, wie oft die j-te Ausprägung von X zusammen mit der k-ten Ausprägung von Y auftritt. Die beobachteten gemeinsamen absoluten Häufigkeiten n_jk können in einer zweidimensionalen Häufigkeitstabelle mit m Zeilen und r Spalten eingetragen werden.

	Merkmal y						Σ
Merkmal x	1	2	…	k	…	r	nj.
1	n11	n12	...	n1k	...	n1r	n1.
2	n21	n22	…	n2k	…	n2r	n2.
…	…	…	…	…	…	…	…
j	…	…	…	njk	…	…	…
…	…	…	…	…	…	…	…
m	nm1	nm2	…	nmk	…	nmr	nm.
Σ	n.1	n.2	…	n.k	…	n.r	n

Die Zeilen- bzw. Spaltensummen ergeben die absoluten Randhäufigkeiten n_j. bzw. n_.k als

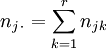$n_{j\,\cdot }= \sum_{k=1}^r n_{jk}$ und $n_{\cdot\, k}= \sum_{j=1}^m n_{jk}$

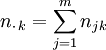
Entsprechend sind die gemeinsamen relative Häufigkeiten p_jk = n_jk/n und die relativen Randhäufigkeiten p_j. = n_j./n und p._k = n._k/n .

Wahrscheinlichkeitstheoretisch gilt: Sind zwei Ereignisse A und B stochastisch unabhängig, ist die Wahrscheinlichkeit für ihr gemeinsames Auftreten gleich dem Produkt der Einzelwahrscheinlichkeiten:

$P(A\cap B)= P(A)\cdot P(B)$

Man überlegt sich nun, dass analog zu oben bei stochastischer Unabhängigkeit von x und y auch gelten müsste

$p_{jk}\approx p_{j\,\cdot}\cdot p_{\cdot\, k}$ ,

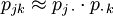mit n multipliziert entsprechend

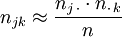$n_{jk}\approx \frac{n_{j\,\cdot}\cdot n_{\cdot\,k}}{n}$ oder auch

$n_{jk} - \frac{n_{j\,\cdot}\cdot n_{\cdot \,k}}{n}\approx 0$.

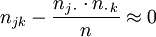Sind diese Differenzen für sämtliche j, k klein, kann man vermuten, dass x und y tatsächlich stochastisch unabhängig sind.

Setzt man für die erwartete Häufigkeit bei Vorliegen von Unabhängigkeit

$n^*_{jk}=\frac{n_{j\,\cdot}\cdot n_{\cdot \,k}}{n}$

resultiert aus der obigen Überlegung die Prüfgröße für den Unabhängigkeitstest

$\chi ^2= \sum_{j=1}^m\sum_{k=1}^r \frac{(n_{jk}- n^*_{jk})^2}{n^*_{jk}}$ .

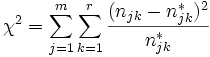Die Prüfgröße χ² ist bei ausreichend großen erwarteten Häufigkeiten n_jk* annähernd χ²-verteilt mit (m-1)(r-1) Freiheitsgraden.

Wenn die Prüfgröße klein ist, wird vermutet, dass die Hypothese wahr ist. Also wird H₀ bei einem hohen Prüfgrößenwert abgelehnt, der Ablehnungsbereich für H₀ liegt rechts.

Bei einem Signifikanzniveau α wird H₀ abgelehnt, wenn χ² > χ²(1-α; (m-1)(r-1)), dem (1-α)-Quantil der χ²-Verteilung mit (m-1)(r-1) Freiheitsgraden ist.

Besonderheiten

Damit die Prüfgröße als annähernd χ²-verteilt betrachtet werden kann, muss jede erwartete Häufigkeit eine gewisse Mindestgröße betragen. Verschiedene Lehrwerke setzen diese bei 1 oder 5 an. Ist die erwartete Häufigkeit zu klein, können gegebenenfalls mehrere Klassen zusammengefasst werden, um die Mindestgröße zu erreichen.

Beispiel zu Unabhängigkeitstest

Im Rahmen des Qualitätsmanagements wurden die Kunden einer Bank befragt, unter anderem nach ihrer Zufriedenheit mit der Geschäftsabwicklung und nach der Gesamtzufriedenheit. Der Grad der Zufriedenheit richtete sich nach dem Schulnotensystem.

Aus den Daten ergibt sich die folgende Kreuztabelle der Gesamtzufriedenheit von Bankkunden versus ihrer Zufriedenheit mit der Geschäftsabwicklung. Man sieht, dass einige erwartete Häufigkeiten zu klein waren.

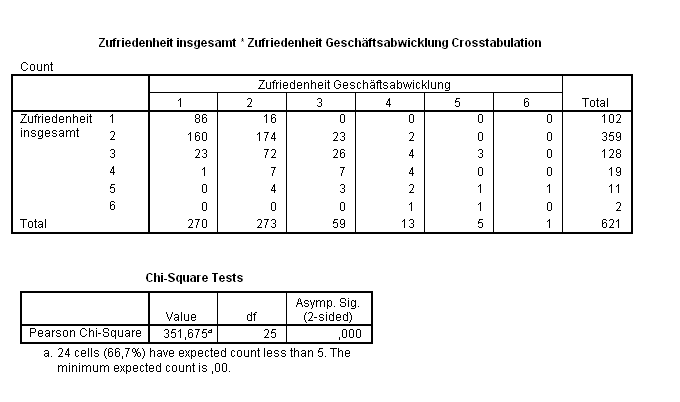
Eine Reduzierung der Kategorien auf jeweils drei ergab methodisch korrekte Ergebnisse.

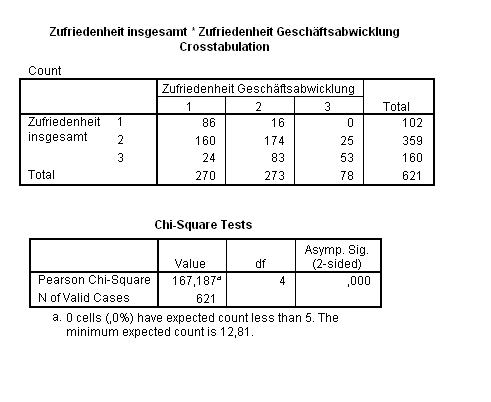
Die folgende Tabelle enthält die erwarteten Häufigkeiten n_jk*, die sich so berechnen:

$n^*_{11}= \frac{102 \cdot 270}{621} = 44{,}35 \quad n^*_{12} = \frac{102 \cdot 273}{621}= 44{,}84 \quad \dots \quad n^*_{33}= \frac{160 \cdot 78}{621} = 20{,}10$

	Merkmal y
Merkmal x	1	2	3	Σ
1	44,35	44,84	12,81	102
2	156,09	157,82	45,09	359
3	69,57	70,34	20,10	160
Σ	270	273	78	621

Die Prüfgröße wird dann folgendermaßen ermittelt:

$\chi^2 = \frac{(86 - 44{,}35)^2}{44{,}35} + \frac{(16 - 44{,}84)^2}{44{,}84} + \dots + \frac{(53 - 20{,}10)^2}{20{,}10} = 167{,}187$

Bei einem α = 0,05 liegt der kritische Wert der Testprüfgröße bei χ²(0,95; 4) = 9,488. Da χ² > 9,488 ist, wird die Hypothese signifikant abgelehnt, man vermutet also, dass die Gesamtzufriedenheit von der Zufriedenheit mit der Geschäftsabwicklung beeinflusst wurde.

Tabelle der Quantile der Chi-Quadrat-Verteilung

Die Tabelle zeigt die wichtigsten Quantile der Chi-Quadrat-Verteilung. In der linken Spalte sind die Freiheitsgrade und in der oberen Zeile die (1-alpha)-Niveaus eingetragen. Ablesebeispiel: Das Quantil der Chi-Quadrat-Verteilung bei 2 Freiheitsgraden und einem alpha-Niveau von 1% beträgt 9,21.

	1-α
f	0,900	0,950	0,975	0,990	0,995	0,999
1	2,71	3,84	5,02	6,63	7,88	10,83
2	4,61	5,99	7,38	9,21	10,60	13,82
3	6,25	7,81	9,35	11,34	12,84	16,27
4	7,78	9,49	11,14	13,28	14,86	18,47
5	9,24	11,07	12,83	15,09	16,75	20,52
6	10,64	12,59	14,45	16,81	18,55	22,46
7	12,02	14,07	16,01	18,48	20,28	24,32
8	13,36	15,51	17,53	20,09	21,95	26,12
9	14,68	16,92	19,02	21,67	23,59	27,88
10	15,99	18,31	20,48	23,21	25,19	29,59
11	17,28	19,68	21,92	24,72	26,76	31,26
12	18,55	21,03	23,34	26,22	28,30	32,91
13	19,81	22,36	24,74	27,69	29,82	34,53
14	21,06	23,68	26,12	29,14	31,32	36,12
15	22,31	25,00	27,49	30,58	32,80	37,70
16	23,54	26,30	28,85	32,00	34,27	39,25
17	24,77	27,59	30,19	33,41	35,72	40,79
18	25,99	28,87	31,53	34,81	37,16	42,31
19	27,20	30,14	32,85	36,19	38,58	43,82
20	28,41	31,41	34,17	37,57	40,00	45,31
21	29,62	32,67	35,48	38,93	41,40	46,80
22	30,81	33,92	36,78	40,29	42,80	48,27
23	32,01	35,17	38,08	41,64	44,18	49,73
24	33,20	36,42	39,36	42,98	45,56	51,18
25	34,38	37,65	40,65	44,31	46,93	52,62
26	35,56	38,89	41,92	45,64	48,29	54,05
27	36,74	40,11	43,19	46,96	49,64	55,48
28	37,92	41,34	44,46	48,28	50,99	56,89
29	39,09	42,56	45,72	49,59	52,34	58,30
30	40,26	43,77	46,98	50,89	53,67	59,70
40	51,81	55,76	59,34	63,69	66,77	73,40
50	63,17	67,50	71,42	76,15	79,49	86,66
60	74,40	79,08	83,30	88,38	91,95	99,61
70	85,53	90,53	95,02	100,43	104,21	112,32
80	96,58	101,88	106,63	112,33	116,32	124,84
90	107,57	113,15	118,14	124,12	128,30	137,21
100	118,50	124,34	129,56	135,81	140,17	149,45
200	226,02	233,99	241,06	249,45	255,26	267,54
300	331,79	341,40	349,87	359,91	366,84	381,43
400	436,65	447,63	457,31	468,72	476,61	493,13
500	540,93	553,13	563,85	576,49	585,21	603,45

Siehe auch

• Exakter Test nach Fisher
• Cramers V
• Kolmogorow-Smirnow-Test

Weblinks

• Exakte p-Werte