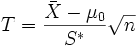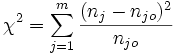Testgröße

Als Teststatistik (synonyme Begriffe: Testgröße, Prüfgröße, Prüffunktion) bezeichnet man in der mathematischen Statistik eine bestimmte Stichprobenfunktion, die bei einem Hypothesentest dazu verwendet wird, die Testentscheidung – also Ablehnen oder Nichtablehnen der Nullhypothese – zu treffen.

Verwendung bei festem Signifikanzniveau

Vor der Durchführung des Tests, das heißt auch vor der Ziehung der hierzu benötigten Stichprobe, ist die Teststatistik – üblicherweise mit T bezeichnet – eine Zufallsvariable, deren Wahrscheinlichkeitsverteilung von jener der Stichprobenvariablen X₁,X₂,...,X_n, mit n = Stichprobenumfang, abhängt. Unter der Annahme, dass die Nullhypothese (H₀) richtig ist, wird für die Verteilung der Teststatistik je nach Testverfahren ein bestimmtes Verteilungsmodell angenommen, dessen Verteilungsparameter sich aus der Nullhypothese ergeben. Anhand dieser angenommenen Verteilung sowie des zuvor festgelegten Signifikanzniveaus wird zugleich der Ablehnbereich bestimmt. Nun wird die Stichprobe gezogen und aus den sich dabei ergebenden Stichprobenwerten der konkrete Wert t der Teststatistik errechnet. Zur Ablehnung der Nullhypothese kommt es genau dann, wenn t in den Ablehnbereich fällt, anderenfalls wird unter dem verwendeten Signifikanzniveau die Nullhypothese beibehalten. Wenn nämlich die Nullhypothese gilt und damit die unterstellte Verteilung der Teststatistik als richtig angenommen werden kann, beträgt die Wahrscheinlichkeit, dass die Testgröße in den Ablehnbereich fällt und somit die Nullhypothese fälschlich abgelehnt wird (sogenannter Fehler 1. Art), genau dem festgelegten Signifikanzniveau. Das Fallen der Testgröße in den Ablehnbereich ist gleichbedeutend mit der (je nach Testproblem) Über- bzw. Unterschreitung eines bestimmten Schwellenwertes, der auch als „Kritischer Wert“ bezeichnet wird.

Verwendung mit p-Wert

Eine alternative, heutzutage in vielen statistischen Softwareanwendungen übliche Vorgehensweise besteht darin, anstatt sich vorher auf eine bestimmte Wahrscheinlichkeit für den Fehler 1. Art festzulegen, die Testentscheidung durch Berechnung des sogenannten p-Wertes zu treffen. In diesem Fall wird die Stichprobe ohne vorherige Festlegung des Signifikanzniveaus gezogen und der Wert t der Teststatistik anschließend berechnet. Je nachdem, in welchen Bereich der für T angenommenen Verteilung er fällt, ergibt sich ein p-Wert, der umso stärker die Ablehnung der Nullhypothese „signalisiert“, je kleiner er ist (aus diesem Grund interpretiert man den p-Wert auch als Maß für die „Signifikanz“ der Nullhypothese). Somit wird bei dieser Vorgehensweise, im Gegensatz zu der oben beschriebenen „klassischen“ Methode, nicht der Wert der Teststatistik selbst zur Testentscheidung herangezogen, sondern der aus ihm ermittelte p-Wert.

Beispiele für Teststatistiken

• Beim t-Test über einen Erwartungswert ist die Teststatistik wie folgt definiert:

$T=\frac{\bar{X}-\mu_{0}} {S^*} \sqrt{n}$

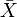mit $\bar{X}$ = Stichprobenmittelwert, μ₀ = laut Nullhypothese angenommener exakter Wert bzw. Obergrenze bzw. Untergrenze für den Erwartungswert μ, S* = korrigierte Stichprobenstandardabweichung.
Unter H₀ ist beim t-Test über einen Erwartungswert die Teststatistik t-verteilt mit n–1 Freiheitsgraden.

• Beim Chi-Quadrat-Anpassungstest lautet die Teststatistik:

$\chi ^2= \sum_{j=1}^m \frac{(n_j-n_{jo})^2}{n_{jo}}$

mit m = Anzahl der Ausprägungsklassen des betreffenden Merkmals, n_j = empirische (sich aus der Stichprobe ergebende) Häufigkeit des Auftretens des Merkmals in der j-ten Klasse, n_jo = theoretische (unter H₀ unterstellte) Häufigkeit des Auftretens des Merkmals in der j-ten Klasse.
Unter H₀ ist bei diesem Test die Testgröße annähernd Chi-Quadrat-verteilt mit m-1 Freiheitsgraden.