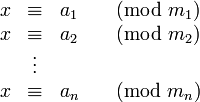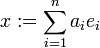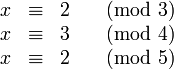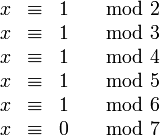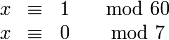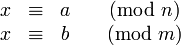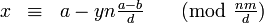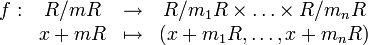Chinesischer Restklassensatz

Chinesischer Restsatz ist der Name mehrerer ähnlicher Theoreme der abstrakten Algebra und Zahlentheorie.

Simultane Kongruenzen ganzer Zahlen

Eine simultane Kongruenz ganzer Zahlen ist ein System von linearen Kongruenzen

$\begin{matrix} x & \equiv & a_1 & \pmod{m_1} \\ x & \equiv & a_2 & \pmod{m_2} \\ & \vdots & & \\ x & \equiv & a_n & \pmod{m_n} \\ \end{matrix}$

für die alle x bestimmt werden sollen, die sämtliche Kongruenzen gleichzeitig lösen. Wenn eine Lösung x existiert, dann sind mit M: = kgV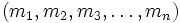$(m_1, m_2, m_3, \ldots, m_n)$ die Zahlen 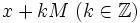$x + kM \ (k \in \mathbb{Z})$ genau alle Lösungen. Es kann aber auch sein, dass es gar keine Lösung gibt.

Teilerfremde Moduln

Die Originalform des Chinesischen Restsatzes stammt vom Mathematiker Sun Zi (3. Jhd.) und wurde 1247 von Ch'in Chiu-Shao wiederveröffentlicht. Der Satz trifft eine Aussage über simultane Kongruenzen für den Fall, dass die Moduln teilerfremd sind. Sie lautet:

Seien 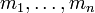$m_1, \ldots, m_n$ paarweise teilerfremde natürliche Zahlen, dann existiert für jedes Tupel ganzer Zahlen 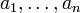$a_1, \ldots, a_n$ eine ganze Zahl x, die die folgende simultane Kongruenz erfüllt:

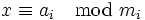$x \equiv a_i \mod m_i$ für $i = 1, \ldots, n$

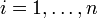
Alle Lösungen dieser Kongruenz sind kongruent modulo $M := m_1 m_2 m_3 \ldots m_n$.

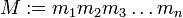Das Produkt M stimmt hier wegen der Teilerfremdheit mit dem kgV überein.

Finden einer Lösung

Eine Lösung x kann man wie folgt ermitteln. Für jedes i sind die Zahlen m_i und M_i: = M / m_i teilerfremd, also kann man z. B. mit dem erweiterten euklidischen Algorithmus zwei Zahlen r_i und s_i finden, so dass

$r_i \cdot m_i + s_i \cdot M_i = 1$.

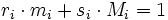Setzen wir 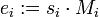$e_i := s_i \cdot M_i$, dann gilt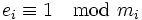

$e_i \equiv 1 \mod m_i$

$e_i \equiv 0 \mod m_j, \ j \neq i$.

Die Zahl

$x := \sum_{i=1}^n a_i e_i$

ist dann eine Lösung der simultanen Kongruenz.

Beispiel

Gesucht sei eine ganze Zahl x mit der Eigenschaft

$\begin{matrix} x & \equiv & 2 & \pmod 3 \\ x & \equiv & 3 & \pmod 4 \\ x & \equiv & 2 & \pmod 5 \\ \end{matrix}$

Hier ist 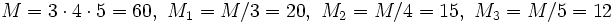$M = 3 \cdot 4 \cdot 5 = 60, \ M_1 = M/3 = 20, \ M_2 = M/4 = 15, \ M_3 = M/5 = 12$. Mit Hilfe des erweiterten euklidischen Algorithmus berechnet man

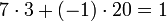$7 \cdot 3 + (-1) \cdot 20 = 1$, also e₁ = − 20

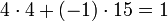$4 \cdot 4 + (-1) \cdot 15 = 1$, also e₂ = − 15

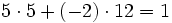$5 \cdot 5 + (-2) \cdot 12 = 1$, also e₃ = − 24

Eine Lösung ist dann 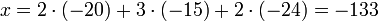$x = 2 \cdot (-20) + 3 \cdot (-15) + 2 \cdot (-24) = -133$. Wegen 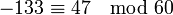$-133 \equiv 47 \mod 60$ sind alle anderen Lösungen also kongruent zu 47 modulo 60.

Allgemeiner Fall

Auch im Fall, dass die Moduln nicht teilerfremd sind, existiert manchmal eine Lösung. Die genaue Bedingung lautet: Eine Lösung der simultanen Kongruenz existiert genau dann, wenn für alle 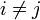$i \neq j$ gilt:

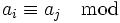$a_i \equiv a_j \mod$ ggT(m_i,m_j).

Alle Lösungen sind dann kongruent modulo dem kgV der m_i.

Eine simultane Kongruenz lässt sich im Falle der Existenz einer Lösung z.B. durch sukzessive Substitution lösen, auch wenn die Moduln nicht teilerfremd sind.

Beispiel

Ein klassisches Rätsel besteht darin, die kleinste natürliche Zahl zu finden, die bei Division durch 2, 3, 4, 5 und 6 jeweils den Rest 1 lässt, und durch 7 teilbar ist. Gesucht ist also die kleinste positive Lösung x der simultanen Kongruenz

$\begin{matrix} x & \equiv & 1 & \mod 2 \\ x & \equiv & 1 & \mod 3 \\ x & \equiv & 1 & \mod 4 \\ x & \equiv & 1 & \mod 5 \\ x & \equiv & 1 & \mod 6 \\ x & \equiv & 0 & \mod 7 \\ \end{matrix}$

Da die Moduln nicht teilerfremd sind, kann man nicht direkt den Chinesischen Restsatz (mit Lösungsverfahren) anwenden. Man kann aber die ersten fünf Bedingungen zusammenfassen zu 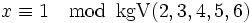$x \equiv 1 \mod \operatorname{kgV}(2, 3, 4, 5, 6)$, d.h. zu finden ist eine Lösung von

$\begin{matrix} x & \equiv & 1 & \mod 60 \\ x & \equiv & 0 & \mod 7 \\ \end{matrix}$

Dieses Kongruenzsystem ist nun mit dem Chinesischen Restsatz lösbar.

Direktes Lösen von simultanen Kongruenzen ganzer Zahlen

Gegeben sind die beiden simultanen Kongruenzen:

$\begin{matrix} x & \equiv & a & \pmod{n} \\ x & \equiv & b & \pmod{m} \\ \end{matrix}$

Wenn diese lösbar sind, das heißt 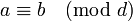$a \equiv b \pmod d$, so sind sie äquivalent mit der einfachen Kongruenz:

$\begin{matrix} x & \equiv & a - yn \frac{a-b}{d} & \pmod{ \frac{nm}{d}} \\ \end{matrix}$

mit d = ggT(n,m) = yn + zm.

Dieses funktioniert auch mit nicht teilerfremden Zahlen n und m und stellt somit eine deutliche Erleichterung bei dem Lösen von simultanen Kongruenzen dar.

Ein System aus Kongruenzen lässt sich durch wiederholtes Anwenden dieser Vereinfachung lösen.

Aussage für Hauptidealringe

Sei R ein Hauptidealring, dann lautet der Chinesische Restsatz für R so:

Sind 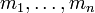$m_1, \ldots, m_n$ paarweise teilerfremd und m ihr Produkt, dann ist der Faktorring R / mR isomorph zum Produktring $R/m_1 R \times \ldots \times R/m_n R$ durch den Isomorphismus

$\begin{matrix} f : & R/mR & \to & R/m_1R \times \ldots \times R/m_nR \\ & x + mR & \mapsto & (x + m_1R, \ldots, x + m_nR) \end{matrix}$

Aussage für allgemeine Ringe

Eine der allgemeinsten Formen des Chinesischen Restsatzes ist eine Formulierung für einen beliebigen Ring R (mit Einselement).

Sind 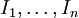$I_1, \ldots, I_n$ (beidseitige) Ideale, so dass I_i + I_j = R für 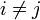$i \neq j$ (man nennt die Ideale dann teilerfremd oder komaximal), und sei I das Produkt der Ideale, dann ist I gleich dem Durchschnitt der I_j und der Faktorring R / I ist isomorph zum Produktring $R/I_1 \times \ldots \times R/I_n$ durch den Isomorphismus

$\begin{matrix} f : & R/I & \to & R/I_1 \times \ldots \times R/I_n \\ & x + I & \mapsto & (x + I_1, \ldots, x + I_n). \end{matrix}$

Weblinks

• Beweis des Satzes im Beweisarchiv
• [1] Tool zur Berechnung simultaner Kongruenzen