Clopen

Im Teilgebiet Topologie der Mathematik ist eine abgeschlossene offene Menge (im Englischen clopen set) eine Teilmenge eines topologischen Raums, die gleichzeitig abgeschlossen und offen ist.

Dies erscheint auf den ersten Blick seltsam; man muss aber bedenken, dass die Begriffe "offen" und "abgeschlossen" in der Topologie eine andere Bedeutung als in der Alltagssprache haben.

Beispiele

In jedem topologischen Raum sind die leere Menge und der ganze Raum abgeschlossen und offen.

Im topologischen Raum X, der aus der Vereinigung der beiden Intervalle [0,1] und [2,3] besteht, versehen mit der aus der Standardtopologie auf $\mathbb{R}$ induzierten Topologie, ist die Menge [0,1] abgeschlossen und offen. Dies ist typisch in dem Sinne, dass in einem topologischen Raum jede Zusammenhangskomponente eine abgeschlossene offene Menge bildet.

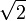Betrachte die Menge $\mathbb{Q}$ der rationalen Zahlen mit der Standardtopologie, und darin die Teilmenge A aller rationalen Zahlen, die größer als (oder hier äquivalent: mindestens so groß wie) die Quadratwurzel von 2 sind. Da $\sqrt{2}$ irrational ist, kann man leicht zeigen, dass A abgeschlossen und offen ist. Beachte aber, dass A als Teilmenge der reellen Zahlen weder abgeschlossen noch offen ist; die Menge aller reellen Zahlen größer als 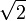$\sqrt{2}$ ist offen aber nicht abgeschlossen, während die Menge aller reellen Zahlen, die mindestens so groß wie 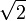$\sqrt{2}$ sind, abgeschlossen aber nicht offen ist.

Eigenschaften

Eine Teilmenge eines topologischen Raumes ist genau dann offen und abgeschlossen, wenn ihr Rand leer ist.

Ein topologischer Raum X ist genau dann zusammenhängend, wenn die einzigen abgeschlossenen offenen Mengen die leere Menge und X sind.

Jede abgeschlossene offene Teilmenge lässt sich als (möglicherweise unendliche) Vereinigung von Zusammenhangskomponenten darstellen.

Wenn jede Zusammenhangskomponente offen ist (was zum Beispiel dann der Fall ist, wenn X nur endlich viele Komponenten hat, oder wenn X lokal zusammenhängend ist), dann ist auch jede Vereinigung von Zusammenhangskomponenten abgeschlossen und offen.

Ein topologischer Raum ist genau dann diskret, wenn jede Teilmenge abgeschlossen und offen ist.

Eine offene Untergruppe einer topologischen Gruppe ist auch abgeschlossen. Eine abgeschlossene Untergruppe von endlichem Index ist auch offen.