- Completeness
-
Vollständigkeit ist eine Eigenschaft formaler Systeme bzw. Kalküle. Man unterscheidet semantische Vollständigkeit („Alles, was wahr ist, ist beweisbar.“), klassische Vollständigkeit („Eine der zwei Aussagen
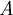 und
und 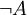 ist stets beweisbar.“) und syntaktische Vollständigkeit („Wird eine nicht beweisbare Aussage als Axiom verwendet, so ist die Widerspruchsfreiheit verletzt, d.h. alles wird beweisbar.“).
ist stets beweisbar.“) und syntaktische Vollständigkeit („Wird eine nicht beweisbare Aussage als Axiom verwendet, so ist die Widerspruchsfreiheit verletzt, d.h. alles wird beweisbar.“).Semantische Vollständigkeit ist das Pendant zur Korrektheit, in dem Sinn, dass ein Kalkül korrekt ist, wenn jede in ihm beweisbare (ableitbare) Aussage gilt („Alles, was beweisbar ist, ist wahr.“) Ein korrekter Kalkül ist insbesondere widerspruchsfrei, denn in einem Kalkül, der nicht widerspruchsfrei ist, d. h. in dem ein Widerspruch beweisbar ist, ist insbesondere alles, was falsch ist, beweisbar. Wenn ein Kalkül korrekt und vollständig ist, können in ihm genau alle wahren Aussagen abgeleitet werden.
Kurt Gödel bewies, dass die Prädikatenlogik erster Stufe nicht nur korrekt, sondern auch vollständig ist (Gödelscher Vollständigkeitssatz). Er bewies weiter, dass alle Systeme, die so mächtig sind wie die Arithmetik, entweder nicht vollständig oder nicht widerspruchsfrei sind, sowie dass sich Vollständigkeit und Widerspruchsfreiheit eines solchen Systems nicht innerhalb des Systems selbst beweisen lassen (siehe Gödelscher Unvollständigkeitssatz). Ähnliches folgt aus der von Alan Turing formal bewiesenen Unlösbarkeit des Halteproblems.
Funktionale Vollständigkeit von Junktoren
Mit funktionaler Vollständigkeit bezeichnet man die Eigenschaft einer Menge von Junktoren eines logischen Systems, alle Junktoren des Systems darstellen zu können. In der klassischen Aussagenlogik ist zum Beispiel die Junktorenmenge
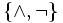 funktional vollständig, d. h. es lassen sich alle denkbaren Junktoren alleine aus Konjunktion und Negation ausdrücken.
funktional vollständig, d. h. es lassen sich alle denkbaren Junktoren alleine aus Konjunktion und Negation ausdrücken.
Wikimedia Foundation.
