Dicht (Topologie)

Der Begriff der dichten Teilmenge eines metrischen oder topologischen Raumes ist ein mathematischer Fachbegriff und wird in seiner allgemeinen Form im mathematischen Fachgebiet Topologie definiert. Er wird in vielen Teildisziplinen der Mathematik, etwa der Analysis, der Funktionalanalysis und der Numerik angewandt, zum Beispiel bei der Approximation von stetigen Funktionen durch Polynome.

Man sagt von einer Teilmenge, sie liege dicht in einem metrischen Raum, wenn man jeden Punkt des Gesamtraums beliebig genau durch einen Punkt aus der Teilmenge approximieren kann. So bilden die rationalen Zahlen $\Bbb{Q}$ eine dichte Teilmenge in der Menge der reellen Zahlen $\Bbb{R}$. Das bedeutet, dass man irrationale Zahlen beliebig genau durch rationale Brüche beziehungsweise durch endliche Dezimalzahlen approximieren kann. Allgemeiner sagt man von einer Teilmenge A, sie liege dicht in einem topologischen Raum X, wenn jede Umgebung eines beliebigen Punktes x aus X immer auch ein Element aus A enthält.

Ein Spezialfall dieses topologischen Begriffes „dicht“ ergibt sich durch die Anwendung auf geordnete Mengen. Eine Teilmenge S einer streng totalgeordneten Menge (M, < ) heißt dicht (in M), wenn es zu allen x und y aus M mit x < y ein z aus S gibt, so dass x < z < y. Dieser Spezialfall ergibt sich durch die Ordnungstopologie auf M und wird dort näher erläutert. Der vorliegende Artikel behandelt den allgemeineren topologischen Begriff.

Definition

Sei (X,T) ein topologischer Raum. Eine Teilmenge M liegt dicht in X genau dann, wenn eine der folgenden gleichwertigen Aussagen zutrifft:

• Der Abschluss von M stimmt mit X überein.
• Es gibt keine abgeschlossene Teilmenge von X außer X selbst, die M enthält.
• Jede Umgebung in X enthält einen Punkt aus M.

Beispiele (Topologie)

• Die Menge der rationalen Zahlen $\Bbb{Q}$ liegt dicht in der Menge der reellen Zahlen $\Bbb{R}$.
• Die Menge der irrationalen Zahlen liegt dicht in der Menge der reellen Zahlen $\Bbb{R}$.
• Die Menge der Polynome liegt dicht in der Menge der stetigen Funktionen auf einem kompakten Intervall.
• Die Menge der Testfunktionen liegt dicht in der Menge der Lebesgue-Integrierbaren Funktionen.
• Sei M eine Teilmenge eines mittels $\|\cdot\|$ normierten Raums X. Bezeichnet man mit 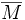$\overline{M}$ die abgeschlossene Hülle dieser Menge bezüglich der Norm $\|\cdot\|$, so liegt M dicht in $\overline{M}$.
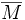• Die Menge der natürlichen Zahlen $\Bbb{N}$ liegt nicht dicht in der Menge der rationalen Zahlen $\Bbb{Q}$.

Zusammenhang mit anderen Begriffen

Ein Raum, der eine abzählbare dichte Teilmenge besitzt heißt separabel.

Ein komplementäres Konzept ist das der nirgends dichten Mengen, deren Abschluss ein leeres Inneres hat. Ein weiteres verwandtes Konzept ist die Unterscheidung von fetten und mageren Mengen.

Literatur

• Boto von Querenburg: Mengentheoretische Topologie. 3. Auflage. Springer-Verlag, 2001, ISBN 3-540-09799-6.
• Thorsten Camps, Stefan Kühling und Gerhard Rosenberger: Einführung in die mengentheoretische und die algebraische Topologie. Heldermann, 2006, ISBN 3-88538-115-X.