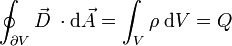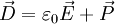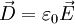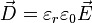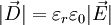Dielektrisches Verschiebungsfeld

Die elektrische Flussdichte - historische Bezeichnungen dafür sind auch dielektrische Verschiebung, elektrische Erregung oder Verschiebungsdichte - mit dem Formelzeichen 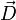$\vec{D}$ ist eine physikalische Größe in der Elektrostatik und Elektrodynamik.

Die (SI-abgeleitete) Einheit von D ist Coulomb/Quadratmeter (C/m²), also A·s/m². Ihre Einheit stimmt also mit der Einheit der Oberflächenladungsdichte σ überein, doch ist die elektrische Flussdichte anders als die Flächenladungsdichte eine vektorielle Größe. Die elektrische Flussdichte ist eine Feldgröße.

Herrscht zwischen zwei Punkten P₁ und P₂ im Raum eine elektrische Spannung, so spricht man von unterschiedlichen Potentialen in P₁ und P₂. Dazwischen liegen so genannte Äquipotentialflächen. Dies sind geschlossene Flächen mit jeweils konstantem Potential. Im rechten Winkel zu diesen Äquipotentialflächen stehen die elektrischen Flusslinien. Per Definition sind die positiven Ladungen die Quelle des elektrischen Flusses, die negativen Ladungen sind die Senke.

Der elektrische Fluss Ψ, der durch eine beliebige Fläche A hindurchtritt, ist gleich dem Flächenintegral der elektrischen Flussdichte D. Dabei trägt nur jener elektrische Flussanteil, der normal zur Fläche A steht, zum elektrischen Fluss durch die Fläche A bei. Mathematisch wird dieser Umstand mittels Vektoren und durch die Operation des Skalarprodukts (inneren Produkts) ausgedrückt als:

$\mathit{\Psi} = \int \limits_A \vec{D} \cdot \mathrm{d} \vec{A}$

Der elektrische Fluss durch eine geschlossene Fläche ist somit gleich der von dieser Fläche eingeschlossenen elektrischen Ladung.

$\oint_{\partial V} \vec{D}\;\cdot\mathrm{d}\vec{A} = \int_V\rho\;\mathrm{d}V = Q$

Die zeitliche Änderung der elektrischen Flussdichte steht als maxwellscher Verschiebungsstrom im erweiterten ampèreschen Gesetz.

Zusammenhang mit der elektrischen Feldstärke

Die elektrische Flussdichte lässt sich allgemein als Summe der Polarisation 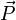$\vec{P}$ und des Produktes der elektrischen Feldstärke 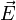$\vec{E}$ mit der elektrischen Feldkonstante (Dielektrizitätskonstante/Permittivität des Vakuums) 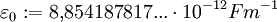$\varepsilon_0 := 8{,}854187817... \cdot 10^{-12} Fm^{-1}$ schreiben, also:

$\vec{D} = \varepsilon_0 \vec{E} + \vec{P}$

Im Fall des Vakuums verschwindet die Polarisation, daher steht die elektrische Flussdichte in einem einfachen Zusammenhang mit der elektrischen Feldstärke, nämlich:

$\vec{D} = \varepsilon_0 \vec{E}$

Im einfachsten Fall eines linearen, isotropen Mediums verändert sich der Zusammenhang zwischen der elektrischen Flussdichte und der elektrischen Feldstärke um die relative Permittivität 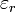$\varepsilon_r$ des Dielektrikums in dem die elektrische Flussdichte gemessen wird, so dass sich als Zusammenhang ergibt:

$\vec{D} = \varepsilon_r \varepsilon_0 \vec{E}$

Im Fall eines anisotropen Mediums zeigt die elektrische Flussdichte nicht mehr notwendigerweise in Richtung der elektrischen Feldstärke. Hängen die beiden Größen linear zusammen, so lässt sich ein Tensor 2.Stufe als eindeutiger Proportionalitätsfaktor angeben.

$\vec{D} = \begin{pmatrix} \varepsilon_{11} & \varepsilon_{12} & \varepsilon_{13} \\ \varepsilon_{21} & \varepsilon_{22} & \varepsilon_{23} \\ \varepsilon_{31} & \varepsilon_{32} & \varepsilon_{33} \end{pmatrix} \varepsilon_0 \vec{E}$

Eine Folge eines solchen Zusammenhangs ist die Doppelbrechung. Einkristalle zeigen typischerweise linear-anisotropes Verhalten. Ein Beispiel für nichtlineares Verhalten zwischen elektrischem Feld und Fluss stellen Ferroelektrika dar, die nach dem Anlegen eines hohen Feldes einen Teil ihrer Polarisation behalten.

Weitere Beispiele nichtlinearen Zusammenhanges zwischen elektrischer Flussdichte und elektrischer Feldstärke findet man in der nichtlinearen Optik.

Elektrische Flussdichte im Plattenkondensator

Im Plattenkondensator mit parallelen Platten zeigt die elektrische Flussdichte in Richtung der Flächennormale der Kondensatorplatten. Ihr Betrag ist dabei:

$|\vec{D}| = \frac{Q}{A}$.

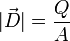Dabei ist Q die Ladungsmenge eines Plattenkondensators und A die Fläche der betreffenden Platten. Alternativ lässt sich das wegen E (elektrische Feldstärke) proportional zur Flächenladungsdichte (E~σ) schreiben als

$|\vec{D}| = \varepsilon_r \varepsilon_0 |\vec{E}|$

Siehe auch

• Elektrische Suszeptibilität
• Verschiebungsstrom