- Diskretes System
-
Bei kontinuierlichen dynamischen Systemen betrachtet man eine stetige Zeitachse
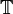 , wie z. B.
, wie z. B. 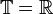 . Lässt man nur diskrete Zeiten zu wie
. Lässt man nur diskrete Zeiten zu wie 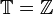 , so spricht man von einem diskreten dynamischen System. Diese Diskretisierung findet zum einen in der Numerik eine große Anwendung, wie z. B. bei der Rückwärtsanalyse. Zum Anderen existieren natürliche und technische Systeme, die durch nichtkontinuierliche Zusandsänderungen charakterisiert werden und in direkter Weise durch diskrete Dynamische Systeme modelliert werden können.
, so spricht man von einem diskreten dynamischen System. Diese Diskretisierung findet zum einen in der Numerik eine große Anwendung, wie z. B. bei der Rückwärtsanalyse. Zum Anderen existieren natürliche und technische Systeme, die durch nichtkontinuierliche Zusandsänderungen charakterisiert werden und in direkter Weise durch diskrete Dynamische Systeme modelliert werden können.
Es sei ein metrischer Raum X vorgegeben.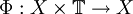 sei eine stetige Abbildung
sei eine stetige Abbildung 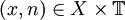 . Ein diskretes dynamisches System (oder auch diskreter Fluss) ist ein Tripel
. Ein diskretes dynamisches System (oder auch diskreter Fluss) ist ein Tripel 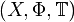 und besitzt die Eigenschaften:
und besitzt die Eigenschaften:(1) Φ(x,0) = Φ0(x) = x für alle

(2)
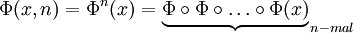 für alle
für alle  und
und 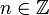 .
.Unter (1) versteht man die Identitätseigenschaft, d. h. ein Zustand verändert sich nicht nach 0 Zeiteinheiten. (2) gibt die Halbgruppeneigenschaft wieder.
Ist
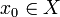 der Anfangszustand, x1 = Φ(x0) der Zustand zum Zeitpunkt t=1 usw. und xn der Zustand zum Zeitpunkt
der Anfangszustand, x1 = Φ(x0) der Zustand zum Zeitpunkt t=1 usw. und xn der Zustand zum Zeitpunkt 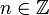 , so beschreibt xn + 1 = Φ(xn) die Dynamik des diskreten Systems.
, so beschreibt xn + 1 = Φ(xn) die Dynamik des diskreten Systems.Wie bei dynamischen Systemen interessiert man sich bei der Untersuchung von diskreten Systemen für Fixpunkte oder allgemeiner für Limesmengen und deren Stabilität. In chaotischen Abbildungen, wie z. B. der Bernoulli-Abbildung, logistischen Abbildung oder Hénon-Abbildung, spielen Diskretisierungen eine große Rolle, um die iterierten Abbildungen diskutieren zu können.
Wikimedia Foundation.
