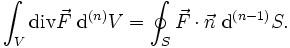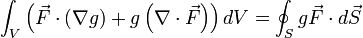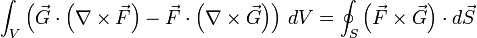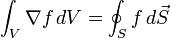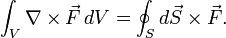Divergenzsatz

Der gaußsche Integralsatz, auch Satz von Gauß-Ostrogradski, Satz von Gauß oder Divergenzsatz, ist ein Ergebnis aus der Vektoranalysis. Er stellt einen Zusammenhang zwischen der Divergenz eines Vektorfeldes und dem durch das Feld vorgegebenen Fluss durch eine geschlossene Oberfläche her.

Der gaußsche Integralsatz folgt als Spezialfall aus dem Satz von Stokes, der wiederum den Hauptsatz der Differential- und Integralrechnung verallgemeinert.

Formulierung des Satzes

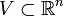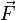Es sei: $V \subset \mathbb{R}^n$ kompakt mit abschnittsweise glattem Rand S, der Rand sei orientiert durch ein äußeres Normalen-Einheitsfeld $\vec n$. Ferner besitze das Vektorfeld $\vec F$ die Eigenschaft, dass 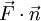$\vec F\cdot \vec n$ auf S integrierbar sei (z. B. stückweise stetig). Das gleiche gelte für 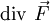${\rm div}\,\,\vec F$ im Innern von V. Dann gilt, mit den entsprechenden Volumen- bzw. Oberflächen-Inhalten, die folgende Beziehung:

$\int_V \operatorname{div} \vec F \; \mathrm d^{(n)}V = \oint_{S} \vec F \cdot \vec n\; \mathrm d^{(n-1)}S.$

Varianten

Aus dem gaußschem Integralsatz können weitere Identitäten hergeleitet werden.

• Wendet man den gaußschen Integralsatz auf das Produkt einer skalaren Funktion g mit einem Vektorfeld 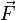$\vec F$ an, dann erhält man

$\int_V\left(\vec{F}\cdot \left(\nabla g\right) + g \left(\nabla\cdot \vec{F}\right)\right) dV = \oint_{S}g \vec{F} \cdot d\vec{S}$

Setzt man nun 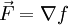$\vec{F}=\nabla f$, dann erhält man die Greenschen Formeln.

• Wendet man den gaußschen Integralsatz auf das Kreuzprodukt zweier Vektorfelder 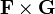$\mathbf{F}\times \mathbf{G}$ an, dann erhält man

$\int_V \left(\vec{G}\cdot\left(\nabla\times\vec{F}\right) - \vec{F}\cdot \left( \nabla\times\vec{G}\right)\right)\, dV = \oint_{S}\left(\vec{F}\times\vec{G}\right)\cdot d\vec{S}$

• Wendet man den gaußschen Integralsatz auf das Produkt einer skalaren Funktion f mit einem konstantem Vektor an, dann erhält man die folgende Identität:

$\int_V \nabla f\, dV = \oint_{S} f \,d\vec{S}$

• Wendet man den gaußschen Integralsatz auf das Kreuzprodukt eines Vektorfeldes 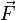$\vec F$ mit einem konstanten Vektor, dann lässt sich die folgende Identität zeigen:

$\int_V \nabla\times\vec{F}\, dV = \oint_{S}d\vec{S} \times\vec{F}.$

Anwendungen

Flüssigkeiten, Gase, Elektrodynamik

Der Satz wird genutzt zur Beschreibung der Erhaltung von Masse, Impuls und Energie in einem beliebigen Volumen: Das Integral der Quellenverteilung (Summe der Divergenz eines Vektorfeldes) über das Volumen im Innern einer Hülle multipliziert mit einer Konstanten ergibt den gesamten Durchfluss (das Hüllenintegral) der gesamten Strömung durch die Hülle dieses Volumens.

Gravitation

Im Gravitationsfeld erhält man: Das Oberflächenintegral ist -4πG mal die Masse innen, solange die Masse darin radialsymmetrisch verteilt ist (konstante Dichte bei gegebener Entfernung vom Mittelpunkt) und unabhängig von irgendwelchen (ebenfalls radialsymmetrisch verteilten) Massen außerhalb. Insbesondere gilt: Die ganze Sphäre außerhalb einer Kugel hat keinen (zusätzlichen) Einfluss, sofern ihre Masse radialsymmetrisch verteilt ist. Allein die Summe der Quellen und Senken im Innengebiet wirken.

Bedeutung

Der gaußsche Integralsatz findet in vielen Bereichen der Physik Anwendung, vor allem auch in der Elektrodynamik und der Fluiddynamik.

Im letzteren Fall wird die Bedeutung des Satzes besonders anschaulich. Nehmen wir an, das Vektorfeld 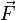$\vec F$ beschreibt fließendes Wasser in einem gewissen Raumbereich. Dann beschreibt die Divergenz von 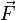$\vec F$ gerade die Stärke von allen Quellen und Senken in einzelnen Punkten. Möchte man nun wissen, wie viel Wasser aus einem bestimmten Bereich V insgesamt herausfließt, so ist intuitiv klar, dass man folgende zwei Möglichkeiten hat:

• Man untersucht bzw. misst, wie viel Wasser durch die Oberfläche von V aus- und eintritt. Dies entspricht dem Durchfluss von senkrechten Komponenten auf der Oberfläche als Oberflächenintegral.
• Man bilanziert (misst) im Innern des dadurch begrenzten Volumens, wie viel Wasser insgesamt innerhalb von V in Senken (Löchern) verschwindet und wie viel aus Quellen (Wasserzuflüssen) hinzukommt. Man addiert also die Effekte von Quellen und Senken. Dies wird alternativ und gleichwertig dann durch das Volumenintegral über die Divergenz realisiert.

Der gaußsche Integralsatz besagt, dass tatsächlich beide Möglichkeiten stets absolut gleichwertig zum Ziel führen. Er hat damit auch den Charakter eines Erhaltungssatzes der Energie, ist also der bekannte Energieerhaltungssatz.

Ein bildhaftes Anwendungsbeispiel des gaußschen Integralsatzes ist der mathematisch versierte Jäger auf einer Wildschweinjagd: Um festzustellen, ob sich in einem freistehenden Wäldchen noch Wildschweine befinden, wird er nicht in das Wäldchen hineinlaufen und die Tiere aufscheuchen, sondern er zählt die herausführenden und die hineinführenden Spuren. Vorausgesetzt wir haben mit fehlenden alten Spuren eine „Wildschweinquellfreiheit“ im Gebiet (Unterraum) „Wäldchen“ sichergestellt, dann weiß er durch Differenzbildung, wie viele Wildschweine sich noch in dem Wäldchen befinden.

Geschichte

Der Satz wurde wahrscheinlich zum ersten Mal von Joseph Louis Lagrange im Jahre 1762 formuliert und unabhängig davon später von Carl Friedrich Gauß (1813), George Green (1825) und Michail Ostrogradski (1831) neu entdeckt. Ostrogradski lieferte auch den ersten formalen Beweis.

Literatur

• Otto Forster: Analysis 3. Integralrechnung im Rⁿ mit Anwendungen. 3. Aufl. Vieweg-Verlag, 1996. ISBN 3-528-27252-X
• Konrad Königsberger: Analysis 2, Springer, Berlin 2004.