Affiner Teilraum

Der affine Raum nimmt im systematischen Aufbau der Geometrie eine Mittelstellung zwischen Euklidischem Raum und Projektivem Raum ein.

Informelle Definitionen

Der affine Raum (=lineare Mannigfaltigkeit) im engsten Sinne ist ein mathematisches Modell für den uns vertrauten dreidimensionalen Anschauungsraum.

In einem weiteren Sinne kann ein affiner Raum, wie andere mathematische Räume auch, eine beliebige Dimension haben: Als affinen Raum kann man auch einen einzelnen Punkt, die affine Gerade, die affine Ebene sowie vier- und höherdimensionale Räume bezeichnen.

Verschiedene mathematische Disziplinen haben unterschiedliche Präzisierungen dieses Begriffs gefunden.

Definition der synthetischen Geometrie

Ein affiner Raum im Sinne der synthetischen Geometrie besteht aus den folgenden Daten:

• einer Menge von Punkten
• einer Menge von Geraden
• einer Inzidenzrelation, die angibt, welche Punkte auf welchen Geraden liegen
• einer Parallelitätsrelation, die angibt, welche Geraden parallel sind,

so dass gewisse Axiome erfüllt sind, die die Anschauung nahelegt, unter anderem Euklids berühmtes Parallelenaxiom. Für weitere Details siehe affine Geometrie.

Alternativ dazu wird die affine Geometrie im Sinne des Erlanger Programms von Felix Klein als Inbegriff der unter affinen Transformationen invarianten geometrischen Eigenschaften eingeführt.

Definition der linearen Algebra

Gegeben seien eine Menge A, deren Elemente geometrisch als Punkte aufgefasst werden, ein Vektorraum V und eine Abbildung von 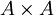$A \times A$ nach V, die zwei Punkten 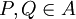$P, Q \in A$ einen Verbindungsvektor 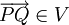$\overrightarrow{PQ} \in V$ zuordnet, so dass gilt:

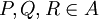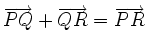• für alle $P, Q, R \in A$ gilt: $\overrightarrow{PQ}+\overrightarrow{QR}=\overrightarrow{PR}$ (Beziehung von Chasles),
• für alle 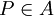$P \in A$ und alle 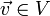$\vec{v}\in V$ gibt es einen eindeutigen Punkt 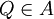$Q \in A$, so dass $\vec{v}=\overrightarrow{PQ}$.

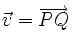Das Paar (A, V) heißt affiner Raum; wenn klar ist, welcher Vektorraum V zugrunde liegt, bezeichnet man auch A alleine als den affinen Raum.

Im affinen Raum ist eine Addition oder Translation als Abbildung von 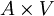$A \times V$ nach A dadurch definiert, dass 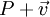$P + \vec{v}$ gerade der über 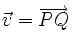$\vec{v}=\overrightarrow{PQ}$ eindeutig bestimmte Punkt Q ist.

Die Dimension des affinen Raums ist definiert als die Dimension des Vektorraums V.

Wenn P ein Punkt aus A ist und U ein Untervektorraum von V, dann ist (P+U, U) ein affiner Unterraum von (A, V). Anstelle des Begriffs Unter(vektor)raum wird auch oft die äquivalente Bezeichnung Teil(vektor)raum verwendet.

Affine Räume im Sinne der linearen Algebra sind auch affine Räume im Sinne der synthetischen Geometrie, jedoch nicht notwendigerweise umgekehrt, siehe Affine Geometrie.

Beispiele

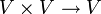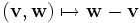• Jeder Vektorraum V ist in trivialer Weise ein affiner Raum über sich selbst, wenn man die Abbildung $V\times V\to V$ mit $(\mathbf{v},\mathbf{w})\mapsto \mathbf{w}-\mathbf{v}$ betrachtet.

• Der euklidische Raum Eⁿ ist der abstrakte affine Raum über dem Vektorraum $\mathbb{R}^n$.

• Die Lösungen eines inhomogenen linearen Gleichungssystems bilden einen affinen Raum über dem Vektorraum der Lösungen des zugehörigen homogenen Systems. Das gilt analog auch für Systeme linearer Differentialgleichungen.

• In der Differentialgeometrie spielen affine Räume eine Rolle in der Theorie der Faserbündel. Beispiele sind die Fasern des affinen Tangentialbündels, des Zusammenhangsbündel und von Jetbündeln.

Definition der algebraischen Geometrie

• In der klassischen algebraischen Geometrie ist der n-dimensionale affine Raum Aⁿ über einem algebraisch abgeschlossenen Körper k die algebraische Varietät kⁿ.

• In der modernen algebraischen Geometrie ist der n-dimensionale affine Raum Aⁿ_A über einem kommutativen Ring A mit Einselement definiert als das Spektrum des Polynomringes A[X₁,…,X_n] in n Unbestimmten.
  Für eine A-Algebra B sind die B-wertigen Punkte von Aⁿ_A gleich Bⁿ.

Siehe auch

• Affine Koordinaten

Weblinks

• Vorlesungsskript "Algebra und Geometrie" von Hubert Grassmann
• "Der affine Raum" mit Beispielen von Joachim Mohr